本文是从属于矢量分析的第二篇文章，在Vector analysis一文中我们比较详尽地介绍了包括矢量的乘积、矢量场的概念和性质定理等内容。但却只字未提矢量在空间中的坐标变换理论，矢量的坐标变换在知识体系框架是至关重要的一环，因此，本文从矢量的坐标变换理论展开叙述，本文与线性代数会产生些许联系噢。

$R^3$空间曲线坐标系中的向量分析

$R^3$空间中的曲线坐标系

• 在$R^3$空间中，我们选定坐标原点并建立笛卡尔坐标系，设笛卡尔坐标系的基向量为$(e_1,e_2,e_3)$，空间中任意一点的位矢均可以通过该基向量线性表出，即$\vec{r} = x_1e_1+x_2e_2+x_3e_3=\vec{r}(x_1,x_2,x_3)$。同一个空间的基向量有许多，因此我们也可以用另外一组基向量表征空间中的同一点，得到$r(u_1,u_2,u_3)$。我们要求同一点在两种不同基底下的坐标参数存在单值变换函数，即
  $$\begin{aligned}
  u_1=u^1(x_1,x_2,x_3)\\
  u_2=u^2(x_1,x_2,x_3)\\
  u_3=u^3(x_1,x_2,x_3)\\
  \end{aligned}$$
• 当上式方程组的值为常数时，我们就得到了用$(x_1,x_2,x_3)$表示的三个曲面，称为坐标曲面，这三个坐标曲面由下面的方程描述，其中$c_1,c_2,c_3$为常数
  $$\begin{aligned}
  u_1=u^1(x_1,x_2,x_3)=c_1\\
  u_2=u^2(x_1,x_2,x_3)=c_2\\
  u_3=u^3(x_1,x_2,x_3)=c_3\\
  \end{aligned}$$
• 每两个曲面相交得到的曲面称为坐标曲线，过三个空间的每一点都有三条坐标曲线，因此空间中的点都可以用参数$(u_1,u_2,u_3)$来描述，这样的坐标系称为曲线坐标系，参数$u_1,u_2,u_3$称为曲线坐标.如果三条坐标曲线两两正交，则称此曲线坐标系为正交曲线坐标系.
• 声明与强调：(务必要看这一点，不然下面的内容你大概率会十分疑惑大为不解然后弃之而去)
  • 上面和接下来的内容中$u_i,x_i,i=(1,2,3)$代表的是坐标参数，而$u^i,x^i$代表的是函数关系

曲线坐标系中的度量

• 1. 笛卡尔坐标系下线元的表示
  • 在$R_3$空间中的线元，即临近两点间线段长度的平方，在笛卡尔坐标系下表示为
    $$\begin{aligned}
    \mathrm{d}r^2 = \mathrm{d}\vec{r}\cdot\mathrm{d}\vec{r}= \mathrm{d}x_i\mathrm{d}x_i = \mathrm{d}x^2_1+\mathrm{d}x^2_2+\mathrm{d}x^2_3
    \end{aligned}$$
    因为是笛卡尔坐标系，这里的$(x_1,x_2,x_3)$对应为$(x,y,z)$
  • 上式的另一种表示为
    $$\begin{aligned}
    \mathrm{d}r^2 = \delta_{ij}\mathrm{d}x_i\mathrm{d}x_j
    \end{aligned}$$
    式中的$\delta_{ij}$称为$R^3$空间中的度量分量，其矩阵形式就是一个三阶单位阵
    $$(\delta_{ij})=\begin{pmatrix}
    1&0&0 \\
    0&1&0 \\
    0&0&1
    \end{pmatrix}$$
    上式的矩阵形式为
    $$ \mathrm{d}r^2=(\mathrm{d}x_1,\mathrm{d}x_2,\mathrm{d}x_3)\begin{pmatrix}
    1&0&0 \\
    0&1&0 \\
    0&0&1 \\
    \end{pmatrix}
    \begin{pmatrix}
    \mathrm{d}x_1 \\
    \mathrm{d}x_2 \\
    \mathrm{d}x_3
    \end{pmatrix}=\mathrm{d}x^2_1+\mathrm{d}x^2_2+\mathrm{d}x^2_3$$
• 2. 曲线坐标系下线元的表示
     根据笛卡尔坐标系与曲线坐标系下坐标的变换关系
     $$\begin{aligned}
     x_i =x^i(u_1,u_2,u_3)
     \end{aligned}$$
     由高等数学我们知道函数的全微分为
     $$\begin{aligned}
     \mathrm{d}x_i = \frac{\partial x^i}{\partial u_j}\mathrm{d}u_j
     \end{aligned}$$
     因此，根据线元表达式就可以得到
     $$\begin{aligned}
     \mathrm{d}r^2 =\frac{\partial x^i}{\partial u_j}\mathrm{d}u_j \frac{\partial x^i}{\partial u_k}\mathrm{d}u_k=\frac{\partial x^i}{\partial u_j}\frac{\partial x^i}{\partial u_k}\mathrm{d}u_j \mathrm{d}u_k
     \end{aligned}$$
• 定义：曲线坐标系下的度量系数$g_{ij}$
  $$\begin{aligned}
  g_{ij} = \frac{\partial x^k}{\partial u_i}\frac{\partial x^k}{\partial u_j}
  \end{aligned}$$
  则在$R^3$空间中的线元用曲线坐标系描述的表达式为
  $$\begin{aligned}
  \mathrm{d}r^2 = g_{ij}\mathrm{d}u_i\mathrm{d}u_j
  \end{aligned}$$
  • 在正交曲线坐标系有：
    $$g_{ij}=\begin{cases}
    g_{ij} \quad i=j \\
    0 \quad i\neq j
    \end{cases}$$
  • 在正交曲线坐标系下的线元表示为
    $$\begin{aligned}
    \mathrm{d}r^2 = g_{11}(\mathrm{d}u_1)^2+g_{22}(\mathrm{d}u_2)^2+g_{33}(\mathrm{d}u_3)^2
    \end{aligned}$$
  • 在正交曲线坐标系下，当线元只沿某一参量的方向变化时，就得到沿该参量方向的微小弧长变化，即
    $$\begin{aligned}
    \mathrm{d}s_i=\sqrt{g_{ii}}\mathrm{d}u_i\equiv h_i\mathrm{d}u_i \quad (i=1,2,3)
    \end{aligned}$$
    $h_i = \sqrt{g_{ii}}$ 称为度量分量
  • 据此，我们可以轻松的表示出曲线坐标系下面元和体积元的表示
    • $$\begin{aligned}
      \mathrm{d}\sigma_{ij} = h_1h_2\mathrm{d}u_1\mathrm{d}u_2
      \end{aligned}$$
    • $$\begin{aligned}
      \mathrm{d}V = h_1h_2h_3\mathrm{d}u_1\mathrm{d}u_2\mathrm{d}u_3
      \end{aligned}$$
• 笛卡尔坐标系与柱坐标系的变换
  • 笛卡尔坐标系参量(x,y,z)$\quad$柱坐标系参量($\rho,\varphi,z$)
  • 线元$\mathrm{d}r^2=\sum_{i=x,y,z}\mathrm{d}i\mathrm{d}i$
  • $\mathrm{d}i = \sum_{j=\rho,\varphi,z}\frac{\partial i}{\partial j}\mathrm{d}j$
  • 于是得到线元用柱坐标参量表征的结果为
    $$\begin{aligned}
    \mathrm{d}r^2 = \mathrm{d}\rho^2+\rho^2\mathrm{d}\varphi^2+\mathrm{d}z^2
    \end{aligned}$$
  • 于是我们得到了度量系数
    $$\begin{aligned}
    g_{\rho\rho} = 1,g_{\varphi\varphi}=\rho^2,g_{zz}=1
    \end{aligned}$$
  • 于是我们还得到了弧长微分
    $$\begin{aligned}
    ds_{\rho} = d\rho,ds_{\varphi}=\rho d\varphi,dz=dz
    \end{aligned}$$
  • 于是我们还得到了面元微分
    $$\begin{aligned}
    d\sigma_{\rho\varphi}=\rho d\rho d\varphi,d\sigma_{\rho z}=d\rho dz,d\sigma_{z\varphi}= \rho dzd\varphi
    \end{aligned}$$
  • 我们还得到了体积元微分
    $$\begin{aligned}
    dV = \rho d\rho d\varphi dz
    \end{aligned}$$
• 笛卡尔坐标系与球坐标系的变换
  参见上面的栗子就可以得到相应结论，略去
• 小声
  有一说一，其实上面的推导像极了高等数学中在讲述多元函数微分时的某些玩意儿(不能说很像，其实就是一摸一样)

曲线坐标系下的向量场梯度表达式

• 定义在$R^3$空间中的标量场函数$\psi$，其梯度为不依赖于坐标的算符表达式为$\nabla \psi$，由梯度的定义可知(想想全微分表达式叭)
  $$\begin{aligned}
  \nabla \psi \cdot \mathrm{d}s = \mathrm{d}\psi \Leftrightarrow (\nabla \psi)_i \cdot \mathrm{d}s_i = \mathrm{d}\psi
  \end{aligned}$$
  • 在曲线坐标系中，$\mathrm{d}s_i = h_i\mathrm{d}u_i$，$\psi=\psi(u_1,u_2,u_3)$，$\mathrm{d}\psi = \frac{\partial \psi}{\partial u_i}\mathrm{d}u_i$
    因此在曲线坐标系中的梯度的第$i$个分量的表达式为
  • $$\begin{aligned}
    (\nabla \psi)_i = \frac{1}{h_i}\frac{\partial \psi}{\partial u_i}
    \end{aligned}$$
    于是在曲线坐标系中标量场$\psi$的梯度表达式为
  • $$\begin{aligned}
    \nabla\psi = \frac{1}{h_1}\frac{\partial \psi}{\partial u_1}\vec{e_1}+\frac{1}{h_2}\frac{\partial \psi}{\partial u_2}\vec{e_2}+\frac{1}{h_3}\frac{\partial \psi}{\partial u_3}\vec{e_3}
    \end{aligned}$$
  • 曲线坐标系下的梯度算子为*
    $$\begin{aligned}
    \nabla = \sum_{i=1}^3\frac{1}{h_i}\frac{\partial }{\partial h_i}\vec{e_i}
    \end{aligned}$$
    $\vec{e_i}$为曲线坐标系下的基向量
• 柱坐标系下的梯度算子
  $$\begin{aligned}
  \nabla = \frac{\partial}{\partial \rho}\vec{e_{\rho}}+\frac{1}{\rho}\frac{\partial }{\partial \varphi}\vec{e_{\varphi}}+\frac{\partial }{\partial z}\vec{e_z}
  \end{aligned}$$
• 球坐标系下的梯度算子
  $$\begin{aligned}
  \nabla = \frac{\partial}{\partial r}\vec{e_r}+\frac{1}{r}\frac{\partial }{\partial \theta}\vec{e_{\theta}}+\frac{1}{r\sin{\theta}}\frac{\partial }{\partial \varphi}\vec{e_{\varphi}}
  \end{aligned}$$

曲线坐标系下的向量场散度表达式

• 
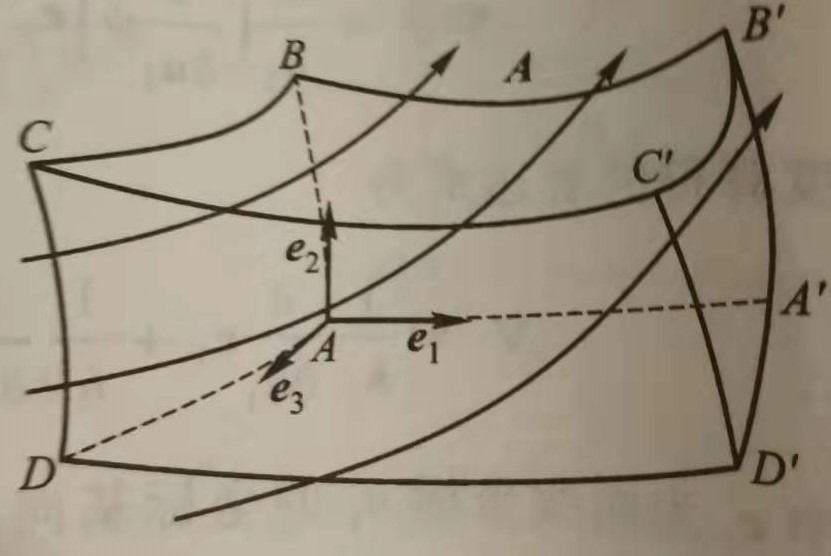
• 在空间中取一微小体积元，体积元的边是坐标曲线构成的一个曲边六面体，八个顶点如上图表示，基向量也如上图所示。$AA’=ds_1,AB=ds_2,AD=ds_3$，顶点坐标表征为$A(u_1,u_2,u_3),A’(u_1+du_1,u_2,u_3),B(u_1,u_2+du_2,u_3),D(u_1,u_2,u_3+du_3)$，其余坐标可参此写出。根据前述内容可以得到$ds_1=h_1du_1,ds_2=h_2du_2,ds_3=h_3du_3$
• 曲边六面体的六个面都是某一曲面的等值面，例如曲面$\Sigma_{ABCD}是u_1$的等值面，记为$\Sigma_{ABCD} = d\sigma_1$，其对应面$\Sigma_{A’B’C’D’} = d\sigma_1’$，其余各面参此表示。面积的表示为
  $$\begin{aligned}
  d\sigma_1 = ds_2ds_3=h_2h_3du_2du_3
  \end{aligned}$$
  其余各个式子照此表征
• 根据向量场A散度的定义
  $$\begin{aligned}
  \nabla\cdot A = \lim_{\Delta V\to 0}\frac{1}{\Delta V}\oint_{\Sigma}A\cdot d\sigma
  \end{aligned}$$
  (注意散度(包括旋度)中的元素都是向量)
  其中$\Sigma$为小体积$\Delta V$的边界，而$\Sigma$上的面元$d\sigma$的正向规定为外法向。向量场A在基向量$e_1,e_2,e_3$的分量分别为$A_1,A_2,A_3$，由此可将上式用各个分量表征。
  由于规定外法向为正向，因此流入平面的通量为负，流出平面的通量为正，于是$d\sigma_1 $上的通量为
  $$\begin{aligned}
  -A_1(u_1,u_2,u_3)h_2(u_1,u_2,u_3)h_3(u_1,u_2,u_3)du_2du_3
  \end{aligned}$$
  $d\sigma_1’ $上的通量为
  $$\begin{aligned}
  A_1(u_1+du_1,u_2,u_3)h_2(u_1+du_1,u_2,u_3)h_3(u_1+du_1,u_2,u_3)du_2du_3
  \end{aligned}$$
  将上式泰勒展开到一阶，并略去高阶小量(操作完后应该只剩三项)
  因此净通量为
  $$\begin{aligned}
  \frac{\partial (A_1h_2h_3)}{\partial u_1}du_1du_2du_3
  \end{aligned}$$
  同理可以得到另外两个对面的净通量
  注意到$\Delta V =dV =h_1h_2h_3du_1du_2du_3$
  带入散度的定义式就可以得到
  $$\begin{aligned}
  \nabla\cdot A = \frac{1}{h_1h_2h_3}[\frac{\partial (A_1h_2h_3)}{\partial u_1}+\frac{\partial (A_2h_3h_1)}{\partial u_2}+\frac{\partial (A_3h_1h_2)}{\partial u_3}]
  \end{aligned}$$
• 柱坐标系下的散度表达式
  柱坐标系的度量因子分别为$h_1 =1,h_2=\rho,h_3=1$，柱坐标系下向量场A由基向量表征为:
  • $$\begin{aligned}
    \nabla \cdot A = \frac{1}{\rho}[\frac{\partial (\rho A_{\rho})}{\partial \rho}+\frac{\partial A_{\varphi}}{\partial \varphi}+\frac{\partial A_z}{\partial z}]
    \end{aligned}$$
• 球坐标系下的散度表达式
  球坐标系的度量因子分别为$h_1 = 1,h_2=r,h_3=r\sin\theta$向量场A在基向量下的表达式为
  • $$\begin{aligned}
    \nabla \cdot A = \frac{1}{r^2\sin\theta}[\frac{\partial (A_r r^2\sin\theta)}{\partial r}+\frac{\partial (A_{\theta}r\sin\theta)}{\partial \theta}+\frac{\partial (A_{\varphi}r)}{\partial \varphi}]
    \end{aligned}$$

曲线坐标系下的向量场旋度表达式

• 根据旋度的定义，向量场A的旋度为
  $$\begin{aligned}
  (\nabla\times \vec{A})\cdot\vec{n} = \lim_{\Delta \sigma\to 0}\frac{1}{\Delta \sigma}\oint_l\vec{A}\cdot d\vec{l}
  \end{aligned}$$
  $\vec{n}$是面元的单位法向量，方向满足右手螺旋，l为面元$\Delta\sigma$边界的闭合曲线，沿l的正向绕行时，面元区域始终在左侧。
• 为了简便起见(偷懒)，我们直接按照旋度的定义给出结论
  
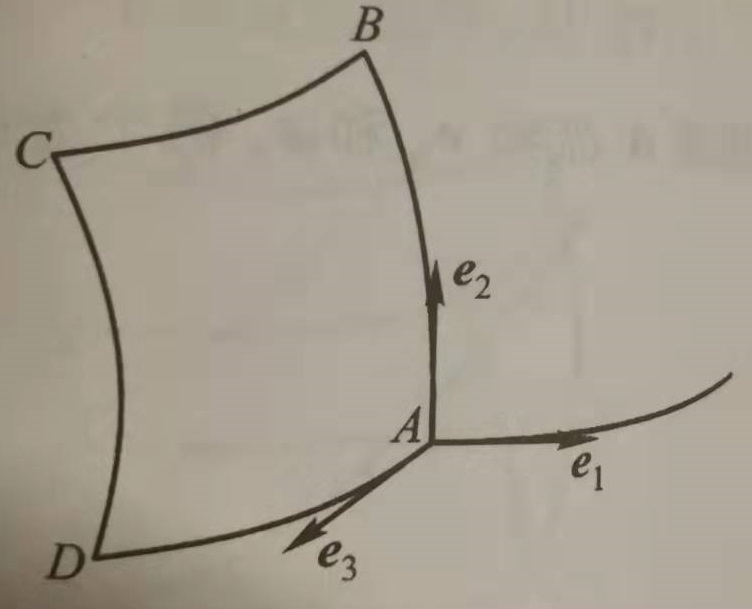
  $$\begin{aligned}A(u_1,u_2,u_3),B(u_1,u_2+du_2,u_3),C(u_1,u_2+du_2,u_3+du_3),D(u_1,u_2,u_3+du_3)\end{aligned}$$
  $$\begin{aligned}\overline{AB}=ds_2=h_2(u_1,u_2,u_3)du_2 \
  \overline{BC}=ds_3’=h_3(u_1,u_2+du_2,u_3)du_3 \
  \overline{CD}=-ds_2’=-h_2(u_1,u_2+du_2,u_3+du_3)du_2 \
  \overline{DA}=-ds_3=-h_3(u_1,u_2,u_3)du_3\end{aligned}$$
• 显然向量场A也可以按照基向量方向分解，由于都在等值面$u_1$上，这里将之略去，于是根据定义
  $$\begin{aligned}
  d\sigma = ds_2ds_3 = h_2h_3du_2du_3 \\
  (\nabla\times\vec{A})_1 = A_2(u_2,u_3)\overline{AB} \\
  +A_3(u_2+du_2,u_3)\overline{BC} \\
  +A_2(u_2+du_2,u_3+du_3)\overline{CD} \\
  +A_3(u_2,u_3)\overline{DA}
  \end{aligned}$$
  同样地，对上式一阶展开，并略去高阶小量整理得到
  $$\begin{aligned}
  (\nabla\times\vec{A})_1 = \frac{1}{h_2h_3}[\frac{\partial }{\partial u_2}(A_3h_3)-\frac{\partial }{\partial u_3}(A_2h_2)]
  \end{aligned}$$
  注意式子的轮换对称性，同理得到另外两项
  因此向量场A的旋度在曲线坐标系下的表达式为
  $$\begin{aligned}
  \nabla\times A = \frac{1}{h_2h_3}[\frac{\partial }{\partial u_2}(A_3h_3)-\frac{\partial }{\partial u_3}(A_2h_2)]\vec{e}_1 \\
  +\frac{1}{h_3h_1}[\frac{\partial }{\partial u_3}(A_1h_1)-\frac{\partial }{\partial u_1}(A_3h_3)]\vec{e}_2 \\
  +\frac{1}{h_1h_2}[\frac{\partial }{\partial u_1}(A_2h_2)-\frac{\partial }{\partial u_2}(A_1h_1)]\vec{e}_3
  \end{aligned}$$
  在笛卡尔坐标系下度量因子全为1，此时就退化为笛卡尔坐标系下的矩阵表达式
  $$rot A=\nabla\times A =\begin{pmatrix}
  i&j&k \\
  \frac{\partial }{\partial x}&\frac{\partial }{\partial y}&\frac{\partial }{\partial z} \\
  P&Q&R
  \end{pmatrix}$$

曲线坐标系下的拉普拉斯算子、表达式

• 拉普拉斯算子$\nabla^2 = \nabla\cdot\nabla$，算符作用在标量函数上可以看作梯度函数的散度，其结果仍然是梯度
  $$\begin{aligned}
  \nabla^2\psi = \frac{1}{h_1h_2h_3}[\frac{\partial }{\partial u_1}(A_1h_2h_3)+\frac{\partial }{\partial u_2}(A_2h_3h_1)+\frac{\partial}{\partial u_3} (A_3h_1h_2)]
  \end{aligned}$$
  $$\begin{aligned}
  d\psi = \nabla\psi\cdot d\vec{s} \\
  \nabla\psi_i\cdot d\vec{s}_i = \nabla\psi_i\cdot h_idu_i= d\psi_i \\
  \nabla\psi_i = \frac{1}{h_i}\frac{\partial \psi}{\partial u_i}
  \end{aligned}$$
  因此
  $$\begin{aligned}
  \nabla^2\psi = \frac{1}{h_1h_2h_3}[\frac{\partial }{\partial u_1}(\frac{h_2h_3}{h_1}\frac{\partial \psi}{\partial u_1})+\frac{\partial }{\partial u_2}(\frac{h_3h_1}{h_2}\frac{\partial \psi}{\partial u_2})+\frac{\partial}{\partial u_3} (\frac{h_1h_2}{h_3}\frac{\partial \psi}{\partial u_3})]
  \end{aligned}$$

• 拉普拉斯算子$\nabla^2 =\nabla\cdot\nabla$
  算符作用在向量函数上结果仍然是向量，我们知道一个向量可以写成基向量的线性表达式,因此对向量函数运算拉普拉斯算子等价于拉普拉斯算子作用在各个分量上，各个分量是标量函数，于是再次递归到拉普拉斯算子作用与标量函数上，因此满足

  • $$\begin{aligned}
    \vec{A}(\vec{X}) = \sum_{i=1}A_i(\vec{x})\vec{e}_i
    \end{aligned}$$
  • $$\begin{aligned}
    \nabla^2 A_i = \frac{1}{h_1h_2h_3}[\frac{\partial }{\partial u_1}(\frac{h_2h_3}{h_1}\frac{\partial A_i}{\partial u_1})+\frac{\partial }{\partial u_2}(\frac{h_3h_1}{h_2}\frac{\partial A_i}{\partial u_2})+\frac{\partial}{\partial u_3} (\frac{h_1h_2}{h_3}\frac{\partial A_i}{\partial u_3})]
    \end{aligned}$$
• • $$\begin{aligned}
    \nabla^2 \vec{A} = \sum_{i=1}(\nabla^2 A_i)\vec{e}_i
    \end{aligned}$$

• 拉普拉斯算子在物理学中具有十分重要的地位

  • 拉普拉斯方程
    $\nabla^2\psi = 0$
  • 泊松方程
    $\nabla^2\psi=\rho$
  • 运输方程
    $\frac{\partial \psi}{\partial t} -a^2\nabla ^2\psi=f$
  • 波动方程
    $\frac{\partial^2 \psi}{\partial t^2}-a^2\nabla^2\psi=f$
  • 亥姆霍兹方程
    $\nabla^2\psi+k^2\psi=0$
  • 薛定谔方程
    $i\hbar\frac{\partial \psi}{\partial t}=-\frac{\hbar^2}{2m}\nabla^2\psi+V\psi$