基本放大电路
请注意,本文最近一次更新于:2021-11-17,文章内容可能已经不具有时效性,请谨慎参考
本文最后更新于:2021年11月17日星期三晚上11点04分 +08:00
基本放大电路是电路的一种,可以应用在电路施工中。基本放大电路输入电阻很低,一般只有几欧到几十欧,但其输出电阻却很高。
基本直放大电路既可以放大交流信号,也可放大直流信号和变化非常缓慢的信号,且信号传输效率高,具有结构简单、便于集成化等优点,集成电路中多采用这种耦合方式。
2.1放大的概念和放大电路的主要性能指标
2.1.1 放大的概念
- 放大电路放大的本质是能量的控制和转换
- 电子电路放大的基本特征是功率放大
- 能够控制能量的元件称为有源元件
- 放大的前提是不失真,即只有在不失真的情况下才有意义.晶体管和场效应管是放大电路的核心元件,只有当晶体管工作在放大区、场效应管工作在恒流区时,才能使输出量和输入量始终保持线性关系,电路才不会失真.
2.1.2 放大电路的性能指标
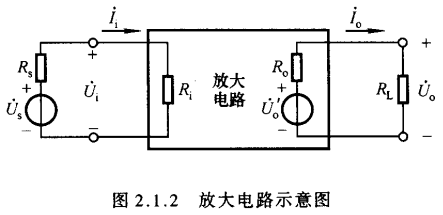
对于信号而言,任何一个放大电路均可看成一个二端口网络。左侧为输入端口,右侧为输出端口。当内阻为$R_s$的正弦波信号源$\dot{U_s}$作用时,放大电路得到的输入电压为$\dot{U_i}$,同时产生的输入电流为$\dot{I_i}$;右侧输出端口的输出电压为$\dot{U_o}$,输出电流为$\dot{I_o}$,$R_L$为负载电阻。不同的放大电路在相同的输入信号源和负载电阻下,输入电流、输出电压、输出电流将不同,这表明不同的放大电路从信号源索取的电流不同,且对同样信号的放大能力也不同.此外,同一放大电路对不同频率的信号放大能力也不同
$\color{lime}{主要参数指标}$
- $\color{yellow}{一:放大倍数}$
- 放大倍数是直接衡量放大电路放大能力的重要指标,其值为输出量$\dot{X_o}$与输入量$\dot{X_i}$之比
- 电压放大倍数是指输出电压与输入电压之比
- 电流放大倍数是指输出电流与输入电流之比
- 电压对电流放大倍数是指输出电压与输入电流之比,也称为互阻放大倍数
- 电流对电压放大倍数是指输出电流与输入电压之比,也称为互导放大倍数
- $\color{yellow}{二:输入电阻}$
- 输入电阻是从放大电路输入端看进去的等效电阻,定义为输入电压有效值$U_i$和输入电流有效值$I_i$之比,即
$$\begin{aligned}
R_i = \frac{U_i}{I_i}
\end{aligned}$$ - 输入电阻越大,信号源内阻的压降越小,信号电压损失越小,表明放大电路从信号源索取的电流越小。
- 输入电阻是从放大电路输入端看进去的等效电阻,定义为输入电压有效值$U_i$和输入电流有效值$I_i$之比,即
- $\color{yellow}{三:输出电阻}$
- 任何放大电路的输出都可以等效成一个有内阻的电压源。从放大电路输出端看进去的等效内阻称为输出电阻
- 如上图所示,设放大电路空载时的输出电压为$U_o^\prime$,有负载时的输出电压为$U_o$,根据分压关系可以导出输出电阻$R_o$为
$$\begin{aligned}
R_o = (\frac{U_o^\prime}{U_0}-1)R_L
\end{aligned}$$ - 输出电阻越小,在外部负载变化时输出电压的变化就越小,也即放大电路带负载的能力越强
- $\color{yellow}{四:通频带}$
- 通频带用于衡量放大电路对不同频率信号的放大能力。一般情况下,特定的放大电路只适用于一个频率范围内的信号。放大电路放大倍数的数值与信号频率的关系曲线,称为幅频特性曲线,下图$\dot{A}_m$为中频放大倍数
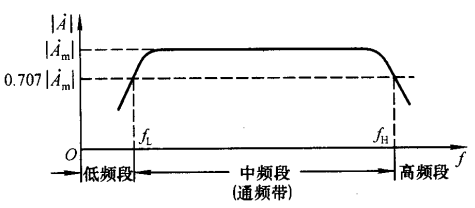
- 信号频率下降到一定程度时,使放大倍数的数值降落到$\dot{A}_m$的0.707倍的频率称为下限截止频率$f_L$
- 信号频率上升到一定程度时,使放大倍数的数值降落到$\dot{A}_m$的0.707倍的频率称为上限截止频率$f_H$
- 在两个频率阈值之间的范围称为中频段,也称为放大电路的通频带$f_{LH}$
- 通频带宽,表示放大电路对不同频率信号的适应能力强。当频率趋于零或无穷大时放大倍数的数值趋于零
- $\color{yellow}{五:非线性失真系数}$
- 由于放大器件均具有非线性特性,当输入信号幅度超过一定数值后,输出电压将会失真。输出波形中的谐波成分总量与基波成分之比称为非线性失真系数D。设基波幅值为$A_1$,谐波幅值为$A_2,A_3,\cdots$,则
$$\begin{aligned}
D = \sqrt{(\frac{A_2}{A_1})^2+(\frac{A_3}{A_1})^2+\cdots}
\end{aligned}$$
- 由于放大器件均具有非线性特性,当输入信号幅度超过一定数值后,输出电压将会失真。输出波形中的谐波成分总量与基波成分之比称为非线性失真系数D。设基波幅值为$A_1$,谐波幅值为$A_2,A_3,\cdots$,则
- $\color{yellow}{六:最大不失真输出电压}$
- 最大不失真输出电压定义为当输入电压再增大就会使输出波形产生非线性失真时的输出电压。
- $\color{yellow}{七:最大输出功率与效率}$
- 在信号不失真的情况下,负载上能够获得的最大功率称为**最大输出功率$P_{om}$**,输出电压达到最大不失真电压。
- 直流电源的能量利用率称为**效率$\eta$**,效率$\eta$定义为最大输出功率与电源消耗的功率之比
- $\color{yellow}{一:放大倍数}$
2.2基本共射放大电路的工作原理
- 下面的分析阐述以NPN型晶体管为例进行阐明
2.2.1 基本共射放大电路的工作原理
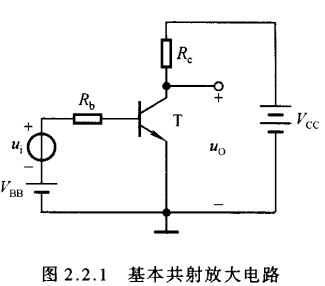
- 共射放大电路的分析
- 当$u_i$为零时,称放大电路处于静态。在输入回路中,基极电源$V_{BB}$使晶体管的基极-发射极间电压$U_{BE}$大于开启电压$U_{on}$,并与基极电阻$R_b$共同决定基极电流$I_B$;在输出回路中,集电极电源电压$V_{CC}$应当足够高,使得基极-集电极之间是反偏,以保证晶体管处于放大区的工作状态,此时$I_C = \beta I_B$。
- 当$u_i\neq 0$时,必将在静态值得基础上产生一个动态的基极电流$i_b$,在输出回路中,相应地会产生一个动态的$i_c$;集电极电阻$R_c$将集电极电流的变化反应为电压的变化,使得管压降$u_{CE}$产生变化,管压降的变化量就是输出动态电压,从而实现电压放大。
2.2.2 设置静态工作点的必要性
- $\color{yellow}{一:静态工作点}$
- 将输入信号为零,仅在直流电源单独作用时晶体管的基极电流$I_B$、集电极电流$I_C$、基极-发射极间电压$U_{BE}$、管压降$U_{CE}$称为放大电路的静态工作点Q,因此也将上述四个参量分别记为$I_{BQ},I_{CQ},I_{BEQ},I_{CEQ}$。在近似计算时常认为$U_{BEQ}$为已知量,对于硅管取值为0.6-0.8V间的某一数值,对于锗管,取值为0.1-0.3V间的某一数值。
- 静态工作点的表征
$$\begin{cases}
I_{BQ} = \frac{U_{BB}-U_{BEQ}}{R_B} \\
I_{CQ} = \bar{\beta} I_{BQ} = \beta I_{BQ} \\
U_{CEQ} = V_{CC} - I_{CQ}R
\end{cases}$$
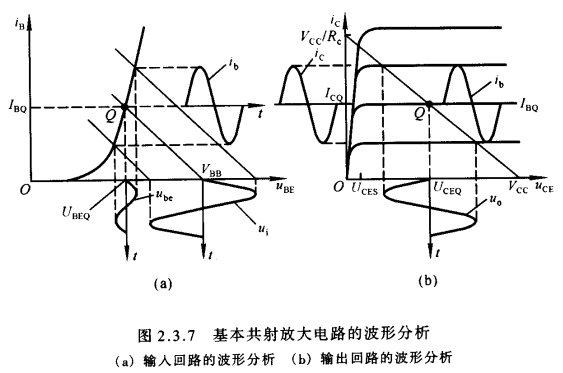
2.2.3 基本共射放大电路的工作原理及波形分析
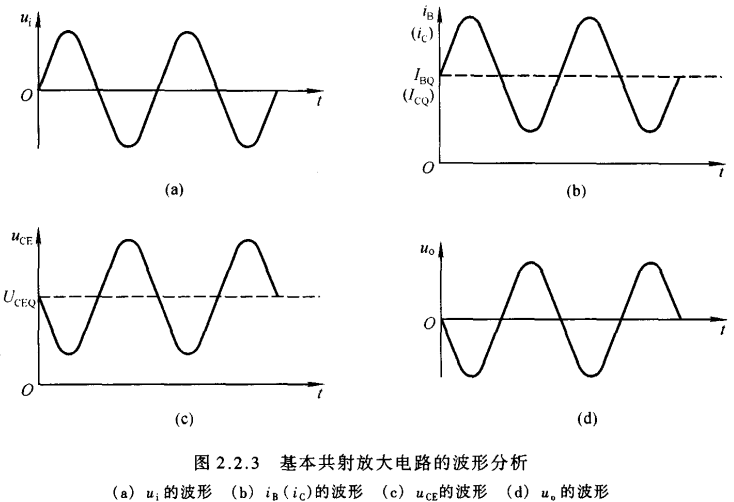
- 当有信号源电压时(有输入电压),根据前述分析,其各个电学参量将等于各个静态工作点参量叠加相应的动态参量,例如$i_B = I_{BQ} + i_b$等。因此可以得到如上波形图样。
- 以上分析可知,对于基本共射放大电路,只有设置合适的静态工作点,才能使交流分量驮载在直流分量上,以保证晶体管在输入信号的整个周期内始终工作在放大区状态,输出电压$u_o$的波形才不会产生非线性失真。
- 基本共射放大电路对电压的放大是利用晶体管对电流的放大作用,并依负载$R_c$将电流的变化反应为电压的变化
2.2.4 放大电路的组成原则
- $\color{yellow}{一:组成原则}$
略 - $\color{yellow}{二:常见的两种共射放大电路}$
- 一:直接耦合电路
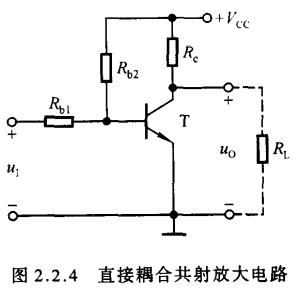
- 直接耦合电路将基极电源与集电极电源合二为一,并且放大电路与负载电阻直接相连,故称为直接耦合
- 直接耦合电路的静态工作点表征
- 将输入信号端u_i$两端短路就可以得到静态下的参量表征
- $$\begin{cases}
I_{BQ} = \frac{V_{CC} - U_{BEQ}}{R_{b2}} - \frac{U_{BEQ}}{R_{b1}} \\
I_{CQ} = \bar{\beta}I_{BQ} = \beta I_{BQ} \\
u_{CEQ} = V_{CC} - I_{CQ}R_c
\end{cases}$$ - 应当指出,该电路中的电阻$R_{b1}$是必不可少的,缺省该电阻,电路在静态下不会存在基极电流,处于截止区,电路不会正常工作。
- 二:阻容耦合电路
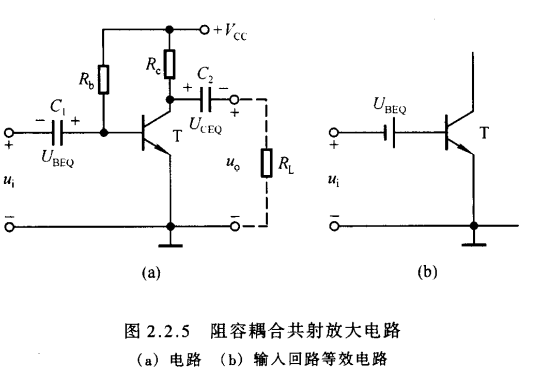
- 在电子电路中起连接作用的电容称为耦合电容,利用电容连接电路称为阻容耦合
- 根据电容的”隔直通交”性质,在信号源与放电电路、放大电路与负载之间将不存在直流分量。使电容的容值足够大,这样在输入信号的频率范围内的容抗很小,可以视为短路,输入信号几乎无损地加载在基极-发射极之间。
- 同样地,让输入端短路,就得到静态工作点表征
$$\begin{cases}
I_{BQ} = \frac{V_{CC} - U_{BEQ}}{R_b} \\
I_{CQ} = \bar{\beta}I_{BQ} = \beta I_{BQ} \\
U_{CEQ} = V_{CC} - I_{CQ}R_c
\end{cases}$$
电容$C_1$上的电压为$U_{BEQ}$,电容$C_2$上的电压为$U_{CEQ}$
- 一:直接耦合电路
2.3放大电路的分析方法
2.3.1 直流通路与交流通路
- 在放大电路中,通常直流电源与交流信号的作用总是共存的,但是由于电容、电感等电抗元件对两种信号的作用效果不尽相同,因此在实际研究过程中,我们常把直流电源和交流信号对电路的作用区分开来,形成直流通路和交流通路.
- 直流通路是在直流电源作用下直流电流流经的通路,也就是静态电流流经的通路。对于直流通路,我们做如下处理:
- 电容视为开路
- 电感线圈视为短路并且忽略电感电阻
- 信号源视为短路但保留信号源的内阻
- 交流通路是在输入信号作用下交流信号流经的通路,用于研究动态参数。对于交流通路,我们做如下处理:
- 容量大的电容如耦合电容视为断路
- 无内阻的直流电源视为短路
- 在分析放大电路时,应当遵循先静态后动态的原则,并按照前述各模型的表征式进行分析
2.3.2 围解法
- $\color{yellow}{一:静态工作点的分析}$
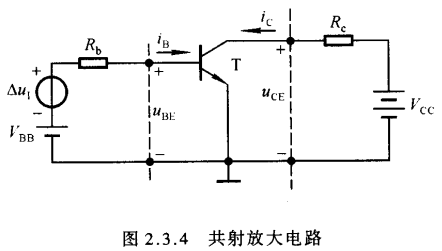
- 如前述分析所示,当信号源的输入信号为零时,此时电路为静态电路。静态工作点应该在晶体管的输入特性曲线上,并且也应当满足外部回路方程(称为输入回路负载线)
$$\begin{aligned}
U_{BE} = V_{BB} - i_{B}R_b
\end{aligned}$$
将两个图样置于同一坐标系中,两条直线的交点就是静态工作点Q(不能说十分像,但就是类比高中的欧姆定律实验中的方法,君一看便知)
同理,在输出端一侧也应满足外部回路方程(称为输出回路负载线)
$$\begin{aligned}
U_{CE} = V_{CC} - i_C R_c
\end{aligned}$$
将之与输出特性曲线置于同一坐标图场中,直线与$I_B=I_{BQ}$的交点就是静态工作点Q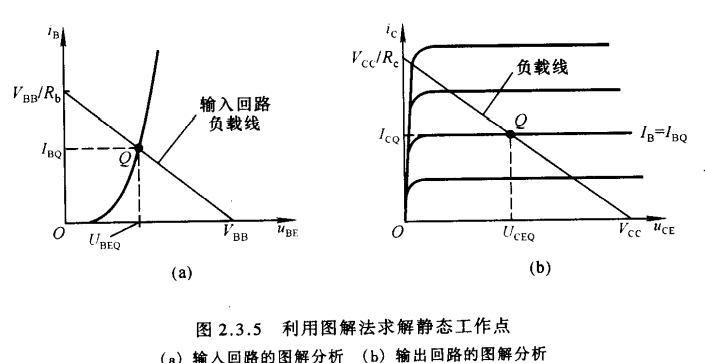
- $\color{yellow}{二:电压放大倍数的分析}$
- 当加入输入信号$\Delta u_i$时,输入回路的方程为
$$\begin{aligned}
u_{BE} = V_{BB} + \Delta u_i - i_B R_b
\end{aligned}$$ 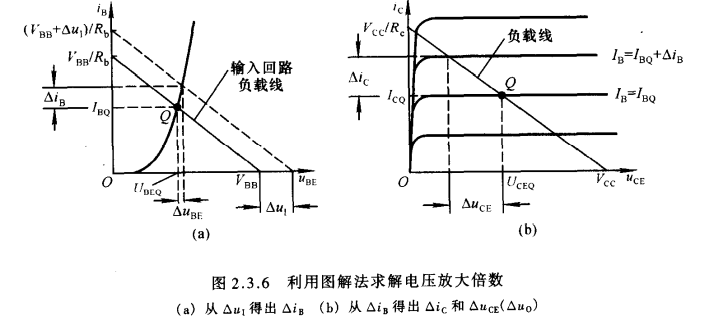
- 为求解电压放大倍数,按照以下步骤进行
- 同样地先将加有信号源的输入回路方程与输入特性曲线置于同一图场,由图场求出两直线交点的纵坐标差$\Delta i_B$
- 在输出特性曲线中,寻找$I_B = I_{BQ}+\Delta i_B$曲线与输出回路负载直线的交点,交点与标准静态工作点的横坐标差就是$\Delta u_{CE}$
- 根据电压放大倍数的定义就可得出
$$\begin{aligned}
A_u = \frac{\Delta u_{CE}}{\Delta u_i}
\end{aligned}$$
- 当加入输入信号$\Delta u_i$时,输入回路的方程为
- $\color{yellow}{三:波形非线性失真的分析}$
- 静态工作点Q的影响(默认正弦输入信号)
- 静态工作点Q合适
当静态工作点合适并且输入信号幅值较小,在放大区内集电极电流随基极电流按$\beta$倍变化,并且$i_C$与$u_{CE}$将沿负载线性变化。当$i_C$增大时,$u_{CE}$减小;当$i_C$减小时,$u_{CE}$增大。由此得到动态压降$u_{ce}$,也即输出电压$u_o$,并且$u_o$与$u_i$反向,如下图所示。
- 静态工作点Q合适
- 静态工作点Q过低
当Q点过低时,在输入信号靠近负半周峰值的某段时间内,晶体管的基极-发射极间电压小于开启电压,此时晶体管处于截止状态,因此晶体管中不会存在电流,基极电流将产生底部失真,集电极电流也会随之同步失真,而输出电压与集电极电流是反相位的,因而将产生顶部失真。因晶体管截止而产生的失真称为截止失真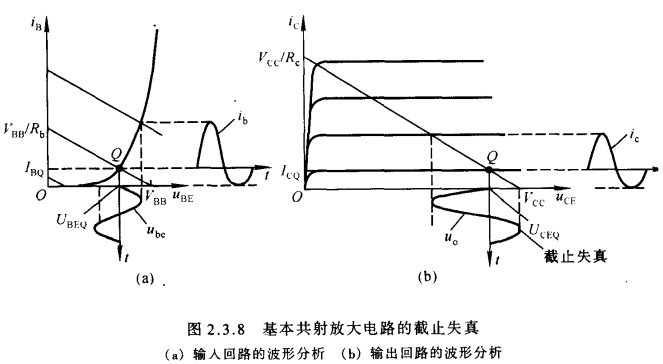
- 静态工作点Q过低
- 静态工作点Q过高
当Q点过高时,虽然基极电流不会产生失真,但是由于输入信号靠近正半周峰值的某段时间中晶体管处于饱和区,导致集电极电流产生顶部失真,而输出电压与之反相位,从而导致输出电压产生底部失真。因晶体管饱和而产生的失真称为饱和失真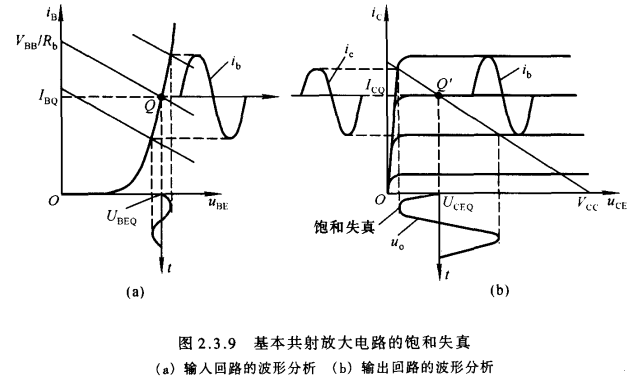
- 静态工作点Q过高
- 最大不失真输出电压
如果将晶体管的特性理想化,即认为在管压降总量$u_{CE}$最小值大于饱和管压降$U_{CES}$,即管子处于不饱和状态,且基极电流最小值大于0,即管子不截止,则非线性失真可以忽略不计.
此时以静态工作点电压$U_{CEQ}$为中心,取$V_{CC}-U_{CEQ}$和$U_{CEQ}-U_{CES}$两者中的较小值,并除以$\sqrt{2}$以得到有效值$U_{on}$,将Q设置在放大区内负载线中点处就可以得到最大的$U_{on}$
- 最大不失真输出电压
- 静态工作点Q的影响(默认正弦输入信号)
- $\color{yellow}{四:直流负载线与交流负载线}$
- 由$u_{CE}=V_{CC}-i_CR_c$所确定的负载线,称为直流负载线,动态信号遵循的负载线称为交流负载线
- 交流负载线具备两个特征
- 输入电压为$u_i$零时,晶体管的集电极电流应为静态工作点Q下的电流$I_{CQ}$,管压降应为$U_{CEQ}$,所以它必过Q点
- 由于集电极动态电流$i_c$仅决定于基极动态电流$i_b$,而动态管压降$u_{ce}$等于$i_c$与$R_c//R_L$之积,所以它的斜率为$-1/(R_c//R_L)$,因此过点Q做上述斜率的直线就是交流负载线
- 对于阻容耦合电路,只有在空载时,交流与直流负载线才重合,但对于直接耦合电路,交流与直流负载线是同一条
2.3.3 等效电路法
$\color{yellow}{一:晶体管的直流模型及静态工作点的估算法}$
- $$\begin{cases}
I_{BQ} = \frac{V_{CC}-U_{BEQ}}{R_B} \\
I_{CQ} = \bar{\beta} I_{BQ} = \beta I_{BQ} \\
U_{CEQ} = V_{CC} - I_{CQ}R
\end{cases}$$ - 将b-e间电压$U_{BEQ}$取一个固定值时,可以认为b-e间等效为一个直流恒压源,说明已将晶体管的输入特性曲线折线化.集电极电流之决定于基极电流而与静态管压降$U_{CEQ}$无关,即输出特性曲线是横轴的平行线
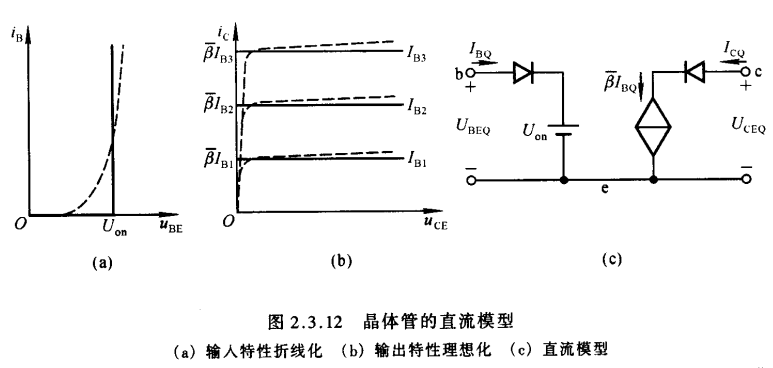
应当特别之处的是晶体管的直流模型是晶体管在静态时工作在放大状态时的模型
- $$\begin{cases}
$\color{yellow}{二:晶体管共射h参数等效模型}$
- 共射接法的放大电路在低频小信号作用下,可以将晶体管看成一个线性双口网络利用网络的h参数模型可以得出等效电路,称为共射h参数等效模型,但该模型只能用于放大电路低频动态小信号参数的分析
- h参数等效模型的由来
将晶体管的b-e端看作输入端口,c-e端看作输出端口,则h参数等效模型如下图所示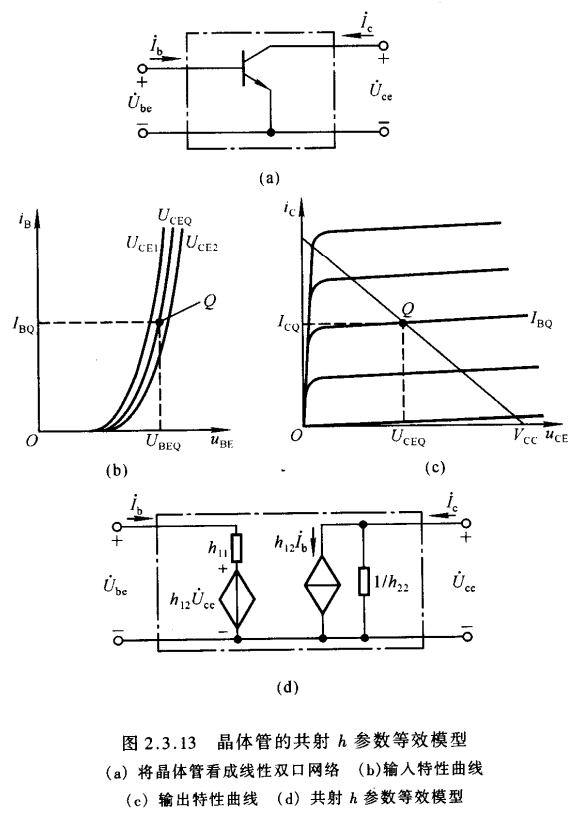
- 输入输出曲线的关系式可以写成:
- $$\begin{equation}
u_{BE} = f(i_B,u_{CE})
\end{equation}$$ - $$\begin{equation}
i_C=f(i_B,u_{CE})
\end{equation}$$
- 用$\dot{X}$表示$dX$,根据电路原理网络分析知识,可以得出h参数方程
- 方程组形式为
- $$\begin{aligned}
\dot{U}{be}=h{11}\dot{I}b+h{12}\dot{U}_{ce}
\end{aligned}$$ - $$\begin{aligned}
\dot{I}c=h{21}\dot{I}b+h{22}\dot{U}_{ce}
\end{aligned}$$
- $$\begin{aligned}
- h参数的物理意义
- $h_{11}$是当$u_{CE}=U_{CEQ}$时$u_{BE}$对$i_B$的偏导数,从输入特性曲线看就是在Q点处切线斜率的倒数.$h_{11}$表示在小信号作用下b-e间的动态电阻,常记作$r_{be}$
- $h_{12}$表示晶体管输出回路电压$u_{CE}$对输入回路电压$u_{BE}$的影响,故称为内反馈系数,内反馈系数很小
- $h_{21}$表示晶体管在Q点附近的电流放大系数
- $h_{22}$表示c-e之间的动态电导,其数值很小,也即c-e间动态电阻很大
- 简化的h参数等效模型
因为内反馈系数很小,c-e间动态电阻很大,因此在近似分析中,可以将晶体管的输入回路近似等效为只有一个动态电阻$r_{be}$看;在输出回路中,可以近似等效为一个受控电流源,简化后的等效模型如图所示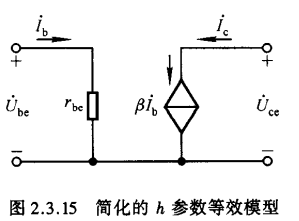
- $r_{be}$的近似表达式
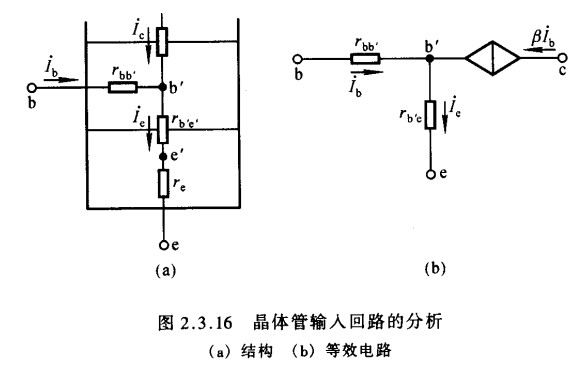
- 从上图的晶体管结构可以看出,b-e间电阻由基区体电阻$r_{bb’}$、发射结电阻$r_{b’e’}$和发射区体电阻$r_e$三部分组成,两个体电阻的阻值仅仅与杂质浓度和制造工艺有关,由于基区很薄且多子浓度很低,$r_{bb’}$数值较大,由于发射区多子浓度很大,发射区体电阻很小,相比之下可以忽略不计,因此,晶体管的输入回路等效电路如上图右侧所示,参数已标注在图上
- $$\begin{equation}
U_{be}=I_b r_{bb’}+I_e r_{b’e’}
\end{equation}$$ - $$\begin{equation}
i_E=I_S(e^{\frac{u}{U_T}}-1)
\end{equation}$$ - $$\begin{equation}
\frac{1}{r_{be’}}=\frac{\mathrm{d}i_E}{\mathrm{d}u}=\frac{I_S}{U_T}e^{\frac{u}{U_T}}
\end{equation}$$ - 小提一句,这里的$r_{be’}$就是我们之前在_post/晶体三极管.md一文中T型等效电路中提及的集电极电阻$r_e$
- 因此可以近似认为
- $$\begin{equation}
\frac{1}{r_{be’}}=\frac{1}{U_T}i_E
\end{equation}$$
- $$\begin{equation}
- 当以Q点为切点的切线取代Q点附近的曲线时,有
- $$\begin{equation}
\frac{1}{r_{be’}}=\frac{1}{U_T}i_{EQ}
\end{equation}$$
- $$\begin{equation}
- 根据定义可得
- $$\begin{aligned}
r_{be}=\frac{U_{be}}{I_b}=\frac{I_b r_{bb’}+I_e r_{b’e’}}{I_b} \\
=r_{bb’}+ (1+\beta)\frac{U_T}{I_{EQ}} \\
=r_{bb’}+ \beta\frac{U_T}{I_{EQ}}
\end{aligned}$$
- $$\begin{aligned}
$\color{yellow}{三:共射放大电路动态参数的分析}$
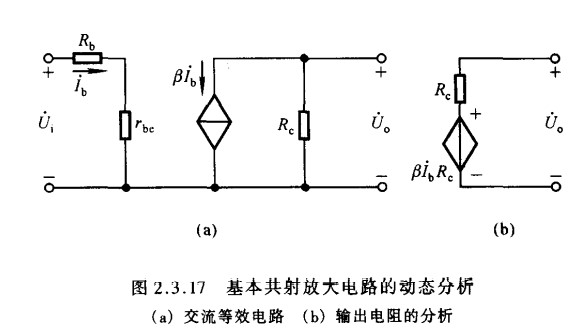
- 电压放大倍数
- $$\begin{equation}
A_u=\frac{U_o}{U_i}=-\frac{\beta R_c}{R_b+r_{be}}
\end{equation}$$
- 输入电阻
- $$\begin{equation}
R_i=\frac{U_i}{I_i}=R_b+r_{be}
\end{equation}$$
- 输出电阻
- $$\begin{equation}
R_o=R_c
\end{equation}$$
2.4放大电路静态工作点的稳定
2.4.1静态工作点稳定的必要性
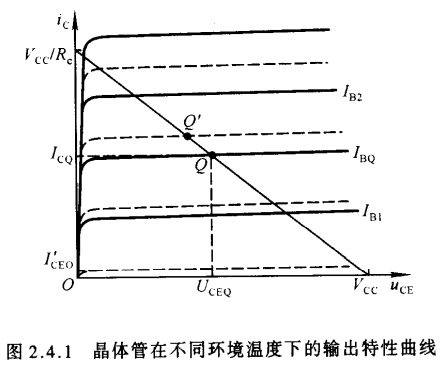
- 当环境温度上升时,共射交流放大系数$\beta$会增大,此时穿透电流$I_{CEO}$增大,在输出特性曲线中,表现为静态稳定点Q下的集电极电流$I_{CQ}$增大,静态工作点Q将沿直流负载线上升,向饱和区移动,为此,欲使得Q点回复到原来位置,需要减小基极电流$I_{BQ}$;当环境温度减小时,上述内容反之.
- 上述内容表明,在环境温度变化时,欲使静态工作点Q位置稳定不变,必须依靠调整静态稳定基极电流$I_{BQ}$来抵消$I_{CQ}$与$I_{CEQ}$的变化,因此,电路中常引入直流负反馈或温度补偿的放大使$I_{BQ}$在温度变化时与$I_{CQ}$产生相反的变化
2.4.2典型的静态工作点稳定电路
$\color{yellow}{一:电路组成和Q点稳定原理}$
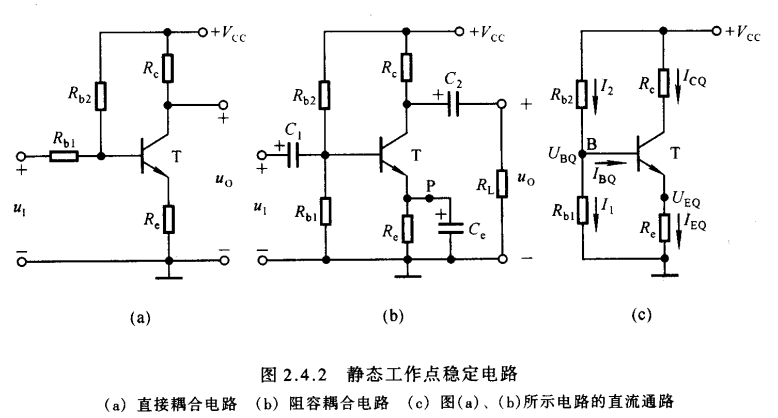
- 据上图示,(a)为直接耦合电路,(b)为阻容耦合电路,(c)为直流分析电路
- 在图(c)中,节点B的电流方程为
$$\begin{equation}
I_2=I_1+I_{BQ}
\end{equation}$$ - 为了稳定Q点,通常使参数的选取满足
$$\begin{equation}
I_1\gg I_{BQ}
\end{equation}$$ - 因此基极电位与环境温度无关
$$\begin{equation}
U_{BQ}=\frac{R_{b1}}{R_{b2}+R_{b1}}V_{CC}
\end{equation}$$
- 在图(c)中,节点B的电流方程为
- 当温度升高时,集电极电流$I_C$增大,因而发射极电流$I_E$增大,加载在发射机电阻上的电压$U_E$增大,而基极电位$U_{BQ}$不变,为此$U_{BE}$势必减小,导致基极电流减小,反馈在集电极电流上也会跟随减小,形成负反馈作用,这将使得集电极电流基本不变,从而静态工作点Q位置基本不变
- 在稳定的过程中,发射机电阻$R_e$起了重要作用,由于它的存在,产生了负反馈作用.因为此负反馈出现在直流通路中,因此$R_e$称为直流负反馈电阻
- 据上图示,(a)为直接耦合电路,(b)为阻容耦合电路,(c)为直流分析电路
$\color{yellow}{二:静态工作点的估算}$
$$\begin{equation}
U_{BQ}=\frac{R_{b1}}{R_{b1}+R_{b2}}V_{CC}
\end{equation}$$
$$\begin{equation}
I_{EQ}=\frac{U_{BQ}-U_{BE}}{R_e}
\end{equation}$$
$$\begin{equation}
U_{CEQ}=V_{CC}-I_{CQ}(R_c+R_e)
\end{equation}$$
$$\begin{equation}
I_{EQ}=(1+\beta)I_{BQ}
\end{equation}$$$\color{yellow}{三:动态参数的估算}$
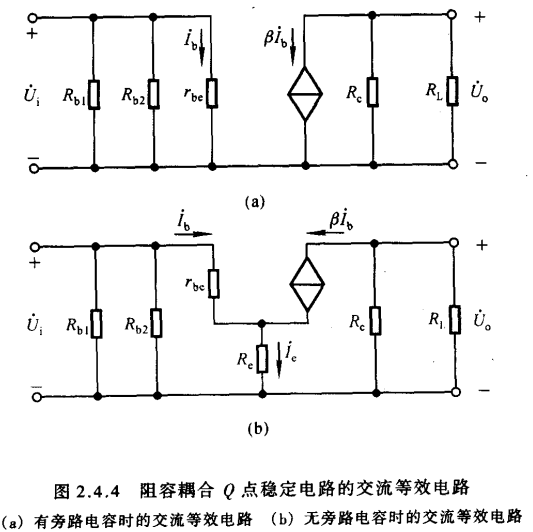
将(b)阻容耦合电路进行动态交流分析得到上图(a)中的等效电路,因此可以得到如下动态参数
$$\begin{equation}
A_v=\frac{U_o}{U_i}=\frac{\beta R_L’}{r_{be}} \quad R_L’=R_c||R_L
\end{equation}$$$$\begin{equation}
R_i=r_{be}=r_b+(1+\beta)r_e \quad r_e=\frac{V_T}{I_E}
\end{equation}$$$$\begin{equation}
R_o=r_{ce}=\frac{V_A}{I_C}
\end{equation}$$$$\begin{equation}
R_{in}=\frac{U_i}{I_i}=R_{b1}||R_{b2}||r_{be}
\end{equation}$$$$\begin{equation}
R_{out}=R_c||r_{ce}
\end{equation}$$这里需要指出的是$R_i$,$R_o$是指从晶体管的视入等效电阻,$R_{in}$,$R_{out}$是指从输入输出端视入的等效电阻,此外,晶体管的等效结构在前面已经指出过,这里遂直接使用$r_b$,$r_e$而不加详述
当原电路图中$R_e$两端不再并联旁路电容$C_e$,等效电路图如(b)所示,此时动态参数变更为
$$\begin{equation}
A_v=\frac{U_o}{U_i}=-\frac{\beta R’L}{r{be}+(1+\beta)R_e}
\end{equation}$$$$\begin{equation}
R_i=R_{b1}||R_{b2}||(r_{be}+(1+\beta R_e))
\end{equation}$$$$\begin{equation}
R_o=R_c
\end{equation}$$
当$(1+\beta)R_e\gg r_{be}$
$$\begin{equation}
A_v=-\frac{R’_L}{R_e}
\end{equation}$$
电压放大倍数仅仅取决于电阻而与环境温度无关,温度稳定性更好
2.4.3稳定静态工作点的措施
- 略
2.5晶体管放大电路的三种基本接法
2.5.1基本共集放大电路
$\color{yellow}{一:电路的组成}$
根据放大电路的组成原则,晶体管应工作在放大区,即$u_{BE}>U_{on}$且$U_{CE}\ge U_{BE}$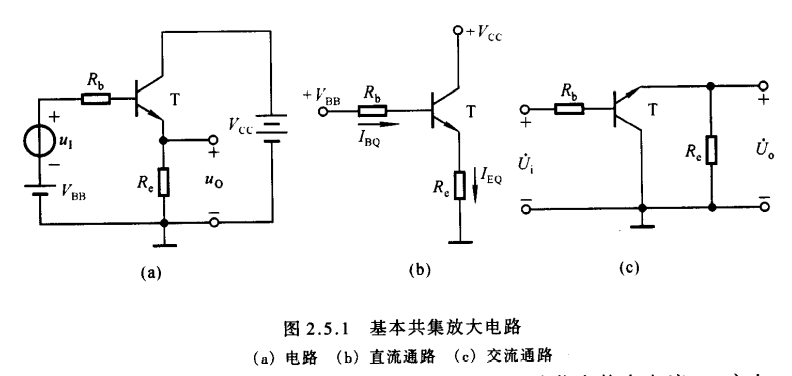
$\color{yellow}{二:静态分析}$
根据前面的内容类似分析即可
$$\begin{equation}
I_{BQ}=\frac{V_{BB}-U_{BEQ}}{R_b+(1+\beta)R_e}
\end{equation}$$$$\begin{equation}
I_{EQ}=(1+\beta)I_{BQ}
\end{equation}$$$$\begin{equation}
U_{CEQ}=V_{CC}-I_{EQ}R_e
\end{equation}$$$\color{yellow}{三:动态分析}$
画出动态通路进行分析即可,只需注意在计算输出电阻时同样地去掉输入端电压源但保留内阻,利用外加电压求解即可
$$\begin{equation}
A_v=\frac{(1+\beta) R_e}{(1+\beta) R_e+(R_b+r_{be})}
\end{equation}$$$$\begin{equation}
R_i=R_b+r_{be}+(1+\beta)R_e
\end{equation}$$$$\begin{equation}
R_o=\frac{1}{\frac{1}{R_e}+(1+\beta)\frac{1}{R_b+r_{be}}}
\end{equation}$$
这里也可以使用米勒定理快速变换,奖输入端的阻抗等效到输出端上,便可以快速写出答案
$$\begin{equation}
R_o=R_e||\frac{R_b+r_{be}}{1+\beta}
\end{equation}$$
2.5.2基本共基放大电路
$\color{yellow}{一:电路的组成}$
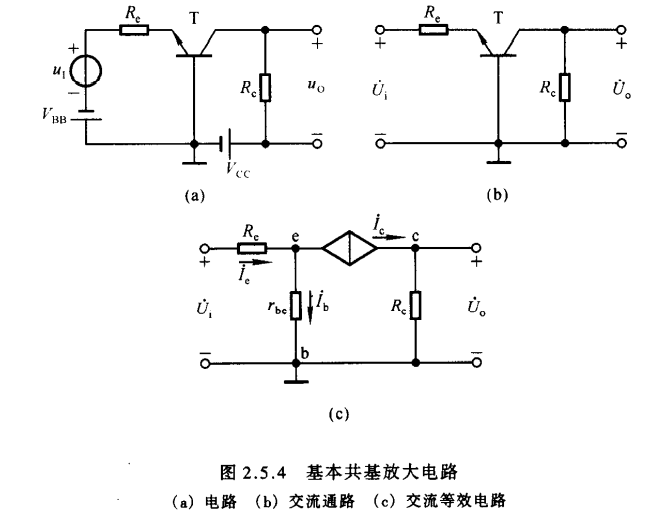
$\color{yellow}{二:静态分析}$
$$\begin{equation}
I_{EQ}=\frac{V_{BB}-V_{BEQ}}{R_e}
\end{equation}$$$$\begin{equation}
I_{BQ}=\frac{I_{EQ}}{1+\beta}
\end{equation}$$
$$\begin{equation}
U_{CEQ}=U_{CQ}-U_{EQ}=V_{CC}-I_{CQ}R_c+U_{BEQ}
\end{equation}$$
$\color{yellow}{三:动态分析}$
$$\begin{equation}
A_v=\frac{\beta R_c}{r_{be}+(1+\beta)R_e}
\end{equation}$$$$\begin{equation}
R_i=R_e+\frac{r_{be}}{1+\beta}
\end{equation}$$$$\begin{equation}
R_o=R_c
\end{equation}$$
2.5.3三种解法的比较
- 共射电路既能放大电流又能放大电压,输入电阻居三种电路之中,输出电阻较大,频带较窄,常用做低频电压放大电路
- 共集电路只能放大电流不能放大电压,是三种解法中输入电阻最大、输出电阻最小的电路,并且具有电压跟随的特点,常用于电压放大电路的输入级和输出级,在功率放大电路中常采用射极输出的形式
- 共基电路只能放大电压不能放大电流,输入电阻小,电压放大倍数、输出电阻与共射电路相当,是三种接法中高频特性最好的电路,常作为宽频带放大电路

This is an identification card as an honored membership of FeynmanDirac
Happy to see you follow FeynmanDirac, enjoy science together
 验证码启动中...
验证码启动中...
备用人机验证