Basic laws of thermodynamics
请注意,本文最近一次更新于:2022-03-12,文章内容可能已经不具有时效性,请谨慎参考
本文最后更新于:2022年3月12日星期六晚上6点18分 +08:00
本文作为热力学的开篇,将简要介绍热力学的重要基本概念
1.1热力学系统的平衡状态及其描述
- 概念
- 系统分类
- 与其他物体既==没有物质交换也没有能量交换==的系统称为==孤立系==
- 与外界==没有物质交换但存在能量交换==的系统称为==闭系==
- 与外界==既存在物质交换也存在能量交换==的系统称为==开统==
- 几点说明
- 系统由其初始状态达到平衡状态所经历的时间称为==弛豫时间==
- 系统在达到平衡状态时,系统的宏观物理量仍然会发生或大或小的==涨落==,但在热力学中我们不考虑这种涨落的存在
- 热力学中需要用到==几何、力学、电磁、化学等四类参量==来描述系统平衡状态
- 如果一个系统各部分的性质完全一致,该系统称为均匀系,一个均匀的部分称为一个相,因此均匀系也称为单相系.如果一个系统不是均匀的,但可以分成若干个均匀的部分,该系统称为复相系
1.2热平衡定律和温度
- 概念
- 温度
- 温度是描述物体冷热程度的物理量
- 两个物体系通过器壁接触时其状态可以完全独立改变,这样的器壁称为绝热的,反之称为透热的
- 热平衡定律
- 处在热平衡状态下的热力学系统,存在一个状态函数,对互为热平衡的系统,该函数函数值相等
- 热平衡定律又被称为==热力学第零定律==
- 理想气体温标
- 定容气体温度计:保持气体温度计中气体体积不变,以气体压强随其冷热程度的改变作为标志来规定其温度,并规定纯水的三相点温度为273.16K
- 以$p_t$表示三相点下气体的压强,当温度计中气体的压强为p时,规定这时气体的温度$Tv$的数值是:
$$ \begin{aligned} Tv = \frac{p}{Pt}*273.16\end{aligned} \tag{1.2.8}$$
当压强$Pt$趋向0时,公式所确定的温度趋于同一个极限温标,这个极限温标就是理想气体温标
1.3物态方程
- 概念
- 简单系统的物态方程
$$ \begin{aligned}f(P,V,T)=0\end{aligned} \tag{1.3.1}$$ - 体胀系数α
$$ \begin{aligned} α=\frac{1}{V}(\frac{\partial V}{\partial T})_p\end{aligned} \tag{1.3.2}$$ - 压胀系数β
$$ \begin{aligned} β=\frac{1}{P}(\frac{\partial P}{\partial T})_v\end{aligned} \tag{1.3.3}$$ - 等温压缩系数$\kappa_T$
$$ \begin{aligned} \kappa_T=-\frac{1}{V}(\frac{\partial V}{\partial P})_T\end{aligned} \tag{1.3.4}$$ - 热力学偏导关系
由于P、V、T满足物态方程$(1.3.1)$,其偏导数之间将存在下述关系:
$$ \begin{aligned} (\frac{\partial V}{\partial T}_P)(\frac{\partial P}{\partial T}_V)(\frac{\partial T}{\partial V}_P) = -1\end{aligned}\tag{1.3.5}$$
因此α、β、$\kappa_T$满足:
$$ \begin{aligned}α=\kappa_TβP \end{aligned} \tag{1.3.6}$$
实际中压胀系数β难以测量,一般通过$(1.3.6)$的关系确定 - 波意耳定律
对于固定质量的气体,在温度不变时其压强P和体积V的乘积是一个常数:
$$ \begin{aligned} PV=C \end{aligned} \tag{1.3.7} $$
常数C在不同的温度有不同的数值.式$(1.3.7)$称为波意耳定律 - 阿伏伽德罗定律
在相同的温度和压强下,相等体积所含各种气体的质量与他们各自的分子的分子量成正比 - 理想气体状态方程
根据波意耳定律、阿氏定律、理想气体温标的定义可以导出理想气体状态方程:
$$ \begin{aligned} PV=nRT \end{aligned} \tag{1.3.11} $$
从热力学的角度,通常认为波意耳定律、阿氏定律、焦耳定律是三个独立的实验定律.他们反映各种气体在压强趋于零时的功夫痛的极限性质.我们把严格遵从上述定律的气体称为理想气体 - 范德瓦尔斯方程
人们提出许多描述实际气体的物态方程,范德瓦尔斯方程是最常见的方程之一.对于n mol的气体,范氏方程为:
$$ \begin{aligned} (P+\frac{an^2}{V^2})(V-nb)=nRT \end{aligned} \tag{1.3.12} $$
其中a、b是常量,其值视不同的气体而异,可由实验确定
范氏方程是在理想气体物态方程的基础上考虑分子间相互作用修正而成.$(1.3.12)$中的nb是考虑分子间的斥力引进的修正项,$\frac{an^2}{V^2}$是在考虑分子之间的吸引力而引进的修正项. - 位力状态方程
昂内斯将物态方程级数展开得到:
$$ \begin{aligned} P=(\frac{nRT}{V})(1+\frac{n}{V}B(T)+(\frac{n}{V})^2C(T)+…) \end{aligned} \tag{1.3.13} $$
上式称为位力展开.其中B(T)、C(T)、……分别称为第二位力系数、第三位力系数……他们都是温度的函数 - 补充说明
经验指出,均匀热力学系统可以分为两类:一类与系统的质量或物质的量成正比,称为广延量;一类与质量或物质的量无关,称为强度量.
- 简单系统的物态方程
1.4功
- 概念
- 准静态过程
当气体的外界条件发生改变时,它的状态就会发生变化.气体从一个状态不断地变化到另一状态,所经历的是一个状态变化的过程.过程进展的速度可以很快,也可以很慢,实际过程通常比较复杂.如果过程进展得十分缓慢,使所经历的一系列中间状态都无限接近平衡状态,==(也即经历改变的时间远大于弛豫时间)==,这个过程就叫做准静态过程.==准静态过程就是实际过程无限缓慢进行的极限==.
准静态过程有一个重要的性质:如果没有摩擦力,外界在准静态过程中对系统的作用力,可以用描写系统平衡状态的参量表示出来. - 准静态过程的功
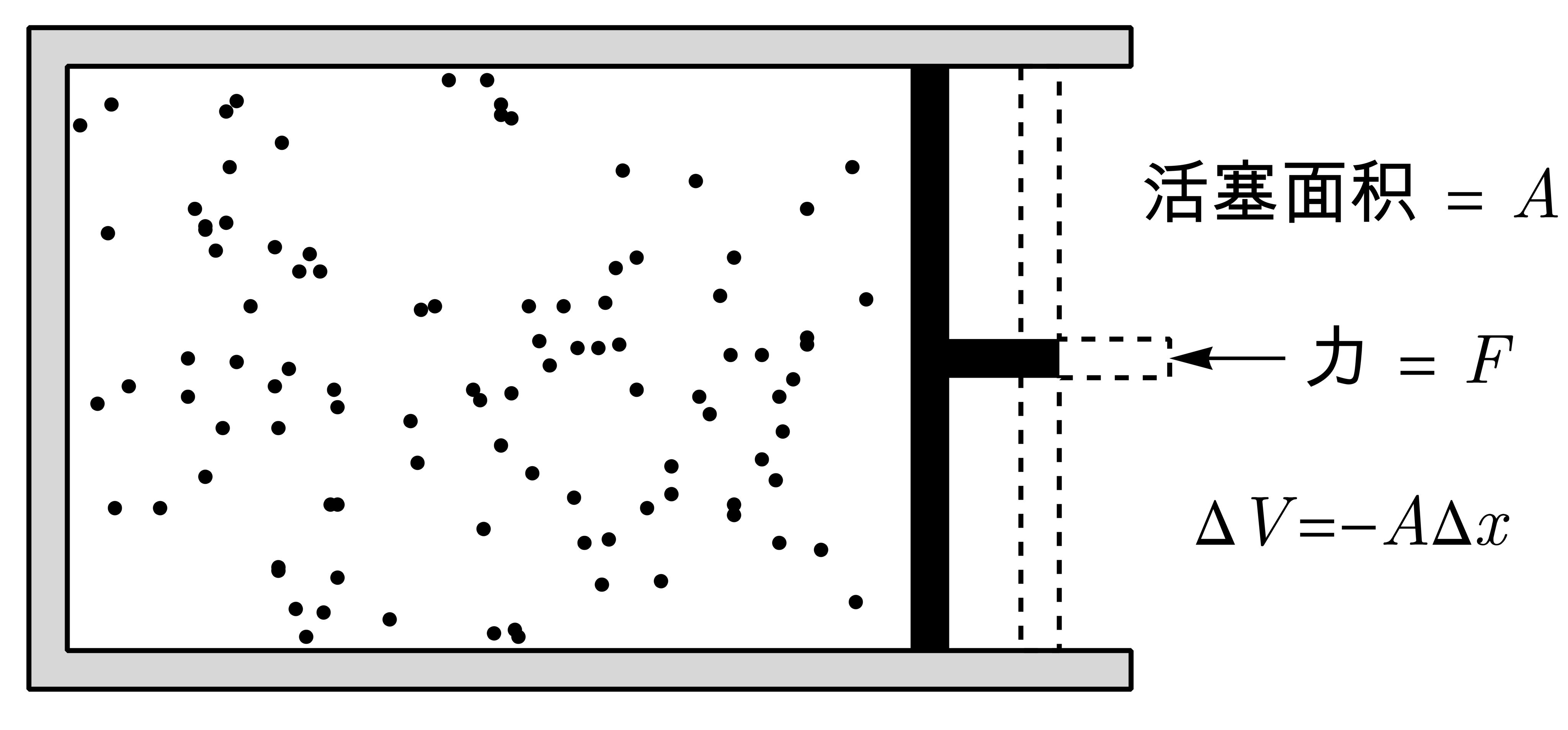
当活塞在准静态过程中移动一个距离dx时,外界对流体做的功是dW = pAdx,流体体积的变化为$\mathrm{d}$V = -Adx,故外界对系统所做的功可以表示为:
$$ \begin{aligned} \mathrm{d}W = -p\mathrm{d}V \end{aligned} \tag{1.4.1} $$
如果系统在准静态过程中的体积发生了有限的变化,例如由$V_A$变为$V_B$,则外界对系统所做的功等于:
$$ \begin{aligned} W = -\int_{V_A}^{V_B}p\mathrm{d}V \end{aligned} \tag{1.4.2} $$ - 准静态过程中几种介质的功
- 液体表面薄膜:
设有液体表面薄膜张在线框上,线框一边可以移动,以$\sigma$表示单位长度的表面张力,表面张力使液面有收缩的趋势,使可移动的边移动一个距离$\mathrm{d}$x时,外界克服表面张力做功为:
$$\begin{aligned} \mathrm{d}W = 2\sigma l\mathrm{d}x\end{aligned} $$
注意到薄膜液面面积的变化为:$\mathrm{d}A=2l\mathrm{d}x$,
从而:
$$ \begin{aligned} \mathrm{d}W = \sigma \mathrm{d}A \end{aligned} \tag{1.4.4}$$ - 电介质:
一个电势差为U的平行板电容器中电荷量增加$\mathrm{d}q$时,外界对平行板电容器所做的功为:
$$ \begin{aligned} \mathrm{d}W = U \mathrm{d}q \end{aligned} $$
平行班电容器的电荷面密度为$\sigma$,A为平行板的面积,L表示极板间距,E表征板间场强,那么:
$$\begin{aligned} \mathrm{d}q=A\mathrm{d}\sigma,EL=U \end{aligned}$$
从而可以得到:
$$\begin{aligned} \mathrm{d}W=ELA\mathrm{d}\sigma=VE\mathrm{d}\sigma \end{aligned}$$
其中V表示电解质的体积
由Gauss定理$\nabla\cdot D = \sigma $以及D = P+$\varepsilon_0$E可以得到:
$$\begin{aligned}\mathrm{d}W=V\mathrm{d}(\frac{\varepsilon_0E^2}{2})+VE\mathrm{d}P\end{aligned} \tag{1.4.6}$$
其中$\varepsilon_0$是真空介电常数,P是电极化矢量,式$(1.4.6)$表明外界对平行板电容器所做的功由两部分构成,第一式表示对激发电场做的功,第二式表示对极化电场做的功 - 磁介质:
长度为L截面积为A的磁介质上绕有N匝线圈(忽略线圈电阻).线圈中接入电流,通过改变流入的电流以改变磁介质中的磁场时,线圈中将产生反电动势,此时,外界需要克服反电动势做功,在$\mathrm{d}$t时间内外界做的功为:
$$\begin{aligned} \mathrm{d}W = UI\mathrm{d}t\end{aligned}$$
U表示反电动势大小,I为流入电流强度.设磁介质中磁感应强度为B,由法拉第电磁感应定律:
$$\begin{aligned}U = N\frac{\mathrm{d}}{\mathrm{d}t}(AB) \end{aligned}$$
由安培环路定理$\int H \cdot \mathrm{d}l = \sum i$得到HL=NI,从而得到:
$$\begin{aligned} \mathrm{d}W = (NA\frac{\mathrm{d}B}{\mathrm{d}t})(\frac{L}{N}H)\mathrm{d}t = ALH\mathrm{d}B \end{aligned}$$
即$\mathrm{d}W = VH\mathrm{d}B$,注意到B=$\mu_0$(H+M),可以得到:
$$\begin{aligned} \mathrm{d}W = V\mathrm{d}(\frac{\mu_0H^2}{2})+\mu_0VH\mathrm{d}M \end{aligned}\tag{1.4.8}$$
上式中$\mu_0$是真空磁导率,式$(1.4.8)$表明外界克服反电动势做功可以分为两部分,第一部分是对激发磁场做功,第二部分是对极化磁场做功
- 液体表面薄膜:
- 准静态过程
1.5热力学第一定律
- 概念
- 内能
- 从微观角度看,内能是系统中分子无规则运动的能量总和的统计平均值.无规则运动的能量包括动能、分子间相互作用的势能以及分子内部运动的能量.根据问题的性质,可以包括或不包括分子在外场中的势能.
- 内能是状态函数
- 内能是广延量,根据广延的性质。系统虽然没有平衡但可以可划分为若干个平衡的小区域,则整个系统的内能是各部分内能之和,即:
$$\begin{aligned} U = \sum U_i \end{aligned} \tag{1.5.5}$$
- 热力学第一定律
- 数学表达形式:
$$\begin{aligned} U_B - U_A = W + Q \end{aligned} \tag{1.5.3} $$ - 描述形式:第一类永动机是不可能造成的
- 热力学第一定律就是能量守恒定律
1.6热容和焓
- 概念
- 热容
- 定义:一个系统在某一过程中温度升高1 K 所吸收的热量,称作系统在该过程中的热容.其表征为:
$$\begin{aligned} C = \lim_{\Delta T\to \ 0}\frac{\Delta Q}{\Delta T} \end{aligned} \tag{1.6.1}$$
在国际单位制中,热容的单位是($J\cdot K^{-1}$).热容也是一个广延量. - 我们用$C_m$表示1 mol物质的热容,称为摩尔热容.摩尔热容只与物质的固有属性有关,是一个强度量.系统的热容与摩尔热容的关系为:
$$\begin{aligned} C = nC_m \end{aligned} \tag{1.6.2} $$
式$(1.6.2)$中 n 表示系统的物质的量,单位质量的物质在某一过程中的热容称为物质在该过程的比热容,以小写c表示. - 定容热容:在等容过程中系统的体积不变,那么外界对系统不做功,由热力学第一定律可知 Q = $\Delta$U,那么:
$$\begin{aligned} C_V = (\frac{\partial U}{\partial T})_V\end{aligned}\tag{1.6.3}$$ - 定压热容:在等压过程中,外界对系统做功W = -$p\Delta V$,由热力学第一定律,Q = $\Delta U + p\Delta V$,那么:
$$\begin{aligned} C_p = (\frac{\partial U}{\partial T})_p + p(\frac{\partial V}{\partial T})_p\end{aligned}\tag{1.6.4}$$
现在引进一个状态函数H,称为焓:
$$\begin{aligned} H = U +pV \end{aligned} \tag{1.6.5}$$
式$(1.6.5)$表明在等压过程中系统从外界吸收的热量等于态函数焓的增量.
因此$(1.6.4)$又可以表示为:
$$\begin{aligned} C_p = (\frac{\partial H}{\partial T})_p \end{aligned} \tag{1.6.6}$$
1.7理想气体的内能
- 概念
- 焦耳定律
- 焦耳自由膨胀实验表明气体真空膨胀过程中对外没有热量交换,又由于系统对外不做功,基于热力学第一定律$(1.5.3)$和物态方程$(1.3.1)$以及程式$(1.3.5)$可以得到:
$$\begin{aligned} (\frac{\partial U}{\partial V})_T(\frac{\partial V}{\partial T})_U(\frac{\partial T}{\partial U})_V = -1 \end{aligned} \tag{1.7.1} $$
或:
$$\begin{aligned}(\frac{\partial U}{\partial V})_T = -(\frac{\partial U}{\partial T})_V(\frac{\partial T}{\partial V})_U \end{aligned} \tag{1.7.1}$$
式$(1.7.1)$中$(\frac{\partial T}{\partial V})_U$称为焦耳系数,它描述在内能不变的过程中温度随体积的变化率.焦耳的自由膨胀实验表明焦耳系数为0,也就是说气体的内能只是温度的函数,与体积无关,这一结论被称为焦耳定律 - ==实际上,由于水的热容比气体大得多,水温的变化不易测出.实际上,1852年焦耳和汤姆孙通过节流过程发现气体的内能不仅是温度的函数,还是体积的函数==.
- 不过,焦耳定律在气体压强趋于零的极限情况下是正确的.满足焦耳定律、阿氏定律和波义耳定律的气体称为理想气体,这一点我们在之前(# 1.3)提及过.
- 理想气体的内能
- 对于理想气体,由于分子间的平均距离足够大,分子间的相互作用能可以忽略,因此内能与体积无关,由式$(1.6.3)$两端积分得:
$$\begin{aligned} U = \int C_V\mathrm{dT} + U_0 \end{aligned} \tag{1.7.4} $$
根据式焓的定义$(1.6.5)$和理想气体状态方程$(1.3.11)$可以得到理想气体的焓为:
$$\begin{aligned} H = U + pV = U + nRT \end{aligned} \tag{1.7.5} $$
可以看出理想气体的焓也是温度的函数,由式$(1.6.6)$可得理想气体焓的积分表达式为:
$$\begin{aligned} H = \int C_p\mathrm{dT} + H_0 \end{aligned} \tag{1.7.7} $$
由:
$$\begin{aligned} C_V = \frac{\mathrm{dU}}{\mathrm{dT}} \quad C_p = \frac{\mathrm{dH}}{dT} \quad H = U + nRT \end{aligned} $$
可以得到:
$$\begin{aligned} C_p -C_V = nR \end{aligned} \tag{1.7.8}$$
式$(1.7.8)$给出定压热容和定容热容之差,引入$\gamma$表征定压热容和定容热容的比值:
$$\begin{aligned} \gamma = \frac{C_p}{C_V} \end{aligned} \tag{1.7.9} $$
从而可以得到:
$$\begin{aligned} C_V = \frac{nR}{\gamma - 1} \quad C_p = \gamma\frac{nR}{\gamma - 1}\end{aligned} \tag{1.7.10}$$
1.8理想气体的绝热过程
- 概念
- 准静态绝热过程
- 由热力学第一定律U = W + Q以及绝热过程中不存在热交换,可以得到外界对气体做的功等于气体内能的增量.
准静态过程中,外界对气体做的功$\mathrm{dW} = -p\mathrm{dV}$.
由焦耳定律知内能的全微分表达式$\mathrm{dU} = C_V\mathrm{dT}$
带入得到:
$$\begin{aligned} C_V\mathrm{dT} + p\mathrm{dV} = 0 \end{aligned} \tag{1.8.1}$$
全微分理想气体状态方程得到:
$$\begin{aligned} p\mathrm{dV} + V\mathrm{dp} =nR\mathrm{dT} \end{aligned} $$
注意到$C_p - C_V = nR \quad \frac{C_p}{C_V} = \gamma$
即:$p\mathrm{dV} + V\mathrm{dp} =(\gamma - 1)C_V\mathrm{dT} = (1 - \gamma)p\mathrm{dV} $
即:$\gamma p\mathrm{dV} + V\mathrm{dp} = 0$
或:
$$\begin{aligned} \frac{\mathrm{dp}}{p}+\gamma\frac{\mathrm{dV}}{V} = 0 \end{aligned} \tag{1.8.3} $$
式$(1.8.3)$即为理想气体准静态绝热过程中的微分方程
对式$(1.8.3)$两端积分得到:
$$\begin{aligned} pV^\gamma = const \end{aligned} \tag{1.8.4}$$
由此,理想气体在绝热过程中的p-V图像相比于等温过程的斜率更大
将式$(1.8.4)$与理想气体状态方程$(1.3.11)$结合可以得到:
$$\begin{aligned} TV^{\gamma-1} = const \end{aligned}\tag{1.8.5} $$
$$\begin{aligned} \frac{p^{\gamma -1}}{T^\gamma} = const \end{aligned}\tag{1.8.6} $$ - 某一气体的$\gamma$值可以通过测量该气体中的声速确定.声速的牛顿公式是:
$$\begin{aligned} a = \sqrt{\frac{\mathrm{dp}}{\mathrm{d\rho}}} \end{aligned}\tag{1.8.7} $$ - 结合机械波一章中可以发现,这些波速的表达式具有相同的结构,即波速 = 模量➗密度的算术平方根*
其中p是压强,$\rho$是气体的密度.声波在气体中传播时,气体以声波的频率做周期性的压缩和膨胀,压强也相应改变,但考虑到压缩和膨胀过程中的振幅很小并且变化迅速,加之气体的导热系数也很小,热量来不及传递,因此可以将该过程近似地视为绝热膨胀过程.这样,式$(1.8.7)$中的全导数就应修正为偏导数,因此得到:
$$\begin{aligned} a^2 = (\frac{\partial p}{\partial \rho})_S = v^2(\frac{\partial p}{\partial v})_S \end{aligned}\tag{1.8.8}$$
式$(1.8.8)$中v=$\frac{1}{\rho}$是介质的比体积(单位质量的体积)
由理想气体绝热膨胀微分方程$(1.8.3)$得到:
$$\begin{aligned} (\frac{\partial p}{\partial v})_S = -\gamma\frac{p}{v} \end{aligned}$$
可以得到:
$$\begin{aligned} a^2 = -\gamma\frac{p}{\rho} \end{aligned} \tag{1.8.9}$$
1.9理想气体的卡诺循环
- 概念
- 卡诺循环
- 卡诺循环由两个等温过程和两个绝热过程组成.
- 在等温过程中,满足pV = nRT,由热力学第一定理可以得到:
$$\Delta U=0,W = -\int_{V_A}^{V_B} p\mathrm{dV} = -\int_{V_A}^{V_B}nRT\frac{\mathrm{dV}}{V} \quad \tag{1.9.1}$$
那么:
$$\begin{aligned} Q = U - W = RTln\frac{V_B}{V_A} \end{aligned} \tag{1.9.2}$$
因此理想气体在等温膨胀过程中吸收的热量全部转为气体对外界做的功.等温压缩过程中外界对气体做的功通过气体转化为热量传递给热源. - 在绝热过程中满足理想气体绝热过程的微分方程,因此满足:$pV^\gamma$ = const.在该过程中,由于系统与外界不存在热量交换,因此Q $\equiv$ 0.由热力学第一定律可知:$\Delta U = W$.
那么:
$$\begin{aligned} W = -\int_{V_A}^{V_B}p\mathrm{dV}
\ =\int_{V_A}^{V_B} C\frac{\mathrm{dV}}{V^\gamma}
\ = \frac{C}{\gamma - 1}(\frac{1}{V_B^{\gamma - 1}} - \frac{1}{V_A^{\gamma - 1}}) \end{aligned}$$
由于绝热过程中始终满足$pV^\gamma$ = const,因此有: $p_AV_A^\gamma = p_BV_B^\gamma$
于是:
$$\begin{aligned} W = \frac{P_BV_B - P_AV_A}{\gamma -1}
\ = nR\frac{T_B - T_A}{\gamma - 1}
\ = C_V(T_B -T_A)
\end{aligned} \tag{1.9.3} $$
(注意到:$C_V = \frac{nR}{\gamma - 1}$)
式$(1.9.3)$表明理想气体绝热过程中外界对气体做的功等于末态与初态气体内能之差,这个结果与热力学第一定律吻合.因此,在绝热膨胀过程中,外界对气体做负功,实际上是气体对外做功,因此气体的内能下降,温度降低;在绝热压缩过程中恰好相反.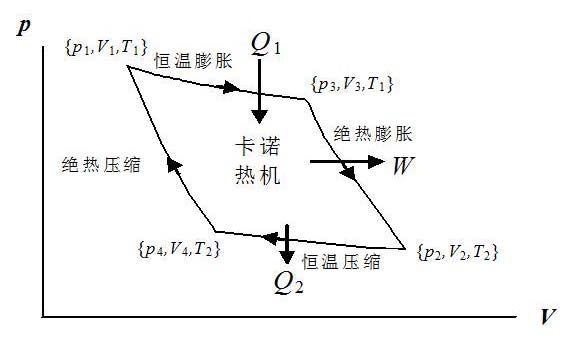
- 循环过程分析(以上图分析为例)
- 等温膨胀:
$Q_1 = nRT_1ln\frac{V_3}{V_1}$ 这里表示气体吸热 - 绝热膨胀:
$Q_2 = 0$ - 等温压缩:
$Q_3 = nRT_2ln\frac{V_2}{V_4}$ 这里表示气体放热 - 绝热压缩:
$Q_4 = 0$
整个循环完成后,理想气体回到初始状态,整个过程中内能的变化量为零,由热力学第一定律可知整个过程总外界对气体做的功等于气体在循环中吸收热量净增量的负值,也就是说气体对外做的功等于气体吸收热量的净增量,即:
$$\begin{aligned}W = Q_1 - Q_3 = nRT_1\ln(\frac{V_3}{V_1})- nRT_2\ln(\frac{V_2}{V_4})\end{aligned}$$
在两个绝热过程中满足:
$$\begin{aligned}T_1V_3^{\gamma -1} =T_2V_2^{\gamma -1}\end{aligned}$$
$$\begin{aligned}T_2V_4^{\gamma -1} = T_1V_1^{\gamma -1}\end{aligned}$$
结合上面可以得出:$$\begin{aligned} \frac{V_3}{V_1} = \frac{V_2}{V_4}\end{aligned}$$
因此:
$$\begin{aligned} W = nR\ln(\frac{V_3}{V_1})(T_1 - T_2) \end{aligned}\tag{1.9.7}$$
- 等温膨胀:
- 卡诺热机循环效率:
$$\begin{aligned} \eta = \frac{W}{Q_1} = 1 - \frac{T_2}{T_1} \end{aligned} \tag{1.9.8}$$
卡诺热机循环效率恒小于1,其比率为气体对外作用与从高温热源吸收热量的比值,热功转化效率只取决于两个热源的温度.
- 逆卡诺循环
- 我们将卡诺循环反向进行.在正向进行的卡诺循环中 W 是气体对外界做的功,反向进行后 W 就表征外界对其题做得功,其表征依然为:
$$\begin{aligned} W = nR\ln(\frac{V_3}{V_1})(T_1 - T_2) \end{aligned}\tag{1.9.7} $$
气体在低温热源吸收的热量为:
$Q_3 = nRT_2ln\frac{V_2}{V_4}$
气体在高温热源放出的热量为:
$Q_1 = nRT_1ln\frac{V_3}{V_1}$ - 你循环过程是理想制冷机的工作循环原理,其作用是将热量从低温热源转移到高温热源.可以看出,整个过程中,外界对气体做的功和气体从低温热源吸收的热量全部转移到高温热源中去,我们定义制冷机的工作效率为$\eta ‘$,那么:
$$\begin{aligned} \eta ‘ =\frac{Q_3}{W} = \frac{T_2}{T_1 - T_2} \end{aligned}$$
可见其工作效率也只取决于两个热源的温度
1.10热力学第二定律
- 概念
- 克劳修斯表述:不可能把热量从低温物体传到高温物体而不影响其他变化
- 开尔文表述:不可能从单一热源吸收热量使之完全变成有用功而不引起其他变化
- 热力学第二定律表明第二类永动机是不可能造成的
1.11卡诺定理
- 概念
- 卡诺定理
- 所有工作于两个一定温度之间的热机,以可逆机的效率最高
- 推论:所有工作于两个一定温度之间的可逆热机,他们的效率相等
1.12热力学温标(略)
- 热力学温标与理想气体温标具有一致性
1.13克劳修斯等式和不等式
- 概念
- 克劳修斯等式和不等式
- 根据卡诺定理:任何一个工作与两个温度之间的热机,可逆热机的效率最高,那么由卡诺循环效率表达式就可以得到:
$$\begin{aligned} \eta = \frac{W}{Q_1} = 1 - \frac{Q_2}{Q_1} ≤ 1 - \frac{T_2}{T_1} \end{aligned} \tag{1.13.1}$$
其中等号仅适用于可逆热机,对于不可逆热机,应该取小于号.
于是:
$$\begin{aligned} \frac{Q_1}{T_1} - \frac{Q_2}{T_2} ≤ 0\end{aligned} \tag{1.13.2}$$
式$(1.13.2)$中$Q_1 、Q_2$分别表示从高温热源$T_1$处吸收的热量和在低温热源$T_2$处放出的热量.
为方便起见,我们可以将$Q_2$定义为从低温热源处吸收的热量,于是可以得到:
$$\begin{aligned} \frac{Q_1}{T_1} + \frac{Q_2}{T_2} ≤ 0 \end{aligned}\tag{1.13.3}$$
式$(1.13.3)$称为克劳修斯等式和不等式 - 推广:
设一个系统在循环过程中与n个温度的热源接触,从这n个热源中分别吸收热量,那么:
$$\begin{aligned} \sum_{i=1}^{n} \frac{Q_i}{T_i} ≤ 0\end{aligned} \tag{1.13.4}$$
对于连续的离散点应采取积分方式
1.14熵和热力学基本方程
- 概念
- 熵
- 根据克劳修斯等式和不等式,对于可逆过程,有:
$$\begin{aligned} \oint \frac{\mathrm{dQ}}{T} = 0 \end{aligned} \tag{1.14.1}$$
对于可逆过程,积分 $\int_A^B \frac{\mathrm{dQ}}{T} $与路径无关,该态函数被定义为熵函数,熵函数是一个广延量,国际单位制中单位为J$\cdot K^{-1}$
- 热力学基本的方程
- 根据热力学第一定律:$\mathrm{dU} = \mathrm{dQ} + \mathrm{dW}$
- 根据熵的定义:$\mathrm{dS} =\frac{\mathrm{dQ}}{T}$
- 于是可以得到:
$$\begin{aligned} \mathrm{dU} = T\mathrm{dS} - p\mathrm{dV} \end{aligned} \tag{1.14.6}$$
此式为热力学的基本微分方程
1.15理想气体的熵
- 概念
- 理想气体的熵
- 根据$$ \begin{aligned} \mathrm{dU} = T\mathrm{dS} - p\mathrm{dV}
\ U = C_{V}T
\ pV = nRT
\end{aligned} $$
可以得到:
$$\begin{aligned} \mathrm{dS} = \frac{nC_V\mathrm{dT}}{T} + \frac{nR\mathrm{dV}}{V}
\end{aligned} \tag{1.15.1}$$
将pV = nRT 取对数积分得到:
$$\begin{aligned} \frac{\mathrm{dp}}{p} + \frac{\mathrm{dV}}{V} = \frac{\mathrm{dT}}{T} \end{aligned} \tag{1.15.2}$$
注意到:$C_p - C_V = nR$
可以得到:
$$\begin{aligned} \mathrm{dS} = \frac{nC_p\mathrm{dT}}{T} - \frac{nR\mathrm{dp}}{p}
\end{aligned} \tag{1.15.3}$$
1.16热力学第二定律的数学表述
- 数学推导略去
- 熵增原理结论:
==孤立系统与外界没有物质和能量交换,那么其中所发生的过程必然是绝热过程==.由此可知,孤立系统的熵永不减少,其中发生的不可逆过程总是朝着熵增的方向进行.
==系统经历可逆绝热过程后熵不变,经历不可逆绝热过程后熵增加==
1.17熵增原理的简单运用
- 略
1.18自由能和吉布斯函数
- 自由能函数
- 根据熵的定义:
$$\begin{aligned}S_B - S_A = \int\frac{\mathrm{dQ}}{T}\end{aligned}$$
在等温过程中始终满足:
$$\begin{aligned} Q\le T(S_B -S_A) \end{aligned}\tag{1.18.1}$$
其中等号在可逆过程中才成立,对于不可逆过程取小于号.
上式给出系统在等温过程中从外界吸收的热量的上限,可逆过程中取得上限.
根据热力学第一定律,$U_B - U_A = Q + W$,带入可以得到:
$$\begin{aligned} -W\le (U_A -U_B) -T(S_A -S_B) \end{aligned}\tag{1.18.2}$$
上式给出系统在等温过程中对外做功的上限,可逆过程中取得上限.
引入一个新的状态函数F,名为自由能:
$$\begin{aligned} F = U -TS \end{aligned}\tag{1.18.3}$$
$$\begin{aligned} -W\le F_A -F_B \end{aligned}\tag{1.18.4} $$
上式指出,系统在等温过程中对外做的功不大于其自由能的减小量.即==自由能的减小是等温过程中系统从外界获得的最大功==
在等容条件下W = 0,因此:
$$\begin{aligned} F_B -F_A \le 0 \end{aligned}\tag{1.18.5}$$
这就是说,在等容条件下系统的自由能永远不会增加,系统中发生的不可逆过程永远朝着自由能减少的方向进行.
- 根据熵的定义:
- 吉布斯函数
在等温等压条件下,外界对系统做的功为:W = -p($V_B - V_A$).
如果只有体积变化功,那么由$(1.18.4)$知:
$$\begin{aligned} p(V_B - V_A) \le F_A - F_B \end{aligned}\tag{1.18.6}$$
引入一个新的状态函数G,名为吉布斯函数:
$$\begin{aligned}
G = F +pV = U - TS +pV
\end{aligned}\tag{1.18.7}$$
于是可以得到:
$$\begin{aligned}
G_B - G_A \le 0
\end{aligned}\tag{1.18.8}$$
上式表明在等温等压条件下,系统的吉布斯函数永不增加;在等温等压条件下系统中发生的不可逆过程总是朝着吉布斯函数减小的方向进行的.
您阅读这篇文章共花了:

Invitation
Floral-Sunsunrise
FeynmanDirac
created:12/03/2022
Welcome to Floral-Sunsunrise
This is an identification card as an honored membership of FeynmanDirac
Happy to see you follow FeynmanDirac, enjoy science together
© 版权声明
 验证码启动中...
验证码启动中...
备用人机验证