Analog-Circuit-QAQ
请注意,本文最近一次更新于:2022-01-09,文章内容可能已经不具有时效性,请谨慎参考
本文最后更新于:2022年1月9日星期日上午10点36分 +08:00
模拟电路要点简述
常用半导体器件
- 半导体
- 1.1 纯净的具有晶体结构的半导体称为本征半导体
- 1.2 N型半导体是在本征半导体中掺入五价元素,主要靠自由电子导电
- 1.3 P型半导体是在本征半导体中掺入三价元素,主要靠空穴导电
- 1.4 多子受温度影响低,少子受温度影响高
- 1.5 向N型半导体中掺入足够的三价元素可以将其变为P型半导体
- 1.6 P型、N型半导体均呈电中性
- PN结
- 2.1 PN结具有单向导电性
- 2.2 由浓度差导致的物质粒子运动称为扩散运动,PN结结合在一起时多子会产生扩散运动
- 2.3 在PN结交界面处由于扩散运动,自由电子与空穴复合而产生空间电荷区,也称为耗尽层,形成内建电场,产生内建电动势
- 2.4 在电场作用下,少子的运动称为漂移运动,内建电场的存在是产生漂移运动的原因
- 2.5 PN结在无外场和其他激发的情况下(如热激发、光致激发),扩散运动与漂移运动平衡,PN结电流为零
- 2.6 PN结外加正向电压时(外电源正端接P,负极接N),将加剧扩散运动而抑制 漂移运动,形成正向电流,PN结导通
- 2.7 PN结反向接入时,将加剧少子漂移运动而抑制多子扩散运动,形成反向电流,近似分析中常忽略该电流
- 2.8 PN结电流方程为$i=I_{S}(e^{\frac{U}{V_{T}}}-1)$,$V_{T}=\frac{KT}{q}$是热电动势,T=300K时取26mV,$I_{S}$是反向饱和电流
- 2.9 PN结两端的反向电压达到一定程度后会被反向击穿,击穿类型分为两种:掺杂浓度高的形成齐纳击穿;掺杂浓度低的形成雪崩击穿
- 2.10 PN结具有势垒电容和扩散电容,二者之和统称为结电容
- 二极管
- 3.1 二极管具有单向导电性,并且存在正向导通开启电压$U_{on}$.对于硅型材料一般取0.7V;对于锗型材料一般取0.2V
- 3.2 近似分析时,依然用PN结电流方程及其模型处理二极管问题
- 3.3 理想二极管可以视为正向导通电压为零,反向时断路(反向截至电流为零);当存在正向导通电压时,可以视为理想二极管与一电源的串联
- 3.4 二极管的微变等效电路模型,即将二极管等效为一个动态电阻$r_{d}$,$r_{d}=\frac{V_{T}}{I_{D}}$
- 3.5 稳压二极管具有稳压特性,其正向特性与普通二极管相同,而当反向电压达到一定程度后被反向击穿后,将表现出稳压特性$U=U_{Z}$
- 晶体三极管
- 4.1 晶体三极管中由两种不同极性的电荷载流子参与导电,因而也称为双极型晶体管(BJT)、半导体三极管,简称晶体管
- 4.2 可以将晶体管视为两个PN结连结的成果,可以分为PNP型和NPN型晶体管;晶体管引出的三个电极分别为基极b、发射极e、集电极c;发射区和基区间的PN结称为发射结、集电区和基区间的PN结称为集电结
- 4.3 从符号判断晶体管类型:箭头从b->e,则为NPN型晶体管;箭头从e->b,则为PNP型晶体管
- 4.4 晶体管内部载流子运动分析(了解)
- 4.4.1 发射结加正向电压,扩散运动形成发射极电流$I_{E}$
- 4.4.2 扩散到基区的自由电子和空穴复合形成基极电流$I_{B}$
- 4.4.3 集电结加反向电压,漂移运动形成集电极电流$I_{C}$
- 4.5 晶体管的共射和共基交流放大系数
- 4.5.1 共射交流放大系数$\beta=\frac{i_{c}}{i_{b}}$
- 4.5.2 共基交流放大系数$\alpha=\frac{i_{c}}{i_{e}}$
- 4.5.3 两者的关系$\alpha=\frac{\beta}{1+\beta}$
- 4.6 晶体管的输入输出特性曲线
- 4.6.1 输入特性曲线:在管压降$U_{CE}$一定时,基极电流$i_{b}$与发射结压降$U_{be}$之间的关系
- 4.6.2 输出特性曲线:在基极电流$i_{b}$一定时,集电极电流$i_{c}$与管压降$U_{ce}$之间的关系
- 4.7 晶体管工作状态的判别(以NPN型为例)
- 4.7.1 截止区:发射结电压小于开启电压且集电结反向偏置;对于共射电路,即为$U_{be}\le U_{on}$,$U_{ce} > U_{be}$
- 4.7.2 放大区:发射结正片且集电结反偏,此时集电极电流仅仅决定于基极电流而与管压降无关,表现出$i_{b}$对$i_{c}$的控制作用,即$i_{c}=\beta i_{b}$表现在输出特性曲线上即为平行于横轴的平行线;对于共射电路,即为$U_{be}> U_{on}$,$U_{ce}\ge U_{be}$
- 4.7.3 饱和区:发射结正偏且集电结正偏,此时集电极电流与基极电流和管压降都有关;对于共射电路,即为$U_{be} > U_{on}$,$U_{ce}<U_{be}$,$i_{C}<\beta i_{b}$
- 4.7.4 临界区饱和(放大)区:$U_{ce}=U_{be}$
- 4.8 对于给定的晶体管,若集电极电位最高,则为NPN型;若集电极电位最低,则为PNP型;基极电位永远居中
- 场效应管(了解)
- 5.1 场效应管(FET)分为结型场效应管和绝缘栅型场效应管两种
- 5.2 结型场效应管又分为N沟道和P沟道两种,三个电极分别为栅极g、漏极d、源极s.在符号图中,中间为栅极g,箭头从g出发的为N沟道管,指向方向即为源极s;箭头指向g的为P沟道,出发点即为源极s
- 5.3 结型场效应管工作状态判断(N沟道管为例)
- 5.3.1 截止区(夹断区):在$U_{GS}<U_{GS(off)}$时处于夹断区,类似于发射结反偏
- 5.3.2 恒流区:$0>U_{GS}>U_{GS(off)}$,$U_{GD}<U_{GS(off)}$,类似于发射结正片集电结反偏
- 5.3.3 可变电阻区:$0>U_{GS}>U_{GS(off)}$,$U_{GD}>U_{GS(off)}$,类似于发射结、集电结正偏
- 5.3.4 可以这么类比,夹断区的条件形同与晶体管的截止区;恒流区的条件形同与晶体管的放大区;可变电阻区形同与饱和区,便于记忆
- 5.3.5 同P晶体管条件与N型晶体管相反一样,P沟道的上述条件也与N沟道相反
- 5.4 若N沟道的$U_{GS}$大于零,P沟道的$U_{GS}$小于零,则失去g-s之间等效电阻很大的特点
- 5.5 绝缘栅型场效应管
- 5.5.1 凡是在栅极-源极电压$U_{GS}$为零时电流也为零的管子就为增强型管子;凡是在$U_{GS}$为零时漏极电流不为零的就为耗尽型管子
- 5.5.2 反映在符号图上为:虚线为增强型,实线为耗尽型(虚增实耗)
- 5.5.3 耗尽型MOS管的工作状态与5.3中给出结论一致
- 5.6 增强型MOS管工作状态判断(N沟道为例)
- 5.6.1 截止区:$U_{GS}<U_{GS(th)}$,小于开启电压即截至
- 5.6.2 恒流区:$U_{GS}>U_{GS(th)}$,$U_{GD}<U_{GS(th)}$
- 5.6.3 可变电阻区:$U_{GS}>U_{GS(th)}$,$U_{GD}>U_{GS(th)}$
- 5.7 场效应管电流方程为:$i_{D}=I_{DO}(\frac{U_{GS}}{U_{GS(th)}}-1)^2$,$I_{DO}$是$U_{GS}=2U_{GS(th)}$时的电流
基本放大电路
- 因为只靠晶体管,因此以下的内容完全针对晶体管,而不涉及(或较少涉及)场效应管
- 放大电路的基本概念组
- 1.1 放大电路放大的本质是能量的控制和转换
- 1.2 放大的基本特征是功率放大
- 1.3 能够控制能量的元件称为有源元件
- 1.4 输入电阻是从放大电路输入端看进去的等效电阻,输入电阻越大,放大电路从信号源索取的电流越小,信号源内阻的压降越小,损失越小;需要强调的是输入电阻是放大电路自身的参数,与信号源电阻无关
- 1.5 输出电阻是从输出端看进去的等效内阻.任何放大电路的输出都可以等效成一个有内阻的电压源.输出电阻越小,放大电路的带负载能力越强;需要强调的是输出电阻也是放大电路自身的参数,与负载电阻无关
- 1.6 最大不失真输出电压为临界出现非线性失真时的输出电压
- 1.7 下限截止频率$f_{L}$是使得放大倍数降落到0.707倍时的频率
- 1.8 上限截止频率$f_{H}$是使得放大倍数降落到0.707倍时的频率
- 1.9 通频带是介于下限和上限截止频率之间的频率带
- 1.10 产生非线性失真的原因:由于放大器件本身具有非线性特性,因此线性放大范围有一定的限度,当输入信号幅度过高时就会产生非线性失真
- 1.11 静态工作点是输入信号为零,只存在直流电源作用时晶体管的:基极电流$I_{BQ}$、集电极电流$I_{CQ}$和发射结压降$U_{BEQ}$、管压降$U_{CEQ}$;一般我们认为$U_{BEQ}$为已知量,如前所述,对于硅取0.7V,锗取0.2V.
- 1.12 设置静态工作点的原因:保证放大电路在整个输入信号周期内始终工作在正常状态,保证电路不产生失真
- 1.13 电路要正常工作在放大状态,晶体管应处在放大区、场效应管应处在恒流区
- 1.14 直流通路是仅在直流电源作用下直流电流流经的通路
- 1.15 交流通路是仅在输入信号作用下交流信号流经的通路
- 1.16 直接耦合是放大电路与负载电阻直接相连的方式,对于直接耦合,其交直流负载线始终重合
- 1.17 阻容耦合是放大电路与负载间通过电容相连的方式,对于阻容耦合,仅在零负载下交直流负载线重合
- 非线性失真的分析
- 2.1 将一个交流小信号加载在放大电路上,在输出特性曲线上,Q点电压值$U_{CEQ}$若靠近饱和管压降$U_{CES}$则容易出现饱和失真(靠近饱和区);靠近$V_{CC}$则容易出现截止失真(靠近截止区).
- 2.2 集电极电阻电位变化与输出电压变化的相位相反的,因此集电极电阻电压与2.1变化相同,而输出电压与2.1变化相反.这就是说,若2.1中容易出现饱和失真,则集电极电流$i_{c}$容易出现顶部失真(显然集电极电流增大),而输出电压则容易出现底部失真
- 三种基本接法
- 3.1 关于如何判断是共什么电极的方法:对于一个晶体管,我们只需要判断作为信号的输入端是从什么电极进入,信号输出是从什么电极输出,则剩下的那一个电极就是用来共联的电极.简而言之,非用于承接输入输出的电极就是共联电极
- 3.2 三种接法的性质比较(建议看看)
- 3.2.1 共射接法:既能放大电流也能放大电压,具有高输出电阻、中等输入电阻和窄通频带的性质,用于一般放大
- 3.2.2 共集接法:只能放大电流不能放大电压,具有低输出电阻、高输入电阻的特性,常用做射极跟随(电压跟随)、输入级和输出级
- 3.2.3 共基电路:只能放大电压不能放大电流,具有高输出电阻、低输入电阻的特性,高频特性最好,常用于宽频带
- 三极管等效电路模型
- 略(建议自行看书)
- 复合管(两个晶体管连接)
- 5.1 复合管组成原则
- 5.1.1 保证每只晶体管都能处于放大区和有合适的通路
- 5.1.2 为了实现电流放大,应当将第一支管子的发射极或集电极与第二支管子的基极相连
- 5.2 复合管的总交流电流放大系数等于两个管子各自电流放大系数的乘积
多级放大电路
- 概念组
- 1.1 组成多级放大电路的每一个基本放大电路称为一级,级与级之间的连接称为级间耦合
- 1.2 多级放大电路的输入电阻取决于输入级所用的放大管类型和电路的基本形式;其大小就是第一级输入电阻的大小
- 1.3 多级放大电路的带负载能力的衡量,即输出电阻的大小,取决于输出级电路的基本形式,其大小就是最后一级的输出电阻大小
- 1.4 多级放大电路的低频特性取决于电路的耦合方式以及耦合电容、旁路电容的大小
- 1.5 多级放大电路的总放大能力取决于各级放大电路的放大倍数
- 直接耦合放大
- 2.1 直接耦合放大存在零点漂移现象(即温漂).温度变化引起半导体器件参数变化是产生温漂的主要原因
- 2.2 直接耦合放大具有良好的低频特性
- 2.3 抑制温漂的方法如下:在电路中引入直流负反馈,典型的就是静态工作点稳定电路中$R_{e}$的作用;采取温度补偿的方式,例如用热敏元件抵消放大管的变化;采用特性相同的管子构成差分放大电路
- 阻容耦合放大
- 3.1 阻容耦合电路中由于级间电容存在,各级静态工作点是相互独立的
- 3.2 阻容耦合低频特性差,不能放大变化缓慢的信号,因而一般只在高频、大功率情况下采用阻容耦合方式
- 3.3 由于制造大容量电容的困难,阻容耦合不便于集成化
- 差分放大电路
- 4.1 差分放大电路是构成多级直接耦合放大电路的基本单元电路
- 4.2 差分放大电路加载的共模信号是大小相等极性相同的输入信号
- 4.3 差分放大电路加载的差模信号是大小相等极性相反的输入信号
- 4.4 差分放大电路多是在电路参数理想对称的条件下进行的,参数的对称互补抑制了温漂;理想对称的差分放大电路对共模信号不放大,共模放大倍数$A_{c}=0$
- 4.5 差分放大器的四种接法具体自行看书
- 直接耦合互补输出级(OCL电路)
- 5.1 直接耦合的互补输出级是双向跟随的互补输出级,由一个NPN晶体管的射级和PNP晶体管的射级连接而成,且这两个管子参数相同,特性对称
- 5.2 由于晶体管存在开启电压$U_{be}$,因此该双向跟随互补输出电路在过零附近输出电压将产生交越失真
- 5.3 消除交越失真的方法是设置合适的静态工作点
- 直接耦合多级放大电路
- 6.1 直接耦合多级放大电路常用差分放大电路做输入级,这样可以增大共模抑制比,同时减小电路温漂
- 6.2 直接耦合放大电路的输出级常用直接耦合互补输出级电路(OCL电路),可以使输出电阻小,且带负载能力强,并且最大不失真电压幅值可以接近电源电压,进一步增强放大能力
- 6.3 直接耦合放大电路的中间级常用共射放大电路,可以得到高电压放大倍数
- 6.4 多级放大电路放大倍数的计算,建议一级一级的计算,并需要注意下级电路对上级输出电阻、上级输出电阻对下级输入电阻的影响
集成运算放大电路
- 集成运放的电路组成特点
- 1.1 集成运放一般由输入级、中间级、输出级、偏置电路构成
- 1.2 输入级一般采用差分放大电路,用于抑制温漂、增强共模抑制比、增大输入电阻和展宽频带
- 1.3 中间级一般采用共射放大电路,用于提供高电压放大倍数
- 1.4 输出级一般采用准互补输出级(OCL),用以消除交越失真和进行过流保护,并且产生小的输出电阻,增大带负载能力,增强最大不失真电压并使之接近直流电源电压
- 1.5 偏置电路一般采用多路电流源电路,用于为各级放大电路提供静态工作点、提供动态电阻和避免温漂
- 1.6 集成运算放大器适用于放大低频信号,这是因为电路中存在大量晶体管和PN结,也就存在很多结电容、分布电容
- 1.7 集成运放采用有源负载是为了增大电压放大倍数,这是因为有源负载的交流电阻理想无穷大
- 1.8 集成运放可以等效为高性能的双端输入单端输出的、具有高输入电阻低输出电阻的、能较好抑制温漂的差分放大电路
- 1.9 运算放大器的输出端是存在输出电流的
- 集成运放的重要参数列表
- 2.1 开环差模增益:在无反馈情况下,集成运放对两输入端电位差的放大能力
- 2.2 差模输入电阻:对差模电压信号源的输入电阻
- 2.3 共模抑制比:理想无穷大
- 2.4 输入失调电压:为使输出电压为零在输入端加的补偿电压
- 2.5 输入失调电流:两输入端静态电流之差的绝对值
- 电流源电路(自行看书)
- 3.1 镜像电流源
- 3.2 比例电流源
- 3.3 微电流源
- …..
- 有源负载放大电路
- 4.1 集成运放中,常用电流源电路作为有源负载替代集电极电阻$R_{c}$,这样一方面可以提供动态的电阻,一方面可以设置静态工作点
- 4.2 电路分析自行看书
放大电路的频率响应
- 概念组
- 1.1 低频特性分析:需要考虑耦合电容和旁路电容的影响,可以认为耦合电容是串入电路中,因此对高频信号相当于短路而不产生影响,而低频时会产生分压
- 1.2 高频特性分析:需要考虑极间电容和分布电容的影响,可以认为极间电容是并入电路中,因此对低频信号相当于断路而不产生影响,而高频时会产生分流
- 1.3 如前所述,共基电路的上限频率最高,因而其频带宽
- 1.4 直接耦合放大电路低频特性好,而阻容耦合电路中由于耦合电容、旁路电容多,因而低频特性差,下限频率高
- 1.5 放大电路的放大级数越多,其上限频率越低,频带越窄
- 1.6 放大电路中任何一个电容所确定的截止频率的表达式均为$f_{L}(f_{H})=\frac{1}{2\pi\tau}$,$\tau$为该电容所在回路的时间常数
- 1.7 晶体管的Π型模型
- 1.7.1 参数列表:
- $r_{bb’}$: 基区体电阻
- $r_{b’e’}$: 发射结电阻
- $r_{e}$: 发射极体电阻,常忽略不计
- $r_{b’c’}$: 集电结电阻
- $r_{c}$: 集电极体电阻,常忽略不计
- $C_{\pi}$: 发射结电容
- $C_{\mu}$: 集电结电容
- $g_{m}$: 跨导,$g_{m}=\frac{1}{r_{e}}=\frac{I_{EQ}}{V_{T}}$
- $r_{b’e}$: $r_{b’e}=(1+\beta)r_{e}=(1+\beta)\frac{V_{T}}{I_{EQ}}$
- $r_{ce}$: $r_{ce}=\frac{V_{A}}{I_{CQ}}$,常视为断路
- 1.7.2 集电结电流$I_{c}$与发射结电压$u_{b’e}$成线性关系
- 1.7.3 完整模型结构图(了解)
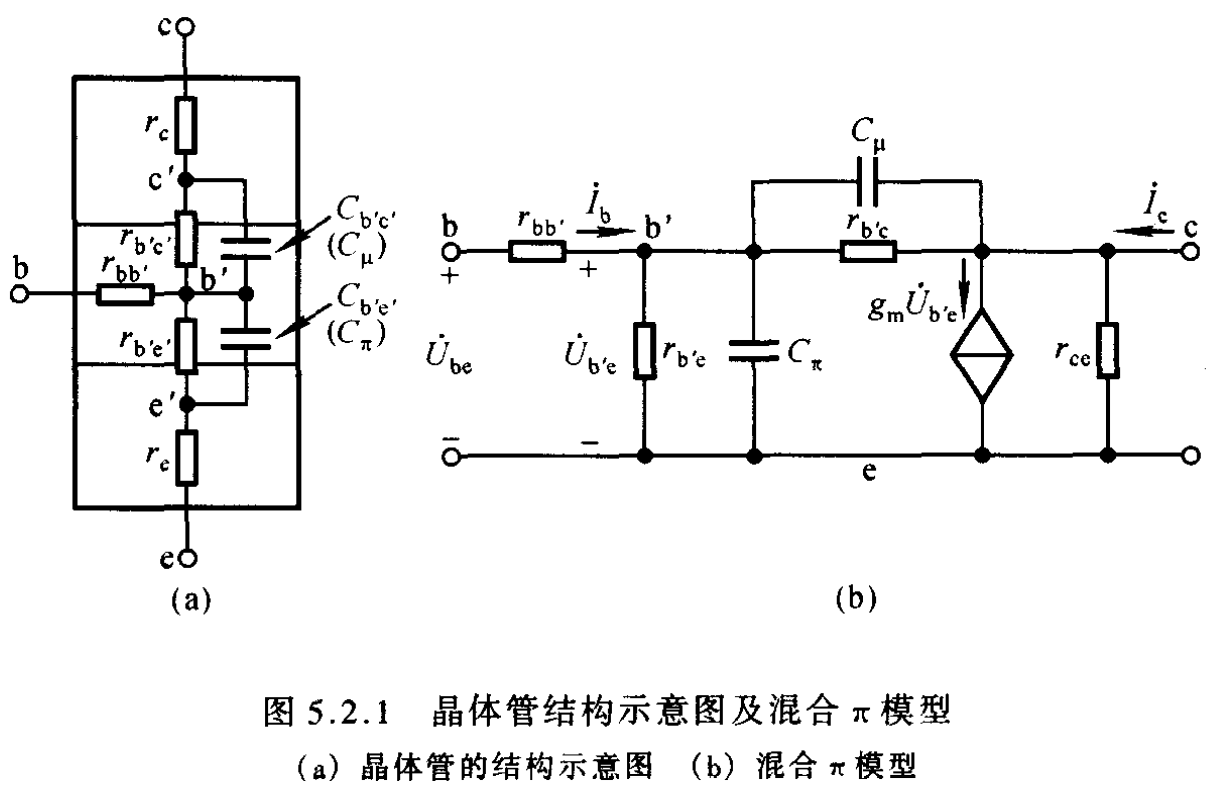
- 1.7.4 标准简化模型
- 考虑电阻$r_{b’c}$与$r_{ce}$的阻值都很大,因此视为断路而除去
- 将跨接在输入-输出回路的电容$C_{\mu}$利用米勒定理分别等效到输入输出回路之中
- $C_{\mu}’=(1-K)C_{\mu}$,$C_{\mu}’’=(1-\frac{1}{K})C_{\mu}$,$K=\frac{U_{ce}}{U_{b’e}}$
- 必备的喜闻乐见的参量$C_{\pi}’=C_{\pi}+C_{\mu}’$
- 一般地,$C_{\mu’’}$容抗远大于负载电阻,因此视为断路而忽略,便得到最终简化电路(c),这就是最终需要记住的
- 1.7.5 标准简化模型(必备)
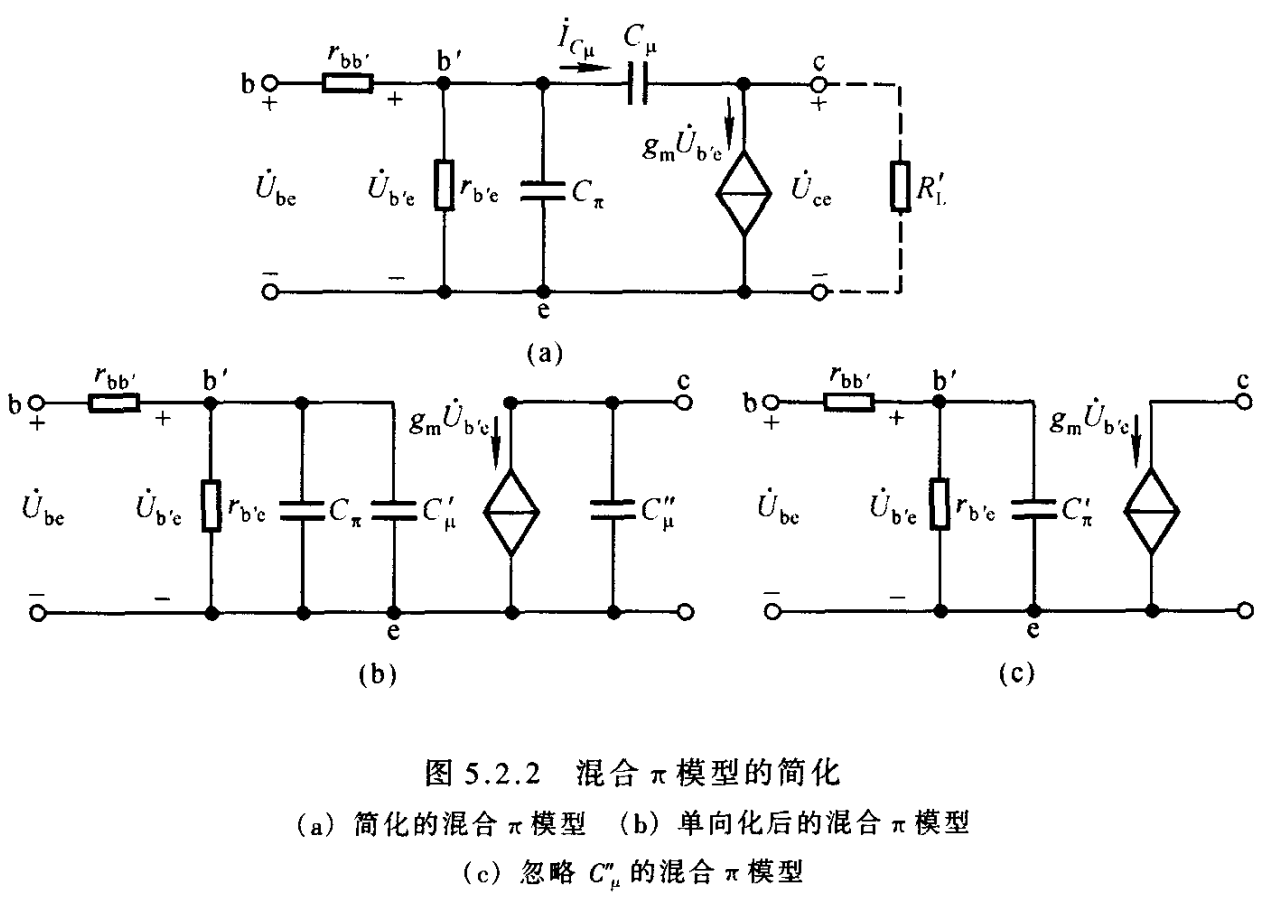
- 1.7.1 参数列表:
- 晶体管电流放大倍数的频率响应(必备)
- 2.1 共射截止频率$f_{\beta}$: $f_{\beta}=\frac{1}{2\pi r_{b’e}C_{\pi}’}$,$C_{\pi}’=C_{\pi}+C_{\mu}$
- 2.2 2.1所述的共射截止频率便是题目中常常给出的参量,一般地需要我们通过共射截止频率先行计算出$C_{\mu}$的数值大小,再按照米勒定理计算出$C_{\mu}’$并由此计算上限截止频率,因此2.1式的重要性就显而易见了
- 2.3 共基截止频率$f_{\alpha}$: $f_{\alpha}=(1+\beta)f_{\beta}$
- 2.4 2.3式是容易理解的,因为$\alpha=\frac{i_{c}}{i_{e}}=\frac{\beta}{1+\beta}\Rightarrow \frac{\alpha}{\beta}=\frac{1}{1+\beta}$,只需注意到频率需要取反便可得到,当然上面这么说只是为了理解方便
- 2.5 由2.3可以看出共基放大电路的上限截止频率远高于共射放大电路,因此共基放大电路可以作为宽频带的放大电路
- 考试中的放大电路频率响应问题
- 3.1 中频段:中频段模型就是我们最先接触到的、最熟悉的晶体管的等效模型.我们知道在该模型中是不考虑任何电容的,这是因为处于中频带时,”串接”的耦合电容(旁路电容)容抗小而视为短路;”并接”的极间电容(分布电容)容抗大而视为断路
- 3.2 低频段:如前所述,低频段时必须考虑耦合电容(旁路电容)的分压影响,极间电容(分布电容)仍然视为开路而不考虑;换言之,计算下限截止频率就要分析各个耦合电容所在回路中谁的时间常数小
- 3.3 高频段:如前所述,高频段时必须考虑极间电容(分布电容)的分流影响,耦合电容(旁路电容)视为短路而不考虑;换言之,计算上限截止频率就要分析各个极间电容所在回路中谁的时间常数大
- 3.4 求解上限、下限截止频率的关键是正确的计算回路的等效电阻
- 放大电路频率响应特性的改善和带宽的展宽
- 4.1 为降低下限截止频率,需要增大耦合电容和其等效电阻,但一般低频信号时采取直接耦合放大电路更加合适
- 4.2 提高上限截止频率,其矛盾是增益和带宽的矛盾,需要减小相应的等效电容和等效电阻阻值,还可以考虑共基放大电路
- 多级放大电路
- 5.1 对于多级放大电路,其计算建议一级一级的计算放大倍数
- 5.2 对于多级放大电路,其整个电路的下限频率一般认为是各级中最高的下限频率;上限频率一般认为是各级中最低的上限截止频率
放大电路中的反馈
- 概念组
- 1.1 反馈:存在一条通路,使得输出回路与输入回路连通,并由此影响放大电路的净输入量,则引入了反馈
- 1.2 使放大电路净输入量增大,则引入正反馈;使放大电路净输入量减小,则引入负反馈
- 1.3 反馈中存在直流量,则引入直流反馈;存在交流量,则引入交流反馈$\Leftrightarrow$仅存在于直流通路中的反馈称为直流反馈,仅存在于交流通路中的反馈称为交流反馈
- 1.4 直流反馈的主要作用是稳定静态工作点,能够克服直接耦合放大电路的零点漂移(温漂)现象
- 1.5 交流反馈的主要作用是提高放大倍数稳定性、改变输入输出电阻
- 1.6 反馈量仅仅与输出量有关,与其他任何因素,例如输入量,无关
- 1.7 串并联负反馈的判断:若输入量、反馈量、净输入量是以电压方式叠加的,则为串联反馈;若上述三量是以电流方式叠加的,则为并联反馈
- 1.8 电压电流反馈的判断:取决于反馈量的采样形式.若反馈量取自输出电压,则为电压反馈;取自输出电流,则为电流反馈$\Leftrightarrow$将输出端短路反馈量消失,则为电压反馈;将输出端断路,反馈量消失,则为电流反馈
- 1.9 正负反馈的判断:除了按照定义去看,还可以采取瞬时极性法.注意晶体管的相位反向性问题: 共射接法反相,共集、共基接法同相(即符号相同)
- 四种反馈类型的功能
- 2.1 电压串联:$U_{i}$控制$U_{o}$实现电压放大
- 2.2 电流串联:$U_{i}$控制$I_{o}$实现电压转换电流
- 2.3 电压并联:$I_{i}$控制$U_{o}$实现电流转换电压
- 2.4 电流并联:$I_{i}$控制$I_{o}$实现电流放大
- 负反馈功效
- 3.1 电压负反馈用以稳定电压、减小输出电阻
- 3.2 电流负反馈用以稳定电流,增大输出电阻
- 3.3 串联负反馈用以增大输入电阻
- 3.4 并联负反馈用以减小输入电阻
- 3.5 欲减小从信号源索取的电流并增强带负载能力就需要引入电压串联负反馈
- 3.6 欲增大从信号源索取的电流并稳定输出电流就需要引入电流并联负反馈
- 3.7 总的来说,引入负反馈可以稳定放大倍数、改变输入输出电阻、展宽频带、减小非线性失真
- 负反馈电路中的关系
- 4.0
- 4.0.1 声明:$X_{o},X_{i},X_{i}’,X_{f}$分别代表输出、输入、净输入、反馈量
- 4.0.2 我们讨论负反馈,一般是在中频带下讨论的
- 4.1 反馈系数F:$F=\frac{X_{f}}{X_{o}}$
- 4.2 开环放大倍数A:$A=\frac{X_{o}}{X_{i}’}$
- 4.3 闭环放大倍数$A_{f}$:$A_{f}=\frac{X_{o}}{X_{i}}$
- 4.4 三者关系:$A_{f}=\frac{X_{o}}{X_{i}’+X_{f}}=\frac{A}{1+AF}$
- 4.5 由4.4可见引入负反馈后电路的放大倍数缩小到原来的(1+AF)分之一
- 4.6 若发现$(1+AF)<1$,则电路引入的是正反馈;并且当$(1+AF)=0$时将产生自激振荡,产生自己振荡的条件是引入正反馈或开环状态
- 4.7 在深度负反馈条件下,即$(1+AF)\gg 1$,则$A_{f}=\frac{1}{F}$,在考试中惯用(必备)
- 4.8 需要注意深度负反馈下放大倍数仅仅决定于反馈网络,这一点固然好,但也不是反馈越深越好
- 4.9 当信号频率进入低频或高频段时,负反馈电路可能对某一特定频率产生正反馈而引起自激振荡
- 深度负反馈网络(必备)
- 5.1 深度负反馈的重要关系:$A_{f}=\frac{1}{F}$
- 5.2 深度负反馈的实质是在近似分析中忽略净输入量
- 5.3 当引入深度负反馈后就有两个重要条件(必备)
- 5.3.1 虚短:$U_{i}=U_{f}$,净输入电压忽略不计
- 5.3.2 虚断:$I_{i}=I_{f}$,净输入电流忽略不计
- 5.4 深度负反馈网络具体实例自行看书
- 理想运放(必备)
- 6.1 理想运放的特性
- 6.1.1 开环差模增益无穷大
- 6.1.2 差模输入电阻无穷大
- 6.1.3 输出电阻为零
- 6.1.4 共模抑制比无穷大
- 6.1.5 上限截止频率无穷大
- 6.2 集成运算放大器需要在线性区才能正常工作,此时需要引入负反馈
- 6.3 集成运放满足虚短路条件:$u_{P}=u_{N}$
- 6.4 集成运放满足虚断路条件:$i_{P}=i_{N}=0$
- 6.5 理想运放处于开环状态或引入正反馈时工作在非线性区
- 自激振荡(推荐)
- 7.1 在低频段,由于耦合电容、旁路电容的影响,$\dot{A}\dot{F}$将产生超前相移;在高频段,由于器件极间电容、分布电容的影响,$\dot{A}\dot{F}$将产生滞后相移.上述两种统称附加相移
- 7.2 当附加相移为$(2n+1)\pi$时就会使放大倍数增大,周而复始
- 7.3 自激振荡的产生条件是$\dot{A}\dot{F}=-1,\varphi_{A}+\varphi_{F}=(2n+1)\pi$,起振条件是$|\dot{A}\dot{F}|>1$
- 7.4 放大电路放大级数越多,引入负反馈后越容易产生高频振荡;电路中耦合旁路电容越多,引入负反馈后越容易产生低频振荡;反馈越深,满足幅值条件越容易,产生自激振荡可能性越大
- 7.5 消除自激振荡的方式可以是滞后补偿、超前补偿或RC补偿
功率输出级(必备)
- 综述
- 1.1 功率放大器一般由放大电路与大功率输出级组成
- 1.2 功率输出级是大信号输出,前述的各种模型都是小信号模型,已不再适用于分析,而只能采取图解法分析
- 分类
- 2.1 功率输出级按照静态工作点的设置可以分为甲类(A类)、乙类(B类)、甲乙类(AB类)和丙类(C类)四类
- 2.2 甲类
- 2.2.1 工作于线性区的的放大器都是甲类放大器,前述的共集、共基、共射放大电路都属于甲类
- 2.2.2 甲类电路在整个输入信号周期内都导通,导通角等于360°
- 2.2.3 甲类放大器的理论最大效率为25%
- 2.3 乙类
- 2.3.1 乙类放大器的$I_{CQ}$设置在截止点,晶体管在正半周导通而负半周截止,导通角为180°
- 2.3.2 乙类放大器的理论最大效率为$\frac{\pi}{4}$=78.5%
- 2.3.3 乙类输出级的缺点是输出波形存在交越失真,所采取的电路形态为互补推挽输出级
- 2.4 甲乙类
- 2.4.1 为了弥补乙类输出级的交越失真,甲乙类输出级采用准互补输出级OCL电路
- 2.4.2 甲乙类输出级的电路设计为互补推挽输出级提供起始偏压,从而克服交越失真
- 2.4.3 由于甲乙类输出级是OCL无电容输出级,因此其低频特性很好
各种运算电路
- 众所周知,这玩意儿最喜欢考电路设计
- 综述:考试中,分析运算电路时均认为集成运放为理想运放,满足深度负反馈条件,因而满足虚短、虚断两个条件;在分析时常运用叠加原理、节点电流法等基本电路分析方法
- 比例运算电路(必备)
- 2.1 反相比例运算电路
- 2.1.1 具体电路分析自行看书,不再展开论述
- 2.1.2 同相端接地,反相端接输入
- 2.2 同相比例运算电路
- 2.2.1 具体电路分析自行看书,不再展开论述
- 2.2.2 反相端接地,同相端接输入
- 2.2.3 虽然同相比例运算放大电路具有高输入电阻、低输出电阻的特性,但由于集成运放有共模输入,因此应当使用高共模抑制比的运放以提高运算精度
- 2.3电压跟随器
- 2.3.1 在同相比例运算电路中,将输出电压全部反馈到输入端就构成射极跟随器
- 2.3.2 此时反馈系数为1,$u_{i}=u_{P}=u_{N}=u_{o}$
- 2.4 在多级运算放大电路的分析中,只需时刻意识到各级电路的输出电阻均为零(理想运放),具有恒压特性,因此虽然后级电路是前级电路的负载,但并不影响前级电路的运算关系,因此可以完全视为独立的单极电路分析
- 2.1 反相比例运算电路
- 求和运算电路(必备)
- 3.1 求和运算电路是用以实现多个输入信号按各自不同的比例求和或求差的电路
- 3.2 反相求和电路
- 3.2.1 多个输入信号均加载在运放的反相端而同相端接地
- 3.2.2 具体电路分析自行看书,不再展开论述,实质上可以按照叠加原理或者直接运用理想集成运放的虚短虚断条件分析即可
- 3.3 同相求和电路
- 3.3.1 多个输入信号均加载在运放的同相端
- 3.3.2 具体电路分析自行看书,不再展开论述
- 3.4 加减求和电路
- 3.4.1 实际上拆分成同相求和电路(+)和反相求和电路(-)两部分分析即可;分别分析时,只需要将另外一端口的输入信号全部置零接地即可
- 3.5 平衡电路提醒
- 3.5.1 一般地该考点喜欢考电路设计,在实际设计时我们可以倾向于美的对称来设置电阻,这会极大节省时间
- 3.5.2 如前所述,集成运放可以视为一个高性能的差分放大电路,差分放大电路是参数一致理想对称的,因此在实际设计时,应当注意同相、反相端口电阻的总阻值相同,起到平衡电阻的作用
- 积分微分电路(要求不高)
- 4.1 积分电路
- 4.1.1 基本的,由电阻电容实现,电容接入反馈网络
- 4.1.2 鉴于考试要求不高,不深入展开分析,但需要知道基本电路形式
- 4.1.3 通过积分电路可以实现波形变换,例如将方波转为三角波、将正弦波转为余弦波等等
- 4.2 微分电路
- 4.2.1 基本的,由电阻电容实现,电阻接入反馈网络,电容与输入信号连接
- 4.2.2 鉴于考试要求不高,不深入展开分析,但需要知道基本电路形式
- 指数对数电路(要求不高)
- 5.1 指数电路
- 5.1.1 将二极管(或三极管)接入输入回路就可以实现基本指数运算
- 5.1.2 鉴于考试要求不高,不深入展开分析,但需要知道基本电路形式
- 5.2 对数电路
- 5.2.1 将二极管(或三极管)接入反馈网络就可以实现基本的对数运算
- 5.2.2 鉴于考试要求不高,不深入展开分析,但需要知道基本电路形式
- 比较器(必备)
- 6.1 综述
- 6.1.1 这里我们讲的比较器特别指电压比较器
- 6.1.2 在电压比较器电路中,集成运放需要工作在非线性区域,这就要求集成运放处于开环状态,或者引入正反馈
- 6.1.3 在比较器电路,对于集成运放而言,其虚断条件依然成立,但虚短条件不再成立.换言之,我们依然忽略电流净输入,但不能忽略电压净输入
- 6.1.4 比较器都存在阈值电压$U_{T}$,当变化经过阈值电压时,就会出现输出电压的跃变
- 6.2 分类:分为单限比较器、滞回比较器和窗口比较器
- 6.3 单限比较器
- 6.3.1 过零比较器
- 6.3.1.1 过零比较器是最简单的单限比较器,其阈值电压$U_{T}=0V$,运放处于开环状态
- 6.3.1.2 运放一端口连接输入信号,另一端口接地.当输入电压越过0V时,输出电压就会跃变
- 6.3.2 一般的单限比较器
- 6.3.2.1 依然是处于开环状态
- 6.3.2.2 考题中,首先需要计算出其阈值电压$U_{T}$,方法是寻求运放两个输入端电压$u_{P}$和$u_{N}$的表达式,并令$u_{P}=u_{N}$就能给出阈值电压
- 6.3.3 单限比较器具有很强的灵敏性,也因此其抗干扰能力很差
- 6.3.1 过零比较器
- 6.4 滞回比较器
- 6.4.1 滞回比较器相对于单限比较器而言,具备强的抗干扰性
- 6.4.2 滞回比较器电路引入正反馈
- 6.4.3 滞回比较器存在两个不同的阈值电压,电路中一般存在两个相对连接的稳压二极管
- 6.4.3 考题中,首先依然需要按照6.3.2.2的方式计算出两个阈值电压
- 6.4.4 运放输出端的接入的电阻一般是必不可少的,该电阻的作用是承载运放输出端与输出端间的压降
- 6.5 窗口比较器
- 6.5.1 有了上面的基础,看到题目自行分析即可
- 6.6 比较器的总结性综述
- 6.6.1 在电压比较器中,集成运放多工作在非线性区,输出只有高电平和低电平两种状态
- 6.6.2 解决问题的首要是计算阈值电压,图像的跃变方向与输入电压作用于同相还是反相输入端有关
- 方波发生器(建议必备)
- 7.1 最基本的电路
- 7.1.1 方波发生电路的构成:电压比较器电路、振荡电路和正反馈电路
- 7.1.2 具体下图中,由$R_{1},R_{2}$构成正反馈网络、由$R_{3},C$构成振荡网络、由运放,$R_{4}$和稳压二极管组成电压比较网络
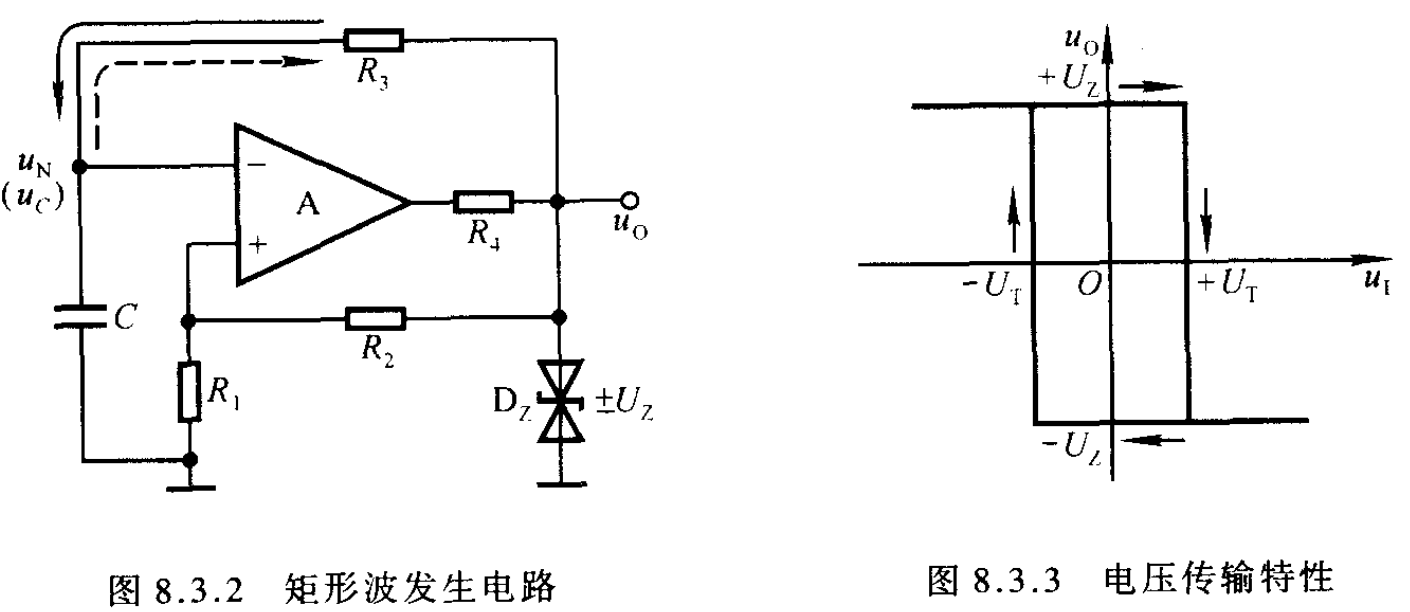
- 7.2 回顾:三要素法(必备)
- 7.2.1 时间常数$\tau$: $\tau=RC$,就是寻求电容所在回路的等效电阻
- 7.2.2 初值条件$U(t=0)$: 题目给出就更好,没给就自行假设一个可行的状态
- 7.2.3 边界条件$U(t=\infty)$: 电容充放电平衡时的理论最高电压
- 7.2.4 三要素方程:$U(t)=U(\infty)+[U(0)-U(\infty)]e^{-\frac{t}{\tau}}$
- 7.3 分析步骤(看习惯)
- 7.3.1 阈值电压:$u_{N}=u_{P}=\pm\frac{R_{1}}{R_{1}+R_{2}}U_{Z}=\pm\beta U_{Z}$
- 7.3.2 时间常数:$\tau=R_{3}C$
- 7.3.3 初值条件:没给,自行设定为$U(0)=-\beta U_{Z}$,回路图中为由$-U_{Z}$向$U_{Z}$的跃变
- 7.3.4 边界条件:$U(\infty)=U_{Z}$
- 7.3.5 边界条件:$U(\frac{T}{2})=\beta U_{Z}=U_{Z}-(1+\beta)U_{Z}e^{-\frac{T}{2R_{3 }C}}$
- 7.3.6 解方程得:$T=2R_{3}C\ln(1+\frac{2R_{1}}{R_{2}})$
- 7.4 进阶版:占空比可调的电路
- 7.4.1 占空比q:在一个周期中高平电压所占的比例
- 7.4.2 上图!
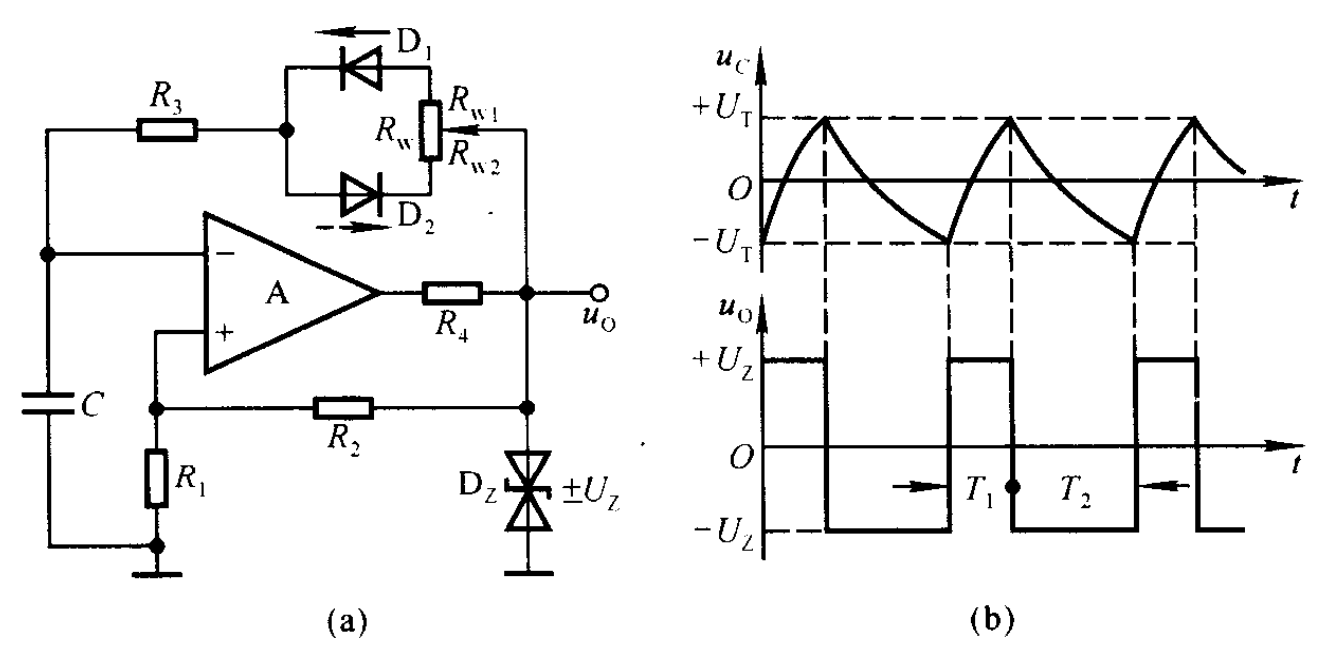
- 7.4.3 周期分析:设充电时长为$T_{1}$,放电时长为$T_{2}$,有了上面的基础,我们可以很容易的写出两个表达式分别为
$$\begin{aligned}
T_{1}&=(R_{3}+R_{w1})C\ln(1+\frac{2R_{1}}{R_{2}}) \\
T_{2}&=(R_{3}+R_{w2})C\ln(1+\frac{2R_{1}}{R_{2}}) \\
&\Rightarrow \\
T&=(R_{3}+R_{w})C\ln(1+\frac{2R_{1}}{R_{2}}) \\
q&=\frac{T_{1}}{T}=\frac{R_{3}+R_{w1}}{R_{3}+R_{w}}
\end{aligned}$$
- 三角波发生电路(了解)
- 8.1 前面说过通过积分运放电路可以实现由方波到三角波的波形转换
- 8.2 在7.方波发生电路中已经详细说明了如何产生方波,因此只需要在其基础上接入一个积分运算电路,就能利用产生的方波,作为积分运算电路的输入信号,实现三角波的输出
- 8.3 毕竟含有积分电路,应该不是很重点考点,不加详述了
- 电压-电流-电压转换电路(推荐)
- 9.1 上图!
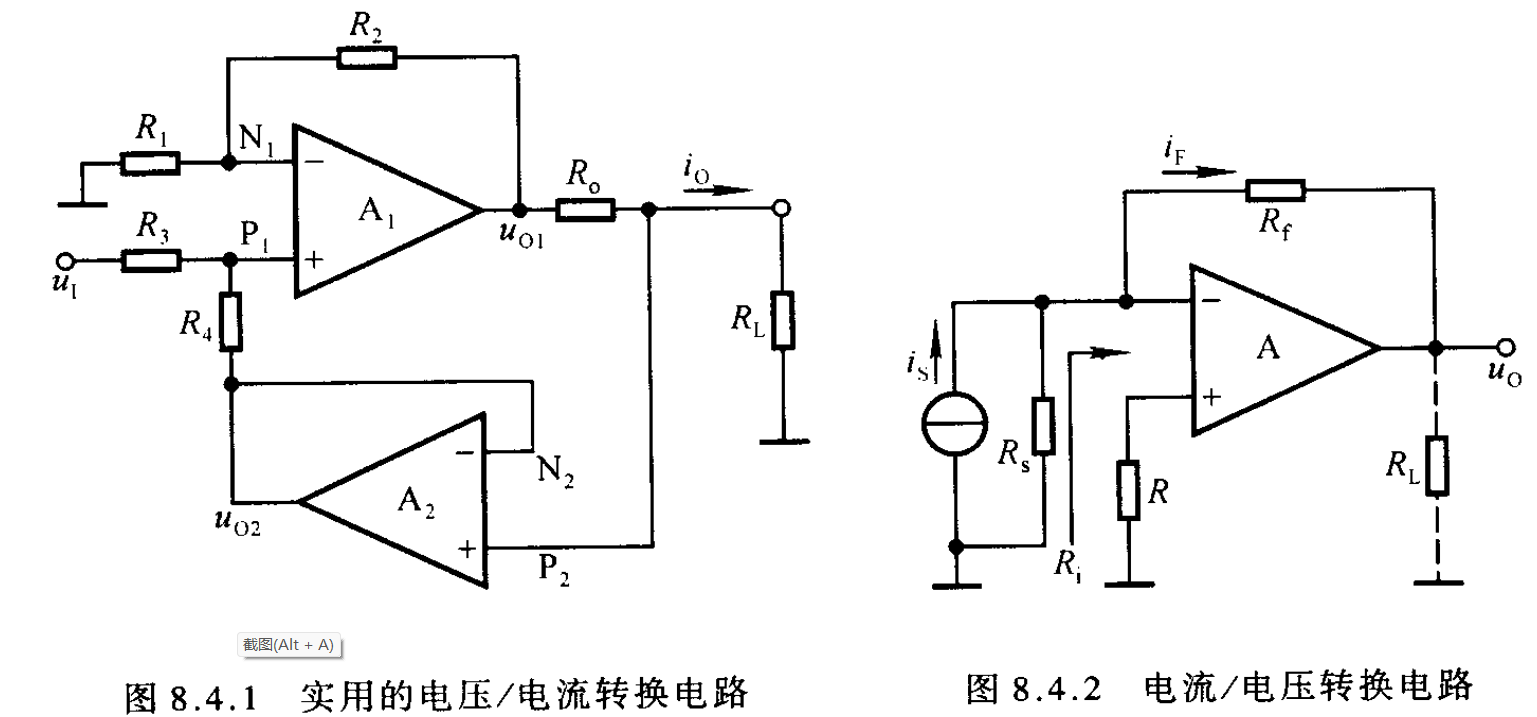
- 9.2 电压-电流转换电路
- 9.2.1 分析
考虑到考试的电路必然不会那么简单,遂以此为例
$R_{1}=R_{2}=R_{3}=R_{4}=R$
该电路由$A_{1}$运放所在的同相求和电路和$A_{2}$所在的射极跟随器组成
对射极跟随器显然有:$u_{P2}=u_{o2}$,于是$R_{4}$下方可以视为一个电压源替代
利用叠加原理可得:$u_{P1}=\frac{R_{4}}{R_{3}+R_{4}}u_{i}+\frac{R_{3}}{R_{3}+R_{4}}u_{o2}$
利用$A_{1}$虚短虚断的性质可得:$u_{o1}=(1+\frac{R_{2}}{R_{1}})u_{N1}$
利用欧姆定律可得:$i_{o}=\frac{u_{o1}-u_{P2}}{R_{o}}$
整理便得到:$i_{o}=\frac{u_{i}}{R_{o}}$
- 9.2.1 分析
- 9.3 电流-电压转换电路
- 9.3.1 分析
引入电压并联负反馈
利用虚短虚断可以快速得到$i_{S}=i_{F}$,于是$u_{o}=-i_{S}R_{f}$
- 9.3.1 分析
直流电源与整流电路
- 概念组
- 直流电源是将电网电压的交流电转换为直流电的能量转换电路
- 电容滤波电路适用于负载电流较小的情况
- 电感滤波电路适用于负载电流较大的情况
- 稳压管稳压电路中,限流电阻是必不可少的元件.限流电阻的作用是限制稳压管中的电流,使稳压管工作在稳压状态且不会损坏;同时在电网波动时产生相反的变化,起补偿作用,维持输出电压基本不变
- 整流电路(必备)
- 2.1 半波整流电路
- 2.1.1 上图
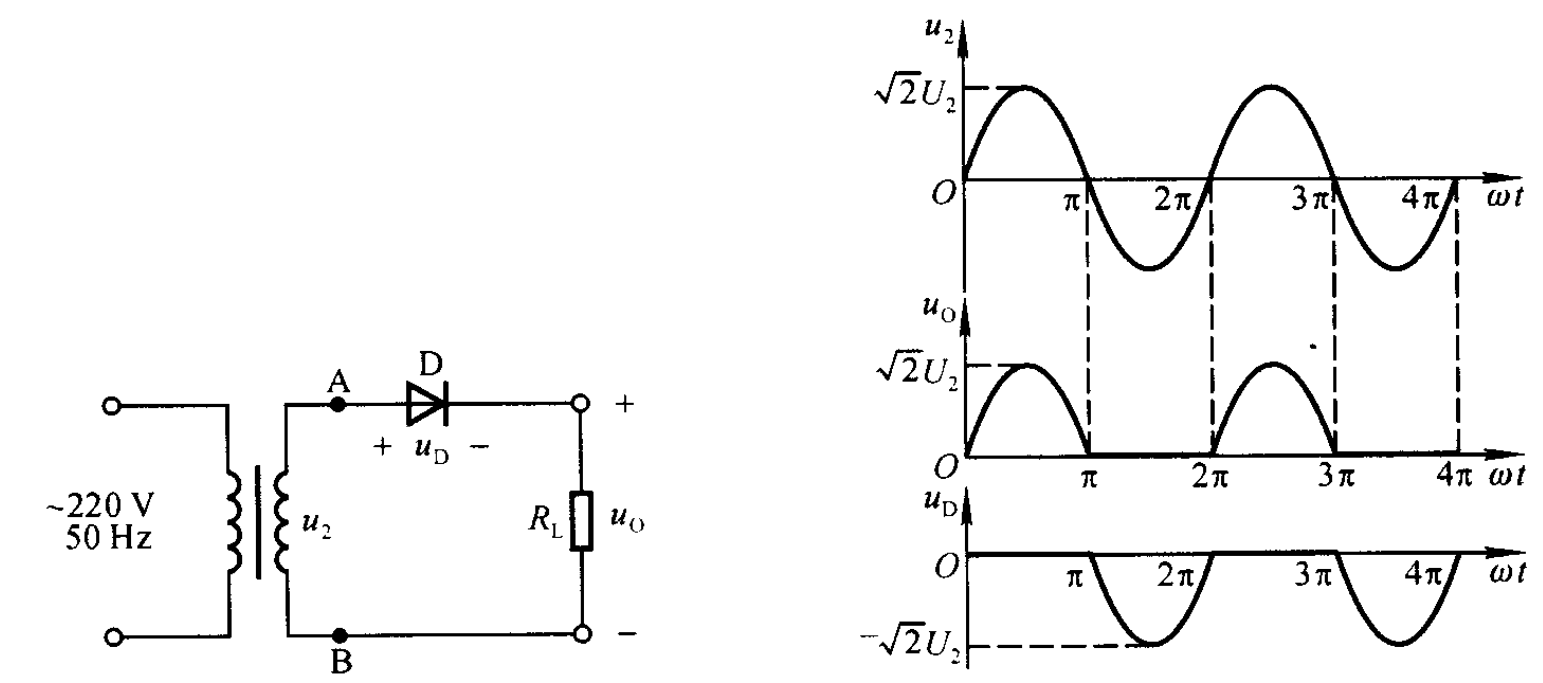
- 2.1.2 原理
显然只有正向电压时理想二极管才会导通,因此输出波形只有半个周期(理想二极管零导通开启电压) - 2.1.3 主要参数
- 2.1.3.1 平均输出电压
$$U_{o(AV)}=\frac{1}{2\pi}\int_{0}^{\pi}\sqrt{2}U_{2}\sin(\omega t)\mathrm{d\omega t}=\frac{\sqrt{2}}{\pi}U_{2}=0.45U_{2}$$ - 2.1.3.2 脉动系数S:基波峰值与输出电压平均值之比
$$\begin{aligned}
S=\frac{\pi}{2}=1.57
\end{aligned}$$ - 2.1.3.3 最大反向电压和最大平均电流
一般情况下,允许电网存在10%的波动,因此选取二极管时需要留心其最大允许的反向电压和允许的最大电流
对半波整流电路,最大反向电压为$U_{max}=1.1\sqrt{2}U_{2}$
对半波整流电路,最大平均电流为$I_{F}=1.1\frac{\sqrt{2}U_{2}}{\pi R}$
- 2.1.3.1 平均输出电压
- 2.1.1 上图
- 2.2 全波整流电路
- 2.2.1 全波整流电路就实现了完全利用整个信号周期
- 2.2.2 主要参数
- 2.2.2.1 平均输出电压
$$U_{o(AV)}=\frac{1}{\pi}\int_{0}^{\pi}\sqrt{2}U_{2}\sin(\omega t)\mathrm{d\omega t}=\frac{2\sqrt{2}}{\pi}U_{2}=0.9U_{2}$$ - 2.2.2.2 脉动系数
$$\begin{aligned}
S=\frac{2}{3}=0.67
\end{aligned}$$ - 2.2.2.3 最大反向电压和最大平均电流
$U_{max}=1.1\sqrt{2}U_{2}$
$I_{F}=1.1\frac{2\sqrt{2}U_{2}}{\pi R}$
- 2.2.2.1 平均输出电压
- 2.3 桥式整流电路
- 2.3.1 上图
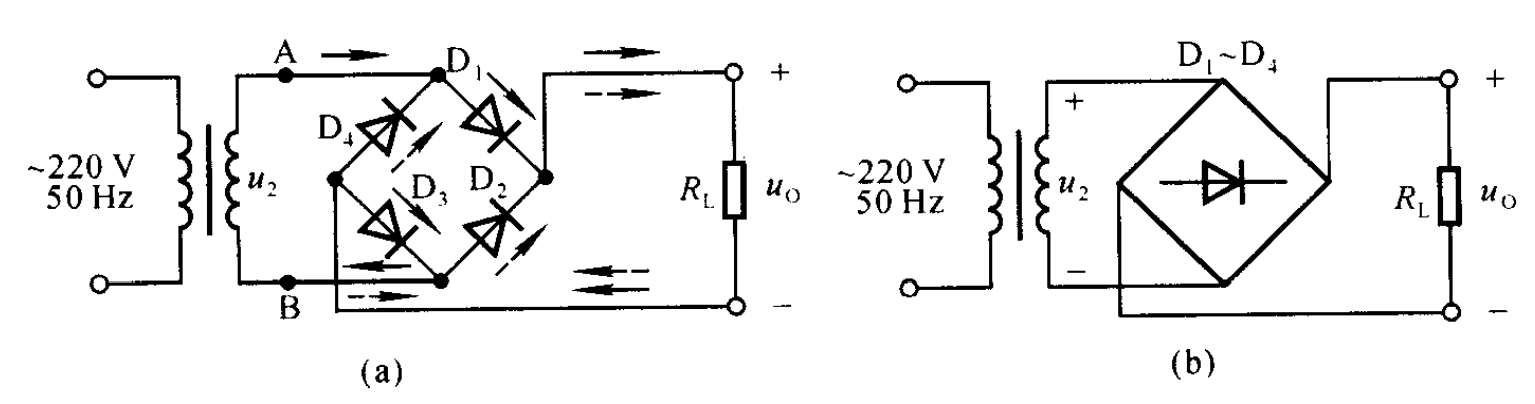
- 2.3.2 主要参数
- 2.3.2.1 平均输出电压
$$U_{o(AV)}=\frac{1}{\pi}\int_{0}^{\pi}\sqrt{2}U_{2}\sin(\omega t)\mathrm{d\omega t}=\frac{2\sqrt{2}}{\pi}U_{2}=0.9U_{2}$$ - 2.3.2.2 脉动系数
$$\begin{aligned}
S=\frac{2}{3}=0.67
\end{aligned}$$ - 2.3.2.3 最大反向电压和最大平均电流
$U_{max}=1.1\sqrt{2}U_{2}$
$I_{F}=1.1\frac{2\sqrt{2}U_{2}}{\pi R}$
- 2.3.2.1 平均输出电压
- 2.3.3 肉眼清晰地可见与全波整流是一致的
- 2.3.1 上图
- 滤波电路
- 3.1 电容滤波电路
- 3.1.1 上图
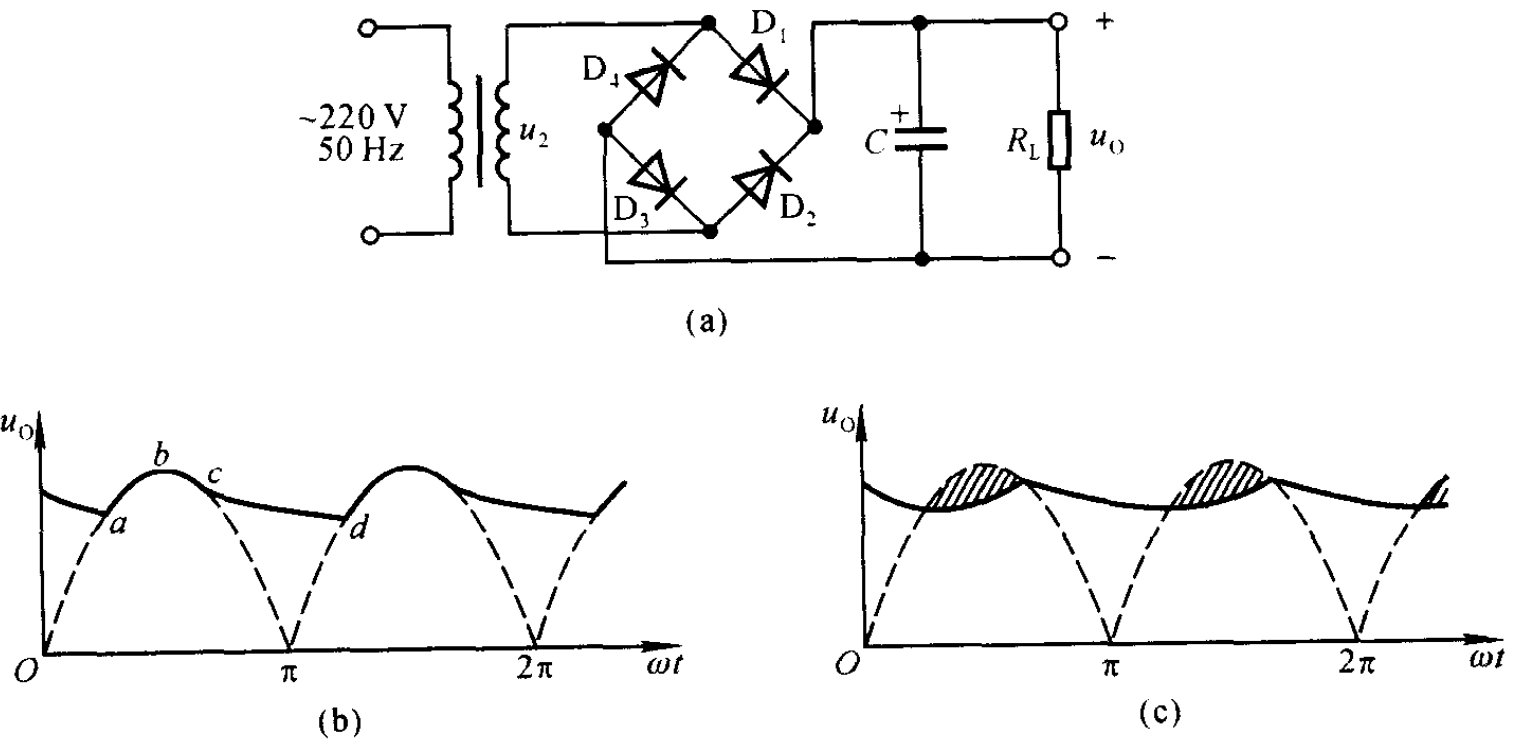
- 3.1.2 结构
最简单的滤波电路就是在桥式整流电路后面并联一个电容
电容滤波电路利用电容的充放电作用,使输出电压趋于平滑 - 3.1.3 原理
都是理想二极管奥,因此,零正向压降
当电压$u_{2}$处于正半周并且数值大于电容两端的电压时,电流一路流经电容,给电容充电;另一路流经负载电阻,并且理想变压器无损耗,加之理想二极管无正向压降,因此$u_{2}=u_{c}=u_{o}$成立.当$u_{2}$增大时输出电压随之增大;当其减小时,电容通过负载放电,电容电压下降,下降趋势与$u_{2}$基本相同.但是电容器是按照指数规律放电,当$u_{2}$下滑到一定程度时,$u_{c}$的变化慢于$u_{2}$因此二极管$D_{1},D_{3}$截止,此后电容通过负载放电;当副线圈电压处于负半周并大于电容电压时,重复上述过程即可. - 3.1.4 上图
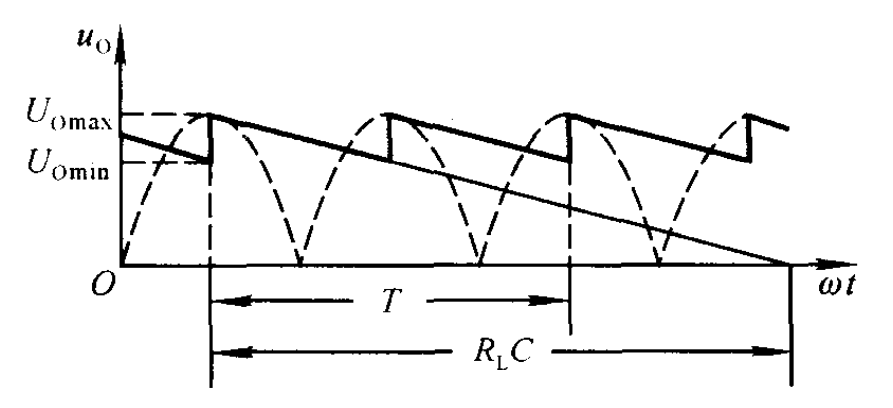
- 3.1.5 主要参量
我们认为电容每次充放电都能达到$u_{2}$的峰值,即$U_{omax}=\sqrt{2}U_{2}$,且在半周期$\frac{T}{2}$时达到最小值$U_{omin}$.
因此输出电压的平均值为:$U_{o(AV)}=\frac{U_{omax}+U_{omin}}{2}$
根据相似关系可知
$$\frac{T}{2R_{L}C}=\frac{U_{omax}-U_{omin}}{U_{omax}}$$
最终可以得到
$$\begin{aligned}
U_{o(AV)}=\sqrt{2}U_{2}(1-\frac{T}{4R_{L}C})
\end{aligned}$$
当负载开路时,$U_{o(AV)}=\sqrt{2}U_{2}$
当$R_{L}C=(3-5)\frac{T}{2}$时,$U_{o(AV)}=1.2U_{2}$
电容的最低耐压值为:$U=1.1\sqrt{2}U_{2}$
脉动系数S:$S=\frac{T}{4R_{L}C-T}$
- 3.1.1 上图
- 稳压管稳压电路
- 4.1 上图
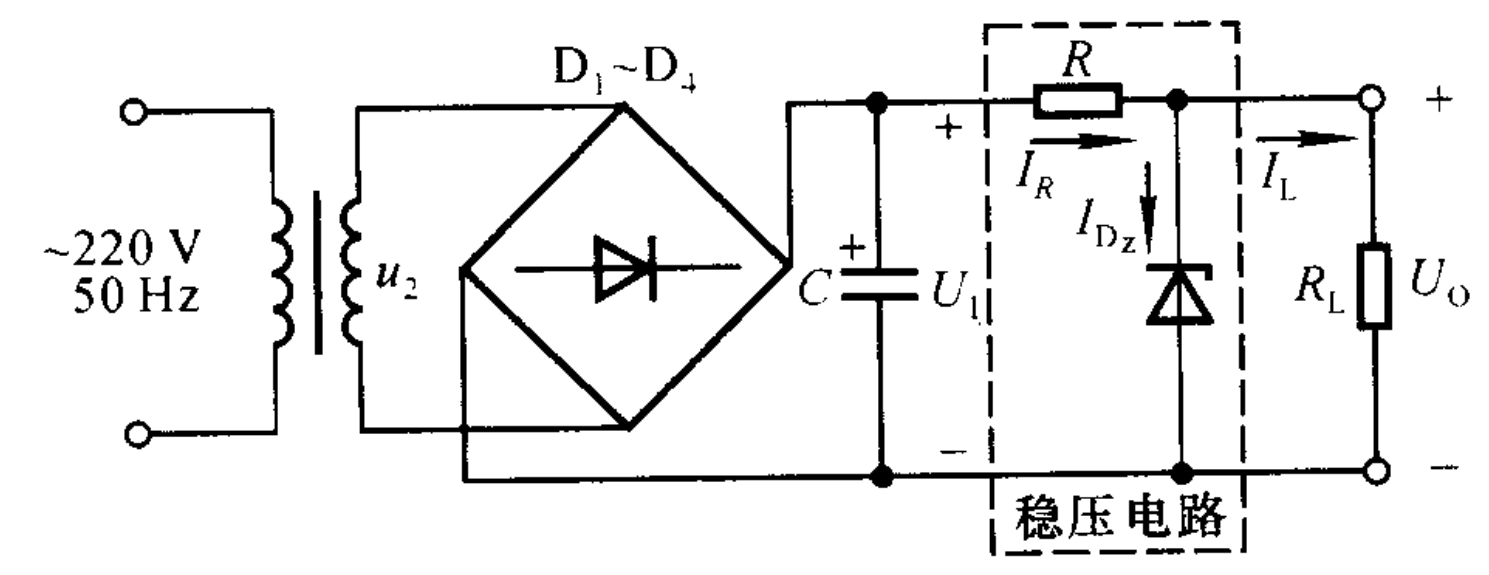
- 4.2 稳压原理
当电网电压增大时,滤波电路的输出电压也随之增大,最终输出电压也随之增大.但由于稳压二极管需满足$U_{O}=U_{Z}$,$U_{Z}$增大必然导致通过稳压二极管的电流$I_{DZ}$增大,因而降落在电阻R上的电压增大,这就使得$U_{O}$减小,从而实现最终输出电压基本不变 - 4.3 电阻R的作用
通过分析可以看出,利用稳压二极管的电流调节作用,通过限流电阻R上的电流或电压实现补偿,达到稳压的目的.因此限流电阻R必不可少
- 串联型稳压电路
- 5.1 前言
在4.稳压电路中,我们看到利用稳压二极管就能实现输出电压的稳定输出,但是通过稳压二极管的电流变化幅度较小,稳压二极管正常工作,其电流必须不小于最小稳压电流、不大于最大稳压电流,即$I_{Z}<I_{DZ}<I_{ZM}$;此外其输出电压不可调节也是一大缺陷 - 5.2 上图
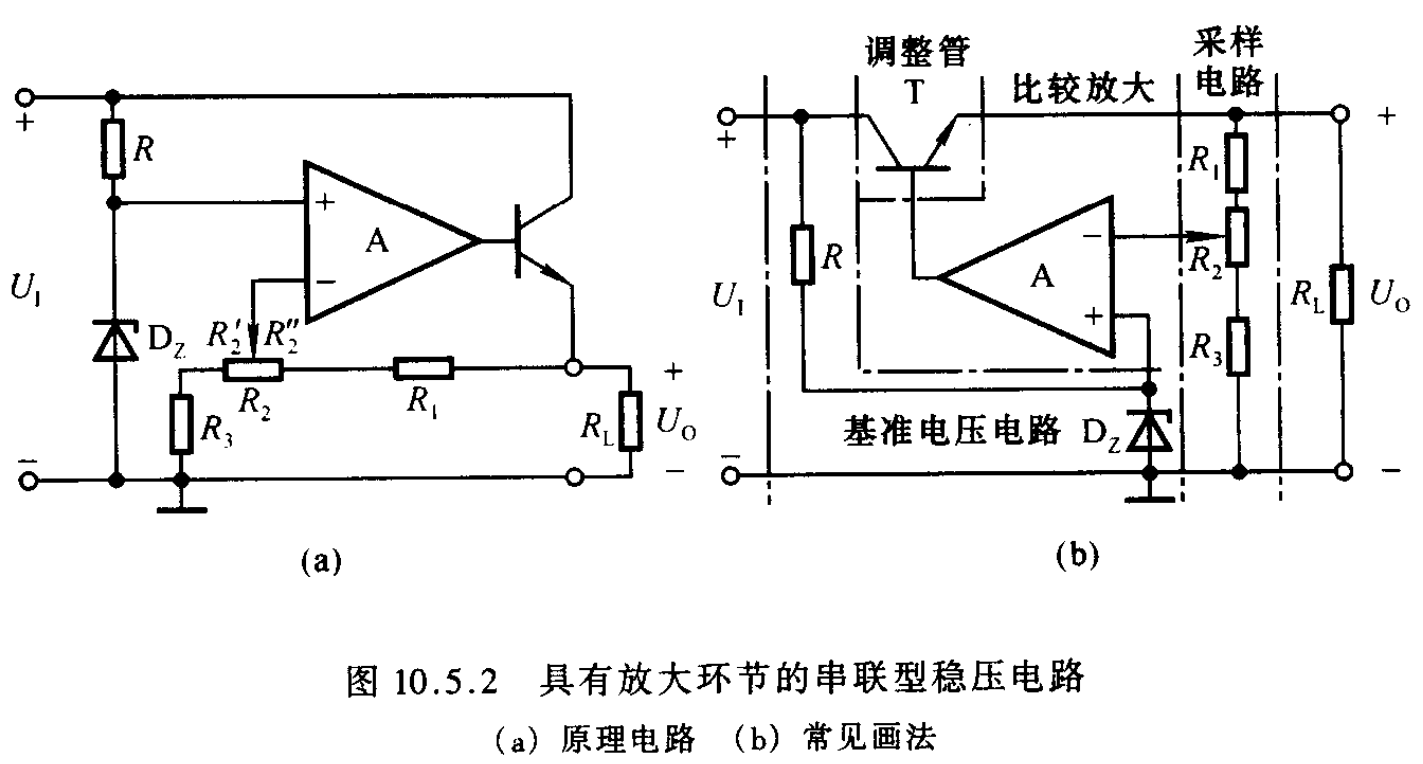
- 5.3 原理
设想当因为电网波动使输出电压升高时,这一变化将通过由$R_{1}、R_{2}、R_{3}$组成的采样电路反馈到运放的反相端;运放的同相端电位基本为稳压管的电压;这样运放的输出电压,也即为晶体管的基极电压,$U_{o}=A_{d}(u_{P}-u_{N})$势必降低.由于晶体管采取射极输出(基极与射极的变化同相的),于是$U_{o}$的电压也势必降低,从而使输出电压稳定
电路是靠引入深度电压负反馈来稳定输出电压的 - 5.4 输出电压的调整范围
利用理想运放深度负反馈满足的虚短虚断条件容易得到:
$$U_{Z}=u_{P}=u_{N}=\frac{R_{3}+R_{2}’}{R_{1}+R_{2}+R_{3}}U_{o}$$
因此调节范围显然为
$$\begin{aligned}
\frac{R_{1}+R_{2}+R_{3}}{R_{2}+R_{3}}U_{Z}\le U_{o} \le\frac{R_{1}+R_{2}+R_{3}}{R_{3}}U_{Z}
\end{aligned}$$ - 5.5 正常稳压时调整管满足的条件
整个电路中调整管(晶体管)是核心元件,其应工作在放大区,因此可以得到约束条件为
$$U_{CE(min)}>U_{CES}$$
而管压降的最小值,显然是在当供给给集电极电压最小而射极的输出电压值最大时产生的
$$\begin{aligned}
U_{E(max)}=U_{O(max)}
\end{aligned}$$
对与$U_{C(min)}$,则需要根据前面连接的电路是电容滤波电路,还是桥式整流电路,抑或是其他电路,进行具体分析
THE END
您阅读这篇文章共花了:

Invitation
Floral-Sunsunrise
FeynmanDirac
created:12/03/2022
Welcome to Floral-Sunsunrise
This is an identification card as an honored membership of FeynmanDirac
Happy to see you follow FeynmanDirac, enjoy science together
© 版权声明
 验证码启动中...
验证码启动中...
备用人机验证