Wave optics
请注意,本文最近一次更新于:2022-03-12,文章内容可能已经不具有时效性,请谨慎参考
本文最后更新于:2022年3月12日星期六晚上6点16分 +08:00
本文简要概述波动光学的相关知识,由于覆盖不全,将持续更新
光波场
- 光是交变电磁场
- 光具有时间和空间两重周期性
- 定态光波的概念
- 满足如下条件的波场为定态波场
- 波场空间中各点的扰动是同频率的简谐振动
- 波场中各点扰动的振幅只与空间位置有关而与时间无关
- 满足如下条件的波场为定态波场
- 光是矢量波
- 光波的传播方向可以用一个矢量表示,称为波矢
$$\begin{aligned}
\vec{k} = \frac{2\pi}{\lambda}\vec{s}
\end{aligned}$$
$\vec{s}$是传播方向上的单位矢量 - 在真空和各向同性均匀介质中,电场矢量$\vec{E}$、磁感应矢量$\vec{B}$、波矢$\vec{k}$是两两正交的,且场矢量$\vec{E}$、磁感应矢量$\vec{B}$是同相位的.
- 平面波和球面波的矢量表达式分别如下
$$
\left{\begin{aligned}
\vec{E}(\vec{r},t) = E_0(\vec{r})\cos (\vec{k}\cdot\vec{r} - \omega t + \varphi_0)
&\
\vec{B}(\vec{r},t) = B_0(\vec{r})\cos (\vec{k}\cdot\vec{r} - \omega t + \varphi_1)
\end{aligned}
\right.
$$
$$
\left{\begin{aligned}
\vec{E}(\vec{r},t) = \frac{E_0}{\vec{r}}(\vec{r})\cos (\vec{k}\cdot\vec{r} - \omega t + \varphi_0)
&\
\vec{B}(\vec{r},t) = \frac{B_0}{\vec{r}}(\vec{r})\cos (\vec{k}\cdot\vec{r} - \omega t + \varphi_1)
\end{aligned}
\right.
$$
- 光波的传播方向可以用一个矢量表示,称为波矢
- 光强
- 电磁场具有能量,而且传输能量,电磁场的能量可以用能流密度描述
- 能流密度:
- 能流密度是指单位时间内通过垂直于传播方向单位面积的能量,能流密度是一个矢量,其方向表示电磁场能量传输的方向.这个矢量被称为坡印廷矢量
$$\begin{aligned}
\vec{S} = \vec{E}\times\vec{H}
\end{aligned}$$ - 根据能流密度与能量密度的关系(根据两者定义脑补模型即可,此处不再配图详尽推导)
$$\begin{aligned}
\vec{S} = w\vec{v} = \frac{\vec{v}}{2}(\epsilon E^2 + \mu H^2)
\end{aligned}$$ - 由于光的频率很高而现有探测器的反应时间远比光的传播周期长,因此探测到的能流密度实际上都是在一段时间内的平均值.光的强度是光波场平均能流密度的绝对值,也就是平均坡印廷矢量的绝对值.
$$\begin{aligned}
I = <\lvert \vec{S} \rvert> = <\lvert \vec{E}\times\vec{H} \rvert>
\end{aligned}$$
在各向同性的无源介质中,对上式计算可以得到
$$\begin{aligned}
I = <\lvert \vec{E}\times\vec{H} \rvert>
\ = <\lvert \vec{E}\times\frac{\vec{B}}{\mu} \rvert>
\ = <\lvert \vec{E}\times\frac{\vec{k}}{\omega}\times\vec{E} \rvert>
\ = \frac{1}{T}\int_0^T \frac{k}{\omega \mu}E^2\mathrm{d}t
\ = \frac{E^2_0}{2}\sqrt{\frac{\epsilon}{\mu}}
\ = \frac{nE^2_0}{2c\mu}
\end{aligned}$$
在不考虑量纲的情况下
$$\begin{aligned}
I \propto nE_0^2 \propto E_0^2
\end{aligned}$$ - 光的电场强度也称为光矢量
- 能流密度是指单位时间内通过垂直于传播方向单位面积的能量,能流密度是一个矢量,其方向表示电磁场能量传输的方向.这个矢量被称为坡印廷矢量
定态波场的数学描述
平面波
- 平面波具有以下特征
- 振幅是常数
- 空间相位是直角坐标的线性函数
$$\begin{aligned}\varphi(\vec{P}) = \varphi_0 + \vec{k}\cdot\vec{r} = k_1x + k_2y + k_3z + \varphi_0\end{aligned}$$ - 波的余弦表达式为
$$\begin{aligned}
E(\vec{r},t) = E_0(\vec{r})\cos(\vec{k}\cdot\vec{r} - \omega t + \varphi_0)
\end{aligned}$$
由于$\vec{k}\cdot\vec{r}$ = const,从数学上解释可以发现该式表示一系列与波矢垂直的平面.球面波
- 球面波具有以下特征
- 场点P处的振幅为
$$\begin{aligned}
A(\vec{P}) = \frac{a}{r}
\end{aligned}$$
某点出的振幅与到波源的距离成反比,振幅随位矢范数增大而衰减. - 空间相位是球面对称的
$$\begin{aligned}
\varphi(\vec{P}) = kr + \varphi_0 = const
\end{aligned}$$ - 球面波方程
$$\begin{aligned}
E(\vec{r},t) = \frac{a}{\vec{\lvert r \rvert}}\cos(\vec{k}\cdot\vec{r} - \omega t + \varphi_0)
\end{aligned}$$柱面波
- 场点P处的振幅为
- 柱面波具有以下特征
- 振幅表征
$$\begin{aligned}
A(\vec{P}) = \frac{a}{\sqrt{r}} \quad (r为圆柱面的半径)
\end{aligned}$$ - 空间相位
$$\begin{aligned}
\varphi(\vec{P}) = kr + \varphi_0
\end{aligned}$$ - 振动表达式
$$\begin{aligned}
E(\vec{r},t) = \frac{a}{\sqrt{\vec{\lvert r \rvert}}}\cos(\vec{k}\cdot\vec{r} - \omega t + \varphi_0)
\end{aligned}$$
- 振幅表征
傍轴条件与远场条件
傍轴近似
- 设想一发光点在坐标轴原点,接受屏垂直于Z轴且与物体所在的垂直距离为z,接受屏上存在一点P,与接受屏对与Z轴交点的距离为r,此时球面波的振幅为
$$\begin{aligned}
A(\vec{P}) = \frac{a}{\sqrt{z^2 + r^2}}
\end{aligned}$$
幂展开可以得到
$$\begin{aligned}
A(\vec{P}) = \frac{a}{z(1 + \frac{1}{2}(\frac{r}{z})^2 + …)}
\end{aligned}$$
如果满足r << z,则高次展开可以忽略,因此
$$\begin{aligned}
A(\vec{P}) = \frac{a}{z}
\end{aligned}$$
满足r << z称为傍轴条件远场近似
- 在上面的模型中,球面波在接受屏幕上的相位为
$$\begin{aligned}
\varphi(\vec{P}) = k\sqrt{z^2 + r^2}
\= kz(1 + \frac{1}{2}(\frac{r}{z})^2 + …)
\= k(z + \frac{1}{2}\frac{r^2}{z} + …)
\end{aligned}$$
如果满足
$$\begin{aligned}
z >> \frac{r^2}{\lambda}
\end{aligned}$$
则高次项可以忽略,因此
$$\begin{aligned}
\varphi(\vec{P}) = kz
\end{aligned}$$
上述条件称为远场条件,满足远场条件必然满足傍轴条件
光的叠加原理
- 成立条件
介质为线性介质且振动不是十分强烈,振动很强烈时线性介质会变成非线性介质 - 叠加的具体过程已经在前面的机械波中有过推导,这里不再赘述.仅仅给出相关结论
- 不同频率的光是不相干的
- 频率相近的单色光叠加形成光学拍
- 不同频率的定态光波叠加得到非定态光
- 振动方向垂直的光非相干且总光强为两光强之和
- 根据省略的推导分析我们得出相干光产生的条件
- 相位差恒定
- 存在互相平行的振动分量
- 频率相同
光的偏振性
- 光波是电磁波,其电场强度、磁感应强度和波矢互相垂直,因此光波是横波.因可见光波段的电磁波不会引起大多数介质的磁化,因此只考虑其光矢量(即电矢量)
- 横波的振动方向与传播方向垂直,往往会表现出偏振特性.偏振,是振动方向相对于传播方向的不对称性,其表现为虽然在各个方向上存在振动但是不同方向上的振幅不同或者电矢量只在一个平面内有振动.
马吕斯定理
- 马吕斯定律指出,光线束在各向同性的均匀介质中传播时,始终保持着与波面的正交性,并且入射波面与出射波面对应点之间的光程均为定值
- 马吕斯定理指出通过偏振片后光强关系满足
$$\begin{aligned}
I = I_0 \cos^2 \alpha
\end{aligned}$$
$\alpha$是入射线偏振光的光振动方向和偏振片偏振化方向之间的夹角
应当指出的是,自然光通过起偏器后的光强变为原来的一半,下面简要证明
$$\begin{aligned}
I = \int_0^{2\pi} (E_0\cos\theta)^2\mathrm{d}\theta
\ = \frac{1}{2}E^2_0 = \frac{1}{2}I_0
\end{aligned}$$偏振光的分类
- 平面偏振光(线偏振光)
- 自然光经过起偏器后,由于只有平行于起偏器偏振化方向的电矢量才能通过,因此透射光只包含单一振动方向的电矢量,这种矢量始终在同一个平面内振动,投影上看来,电矢量只是一条直线,这样的光就是线偏振光(平面偏振光)
- 任何一个平面偏振光,都可以分解为两个振动面互相正交的平面偏振光
- 我们用消光比来描述偏振仪器的起偏效果,消光比表示为
$$\begin{aligned}
消光比 = \frac{最小透射光强}{最大透射光强} = \frac{I_{min}}{I_{max}}
\end{aligned}$$
- 圆偏振光
- 在一个与光传播方向(波矢方向)垂直的平面内观察其电矢量,如果光的电矢量不是在一个固定的平面内振动,而是绕着传播方向匀速旋转,并且旋转过程中电矢量的大小不发生改变,这就是圆偏振光.
- 根据光的叠加原理可知,圆偏振光可以分解为两个相互正交的平面偏振光,且这两个平面偏振光存在$\frac{\pi}{2}$的相位差.
- 迎着光的传播方向观察,如果光矢量(电矢量)是顺时针旋转的,则称为右旋圆偏振光;如果电矢量是逆时针旋转的,则称为左旋圆偏振光
- 同一个空间位置的圆偏振光可以表示为
$$
\begin{equation}
\left{\begin{aligned}
E_x(z,t) = A\cos(\omega t)
&\
E_y(z,t) = A\cos(\omega t ± \frac{\pi}{2})
\end{aligned}
\right.
\end{equation}
$$
- 椭圆偏振光
- 与圆偏振光的定义类似,但是矢量端点的轨迹不再是圆,而是椭圆.
- 同样地,椭圆偏振光的电矢量也可以进行正交分解(同一位置省去了空间相位)
$$
\begin{equation}
\left{\begin{aligned}
E_x(z,t) = A\cos(\omega t)
&\
E_y(z,t) = A\cos(\omega t ± \Delta \varphi)
\end{aligned}
\right.
\end{equation}
$$
下面到了小把戏时刻
$$
\begin{equation}
\left{\begin{aligned}
\frac{E_x}{A_x} = \cos \omega t
&\
\frac{1}{\sin \Delta \varphi}(\frac{E_y}{A_y}-\cos\omega t\cos\Delta\varphi) = \sin\omega t
\end{aligned}
\right.
\end{equation}
$$
再进行一次小把戏就可以得到
$$\begin{aligned}
\frac{E^2_x}{A^2_x} + \frac{E^2_y}{A^2_y} - \frac{2E_x E_y}{A_x A_y}\cos\Delta\varphi = \sin^2\Delta\varphi
\end{aligned}$$
经过两次小把戏我们就得到了一个xoy平面内的椭圆方程!不过显然这个椭圆方程并不是标准方程,而是出现了偏心.椭圆的长轴或短轴对坐标轴的夹角满足
$$\begin{aligned}
\tan 2\alpha = \frac{2A_x A_y}{A^2_x-A^2_y}\cos\Delta\varphi
\end{aligned}$$
- 部分偏振光
- 部分偏振光是相对于传播方向就不呈轴对称性而是有一个优越的振动方向.即这种偏振光的电矢量在不同的方向上有不同的大小,其中有两个相互垂直的方向上电矢量的振幅分别为最大和最小.自然光经过反射或折射一般变成部分偏振光,自然光经过散射一般也会变成部分偏振光.
- 我们定义部分偏振光的偏振度P为
$$\begin{aligned}
P = \frac{I_{max} - I_{min}}{I_{max} + I_{min}}
\end{aligned}$$
应当指出的是自然光的偏振度为零,而平面偏振光的偏振度为1.
- 总结综述
- 从上面的讨论我们可以看出,平面偏振光、圆偏振光、椭圆偏振光的光矢量(电矢量)都可以看作是两个正交的分量叠加,分量的一般表达形式为:
$$\begin{cases}
E_x = A_x\cos(\omega t)
\
E_y =A_y\cos(\omega t + \Delta \varphi)
\end{cases}$$ - 当$\Delta \varphi$ = 0 或 $\pi$ 时上述方程演变为平面偏振光的方程
- 当$\Delta \varphi$ = $±\frac{\pi}{2}$ 且 $A_x = A_y$时,方程演变为圆偏振光
- 其余情况下的方程均是椭圆偏振光方程,由此,椭圆偏振光是更一般的偏振态
- 从上面的讨论我们可以看出,平面偏振光、圆偏振光、椭圆偏振光的光矢量(电矢量)都可以看作是两个正交的分量叠加,分量的一般表达形式为:
光与物质的相互作用
光的吸收
- 线性吸收的实验定律
- 实验表明在光强不是很大的情况下,在透明介质中,被吸收的光强与吸收体的厚度成正比.在各向同性的均匀介质中取一薄层,厚度为$\mathrm{d}x$,光射入薄层前的光强为I,从薄层射出后,强度为I + $\mathrm{d}I$, 则有
$$\begin{aligned} \mathrm{d}I = -\alpha I \mathrm{d}x \end{aligned}$$
解该常微分方程得
$$\begin{aligned}
I = I_0e^{-\alpha x}
\end{aligned}$$
系数$\alpha$是与介质有关得常数,称为吸收系数.上述实验定律称为布格尔定律或者朗伯定律
在溶液中,上述定律依然成立,但是吸收系数与溶液的浓度成正比
$$\begin{aligned}
\alpha = AC
\end{aligned}$$
C为溶液的浓度,A是与溶液有关的常数,这一定律称为比尔定律
- 实验表明在光强不是很大的情况下,在透明介质中,被吸收的光强与吸收体的厚度成正比.在各向同性的均匀介质中取一薄层,厚度为$\mathrm{d}x$,光射入薄层前的光强为I,从薄层射出后,强度为I + $\mathrm{d}I$, 则有
- 吸收系数$\alpha$与波长的关系
- 色散规律
- 散射现象
入射光与介质中的带电粒子相互作用,带电粒子在入射光的激发下做受迫振动,发出电磁波.这是有真实扰动源的光波,也称为次波.如果介质是均匀的,所发出的电磁波经过叠加后总有确定的方向,因此除了沿着入射光原来的方向有光继续传播之外其余方向均无光;而如果介质是不均匀的,则介质中发出的次波在其他方向上不能完全抵消,因此可以向任意方向传播,这就形成散射.光在密度不均匀的介质中总能产生散射 - 散射定律
- 瑞利散射
- 散射体尺寸小于入射波长
- 散射光强与入射光波长的四次方成反比$I \propto \lambda^{-4}$
- 德拜散射
- 散射体尺寸大于光波波长
- 散射光强对光波长依赖性不强,各个波长的散射光强差别不大
- 瑞利散射
光的干涉
杨氏双缝干涉
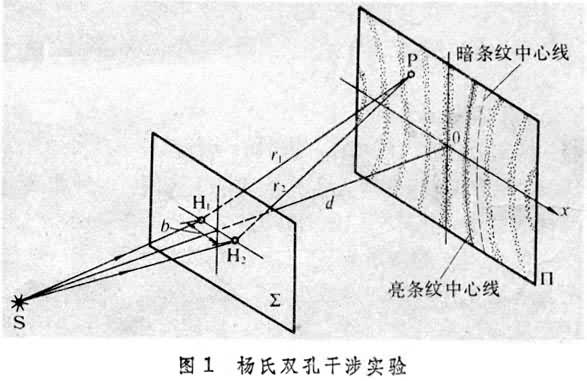
根据光的叠加原理,干涉光在某一点的光强为
$$\begin{aligned}
I = A^2_1 + A^2_2 + 2A_1A_2\cos(\Delta \varphi)
\end{aligned}$$
相位差$\Delta \varphi$ = $\Delta \varphi_0 + \frac{\Delta L}{\lambda}2\pi$,$\Delta L$是两光源对同一点的光程差,右式前项为两光源的初相位差.在杨氏双缝干涉实验中的两个光源是在同一个波阵面上,因此初相位为零.
第一个光源到某点的距离为:
$$\begin{aligned}
r^2_1 = D^2 + (x-\frac{d}{2})^2 + y^2
\end{aligned}$$
第二个光源到某点的距离为:
$$\begin{aligned}
r^2_2 = D^2 + (x+\frac{d}{2})^2 + y^2
\end{aligned}$$
考虑傍轴条件和远场条件近似得到
$$\begin{aligned}
r_1 = D + \frac{(x-\frac{d}{2})^2 + y^2}{2D}
\end{aligned}$$
$$\begin{aligned}
r_2 = D + \frac{(x+\frac{d}{2})^2 + y^2}{2D}
\end{aligned}$$
光程差为
$$\begin{aligned}
\Delta L = \frac{dx}{D}
\end{aligned}$$
因此亮条纹条件是
$$\begin{aligned}
\frac{dx}{D} = k\lambda ,k = 0,±1,±2…
\end{aligned}$$
暗纹条件是
$$\begin{aligned}
\frac{dx}{D} = (2k+1)\frac{\lambda}{2} ,k = 0,±1,±2…
\end{aligned}$$
- 干涉条纹的可见度(反衬度)
前面我们在偏振中定义了消光比,可见度(反衬度)在表达式上与之相同,可见度$\gamma$定义为
$$\begin{aligned}
\gamma = \frac{I_{max} - I_{min}}{I_{max} + I_{min}} = \frac{2A_1A_2}{A^2_1 + A^2_2}
\end{aligned}$$ - 两列平行光的干涉
前面的杨氏双缝干涉是同一个波阵面上的波源发出的相干光干涉叠加,其振幅和初相位均相同,这里我们讨论更为一般的情况.
设两列同频率的单色光的振幅分别为$A_1$,$A_2$;初相位分别为$\varphi_1$,$\varphi_2$,两列波的波矢方向分别为($\alpha_i$,$\beta_i$,$\gamma_i$),两列光在XOY平面上某一点的相位差为
$$\begin{aligned}
\Delta \varphi(x,y) = \vec{k}\cdot(\vec{r_1} - \vec{r_2}) + \varphi_1 - \varphi_2 =k(\cos\alpha_1-\cos\alpha_2)x+k(\cos\beta_1 - \cos\beta_2)y + \varphi_1 - \varphi_2
\end{aligned}$$
在该点的光强为
$$\begin{aligned}
I(x,y) = A^2_1+A^2_2+2A_1A_2\cos(\Delta \varphi)
\end{aligned}$$
前面我们定义了干涉条纹的反衬度(可见度)$\gamma$,因此上式也可以写为
$$\begin{aligned}
I(x,y) = (A^2_1+A^2_2)(1 + \gamma \cos(\Delta \varphi))
\end{aligned}$$- 由相位差确定的亮暗干涉条纹的条件为
$$
k(\cos\alpha_1-\cos\alpha_2)x+k(\cos\beta_1 - \cos\beta_2)y + \varphi_1 - \varphi_2 =
\begin{cases}
2k\pi
\
(2k+1)\pi
\end{cases}$$ - 上式方程显然是直线方程,因此亮暗条纹都是等间隔的平行直线,条纹间隔为
$$\begin{cases}
\Delta x = \frac{2\pi}{k(\cos\alpha_1 - \cos\alpha_2)} = \frac{\lambda}{\cos\alpha_1 - \cos\alpha_2}
\
\Delta y = \frac{2\pi}{k(\cos\beta_1 - \cos\beta_2)} = \frac{\lambda}{\cos\beta_1 - \cos\beta_2}
\end{cases}$$
- 由相位差确定的亮暗干涉条纹的条件为
洛埃镜
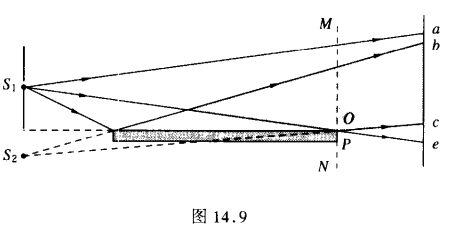
- 如上图所示,光源入射到镜面上后等效形成一个虚光源,实光源与虚光源是一对相干光源
- 洛埃镜下的干涉可用杨氏双缝干涉类比,两个光源之间的距离等价为狭缝距离,光源到接受屏幕的垂直距离就是D
- 需要注意的是,入射光经过洛埃镜发射后会产生相位突变,发生半波损失,因此,光程差中除了包含两光源自身的光程差以外,还需要添加半个波长
空间相干性
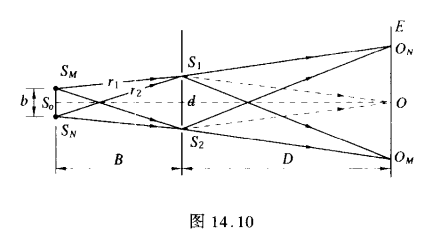
当我们把杨氏实验中的点光源换成线光源后,这里的线光源彼此之间是不相干的,在经过狭缝后会各自产生一套干涉条纹,频幕上的每一处都是各个干涉图样的叠加
上图中OM,ON分别是线光源的顶端和底端点光源经过狭缝干涉后的中央亮纹,在线光源宽度b不是很大的情况下,二者大致重合与中央对称点Q,但当距离逐渐增大时,二者将逐渐分离,这将使得屏幕图样的反衬度降低.
当线光源的宽度加宽到两端端点点光源经过狭缝后各自分别干涉形成的一级暗条纹正好落在中央对称点O时,干涉图样已经完全不能分辨,屏幕上总光强均匀分布,此时的线光源宽度就是空间干涉极限
当线光源宽度b达到空间干涉极限时,有
- $$\begin{aligned}
r_2-r_1=\frac{\lambda}{2}
\end{aligned}$$ - $$\begin{aligned}
r^2_2=B^2+(\frac{d+b}{2})^2
\end{aligned}$$ - $$\begin{aligned}
r^2_1=B^2+(\frac{d-b}{2})^2
\end{aligned}$$ - $$\begin{aligned}
r_2-r_1≈\frac{db}{2B}=\frac{\lambda}{2}
\end{aligned}$$ - $$\begin{aligned}
b=\frac{B\lambda}{d}
\end{aligned}$$
- $$\begin{aligned}
因此我们得到了空间相干的极限线宽度b,这表明只有当线光源的宽度小于该极限宽度时才能够获得相干光,换言之,只有当同一波阵面上的两点距离小于该极限宽度时,从这两点发出的次波才是相干的,这一性质称为空间相干性
薄膜干涉
等厚干涉
干涉图样中同一干涉级次条纹对应于薄膜上厚度相同点的连线,这样的干涉条纹称为等厚干涉条纹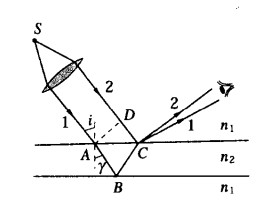
等厚干涉中的光程差可以表示为
$$\begin{aligned}
\delta = n_2(AB+BC)-n_1DC+\frac{\lambda}{2}
\end{aligned}$$
$$\begin{aligned}
\delta=2n_2 d\cos\gamma+\frac{\lambda}{2}
\end{aligned}$$
半波长加载项是因为不论折射率大小情况如何,必定会存在半波损失,因此光程差中需要添加半个波长- 劈尖干涉
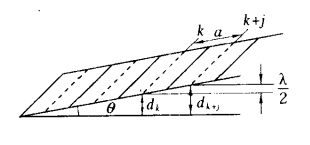
两条相邻的明条纹或暗条纹对应的空气层厚度都相等,两条相邻的明条纹或暗条纹之间的距离为a
$$\begin{aligned}
d_{k+1}-d_{k}=\frac{\lambda}{2}
\end{aligned}$$
$$\begin{aligned}
a\sin\theta=\frac{\lambda}{2}
\end{aligned}$$
因此可见劈尖的角度越小,干涉条纹间距越稀疏,越容易分辨,且最开始的条纹是暗纹 - 牛顿环
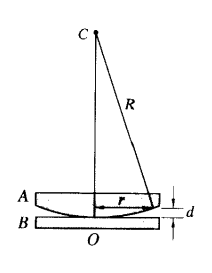
半径为r的环形条纹下对应的空气层d,由图可知
$$\begin{aligned}
R^2=r^2+(R-d)^2
\end{aligned}$$
$$\begin{aligned}
d=\frac{r^2}{2R}
\end{aligned}$$
$$\begin{aligned}
\delta = 2d+\frac{\lambda}{2}
\end{aligned}$$
由此,牛顿环的中央显然是暗纹
- 劈尖干涉
等倾干涉
干涉图样中同一干涉条纹是来自膜面的等倾角光线经过透镜聚焦后的轨迹,故称为等倾干涉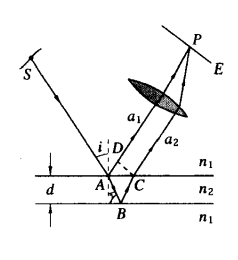
$$\begin{aligned}
\delta=2n_2d\cos\gamma+\frac{\lambda}{2}
\end{aligned}$$
迈克耳孙干涉仪
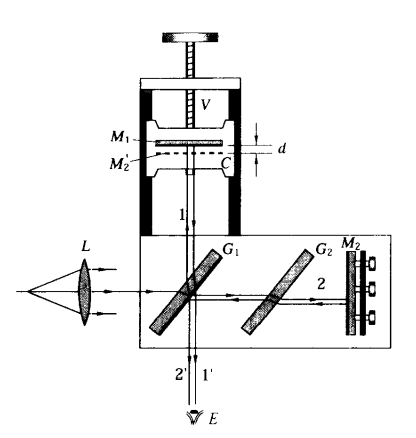
- 对于观察者来说,光线从M1,M2上的反射相当于来自距离为d的M1,M2’上的反射,其中M2’是平面镜M2经过G1半反半透膜反射所形成的虚像
- 显然这是光束的光程差只取决于厚度d,每移动半个波长时,视场就会出现一个级次亮条纹或暗条纹的变化,当从视场中第K次最亮到出现第K+N次最亮时,反射镜M1移动的距离$d=N\frac{\lambda}{2}$
- 时间相干性
实际光源的发光是独立的,随机的,间歇性的,一切实际光源发射的光是一个个的波列,当接连发出的前后两个波列完全没有重叠时,干涉就不可能发生.两光路之间的光程差超过波列长度L就不会再发生干涉,我们称这波列长度为光源所发射光的相干长度
光的衍射
惠更斯-菲涅尔原理
- 光的衍射现象
当一束光照射到小孔、细缝等尺寸接近光波长的微小障碍物时,光会绕过障碍物并偏离直线传播,在远处屏幕上就会观察到屏幕上出现明暗相间的条纹,称为光的衍射现象. - 光衍射现象的分类
- 菲涅尔衍射
菲涅尔衍射是近场衍射,其光源和接受屏到衍射屏的距离有限,或者光源无限远但接受屏到衍射屏距离有限 - 夫琅禾费衍射
夫琅禾费衍射是远场衍射,其光源和接受屏到衍射屏的距离均无限远,这意味这夫琅禾费衍射中的入射光和衍射光均为平行光
- 菲涅尔衍射
- 惠更斯原理
波面上任一点都可以看做次波源,发出球面次波,它们的包络面为下一时刻新的波阵面 - 惠更斯-菲涅尔原理
- 从同一波阵面上各点发出的次波是相干波
- 经过传播,在空间某点相遇时的叠加是相干叠加
- 菲涅尔积分公式
$$\begin{equation}
E=\int_S F\cdot k(\phi)\cdot\frac{1}{r}\cos(\Omega t-\frac{2\pi r}{\lambda})\mathrm{dS}
\end{equation}$$- 式$(4)$中各个物理量的意义分别是
- F是比例系数
- $k(\phi)$是倾斜因子
- 式$(4)$中各个物理量的意义分别是
- 菲涅尔-基尔霍夫衍射积分公式
基尔霍夫经过严格的电磁理论证明了菲涅尔积分公式的基本正确性,只需要将波前修正为任意形状的封闭曲面即可,并确定了比例系数和倾斜因子表达式
$$\begin{equation}
E=\oint_S F\cdot k(\phi)\cdot\frac{1}{r}\cos(\Omega t-\frac{2\pi r}{\lambda})\mathrm{dS}
\end{equation}$$
$$\begin{equation}
F=-\frac{i}{\lambda}=\frac{e^{-i\frac{\pi}{2}}}{\lambda}
\end{equation}$$
$$\begin{equation}
k(\varphi)=\frac{1}{2}(\cos\theta+\cos\theta_0)
\end{equation}$$- $\theta_0$为面元法线与实际光源S到次波源Q连线间的夹角,$\theta$为面元法线与次波源Q到接受屏上一点P连线间的夹角
- 当波前为球面的情况下,$\theta_0=0$
单缝的夫琅禾费衍射
- 菲涅尔半波带法
- 半波带
将波面分割成一系列等宽度的窄条,使得相邻窄条对应点发出的光线的光程差为半个波长,这样就形成了半波带 - 总宽度为a的狭缝,用一束平行单色光垂直狭缝入射,通过狭缝的光会发生衍射,衍射角相同的平行光经过透镜的汇聚作用将聚焦于一点.狭缝间可以分割出的半波带数目为
$$\begin{equation}
N=\frac{a\sin\varphi}{\frac{\lambda}{2}}
\end{equation}$$ - 当划分的半波带数目N是奇数时,衍射条纹为亮条纹;当划分的半波带数目N是偶数时,衍射条纹为暗条纹.这是因为两个相邻的相干光之间光程差为半个波长,处于干涉相消状态,因此当划分数目为奇数个时,就会有一条光线无从抵消,因而出现亮条纹
$$\begin{cases}
a\sin\varphi & = 2k\frac{\lambda}{2} \qquad暗条纹\
a\sin\varphi & = (2k+1)\frac{\lambda}{2} \qquad亮条纹
\end{cases}$$ - 衍射光强分布
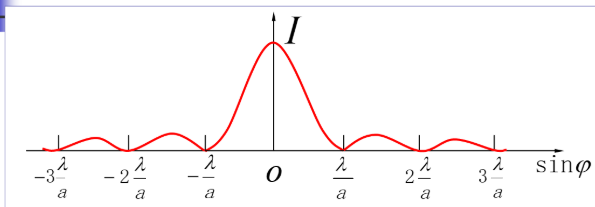
- 中央明纹宽度
中央明纹宽度定义为正负一级暗纹之间的距离 - 当衍射角增大时,衍射级次增加,但明纹光强会减小
- 中央明纹宽度
- 半波带
- 菲涅尔积分法
略 - 单缝衍射光强分布
$$\begin{equation}
I=I_m(\frac{\sin u}{u})^2 \quad u=\frac{\pi a\sin\theta}{\lambda}
\end{equation}$$- 极值点
光强分布的极值点满足
$$\begin{equation}
\frac{\mathrm{d}}{\mathrm{du}}(\frac{\sin u}{u})=0
\end{equation}$$
$$\begin{equation}
u=\tan u
\end{equation}$$ - 亮条纹角宽度
- 极值点
- 夫琅禾费矩孔衍射
衍射屏上开有a*b的矩孔,这样的矩孔可以看作是沿y方向的宽度为a的狭缝和沿x方向的宽度为b的狭缝的交集,衍射图样自然也是两个相互垂直的衍射花样的交集- 衍射光强分布
$$\begin{equation}
I=I_0(\frac{\sin u}{u})^2(\frac{\sin v}{v})^2
\end{equation}$$
$$\begin{equation}
u=\frac{\pi a\sin\theta_1}{\lambda} \quad v=\frac{\pi b\sin\theta_2}{\lambda}
\end{equation}$$ - $I_0$为入射光几何像点的衍射光强
- 衍射光强分布
- 夫琅禾费圆孔衍射
- 衍射光强分布
$$\begin{equation}
I=I_0[\frac{2J_1(x)}{x}]^2
\end{equation}$$ - $I_0$是屏幕中心光强,$J_1(x)$是一阶贝塞尔函数
- 衍射图样特点
- 同心圆环,明暗交错
- 中央为亮斑,其能量占据衍射光强总能量的84%,称为艾里斑
- 艾里斑的半角宽度为(D为衍射屏上的圆孔直径)
$$\begin{equation}
\Delta\theta_0=0.61\frac{\lambda}{R}=1.22\frac{\lambda}{D}
\end{equation}$$ - 艾里斑半径(f为透镜焦距)
$$\begin{equation}
\Delta r=1.22\frac{f\lambda}{D}
\end{equation}$$
- 衍射光强分布
光学仪器的分辨极限
- 瑞利判据
当一个像斑的中心刚好落在另一个像斑边缘时,认为两个像刚好能分辨,则此时两像斑中心的角距离刚好是艾里斑的半角宽度 - 望远镜的最小分辨角
$$\begin{equation}
\delta\phi=1.22\frac{\lambda}{D}
\end{equation}$$
最小分辨角越小,仪器的分辨本领越强.光学仪器的最小分辨角是由光的衍射效应决定的,是理论极限不可逾越
衍射光栅
狭缝宽度为a,狭缝间距为b,光栅常数d=a+b,衍射角为$\varphi$
光栅衍射是单缝衍射与缝间干涉综合作用的结果,缝间干涉决定干涉极大的位置(明纹位置),单缝衍射决定合成光的光强
光栅方程
相邻狭缝发出的光到达屏幕上同一点的光程差为
$$\begin{equation}
\delta = (a+b)\sin\varphi
\end{equation}$$
满足下式条件,则屏幕上出现明条纹,即干涉增强
$$\begin{equation}
(a+b)\sin\varphi=\pm k\lambda
\end{equation}$$主极大条纹
满足光栅方程的明条纹称为主极大明纹,其中k=0时的中央明条纹称为零级主极大,其外各级主极大对称分布在中央明条纹两侧谱线的缺级
- 缺级是指本应该出现主极大明条纹的位置却没有出现主极大明条纹
- 这是因为光栅衍射是单缝衍射和缝间干涉的综合作用,谱线缺级正是因为此时单缝衍射为暗纹
$$\begin{cases}
(a+b)\sin\varphi &=\pm k\lambda \quad 干涉明纹\
a\sin\varphi &=\pm k’\lambda \quad 衍射暗纹
\end{cases}$$
$$\begin{equation}
k=\frac{a+b}{b}k’
\end{equation}$$ - 满足$(22)$式就会出现谱线缺级
暗纹条件(缝间暗纹干涉,下面几个方程等价)
$$\begin{equation}
N(a+b)\sin\varphi\frac{2\pi}{\lambda}=\pm m\cdot 2\pi \quad (m不能整除N)
\end{equation}$$$$\begin{equation}
N(a+b)\sin\varphi=\pm m\lambda
\end{equation}$$$$\begin{equation}
(a+b)\sin\varphi=\pm(k+\frac{m}{N})\lambda
\end{equation}$$- 两个相邻主极大之间存在N-1个暗条纹
- 每两个暗纹之间存在一个光强很小的次级大,相邻两个主极大之间有N-2个次级大
- 次级大光强很小,两个主极大之间实际形成一片非常暗的背景
光栅主极大的半角宽
- 主极大两侧暗纹位置决定了主极大明条纹的宽度
- 主极大的半角宽度$\Delta\varphi$等于其最邻近的暗条纹与主极大亮纹间的夹角
$$\begin{equation}
\sin(\varphi_k+\Delta\varphi)-\sin\varphi_k=\frac{\lambda}{N(a+b)}
\end{equation}$$
$$\begin{equation}
\Delta\varphi=\frac{\lambda}{N(a+b)\cos\varphi_k}
\end{equation}$$
光栅衍射的光强分布
$$\begin{equation}
I=I_m(\frac{\sin\alpha}{\alpha})^2(\frac{\sin\frac{N\delta}{2}}{\frac{\delta}{2}})^2
\end{equation}$$
$$\begin{equation}
\delta=\frac{2\pi}{\lambda}(a+b)\sin\varphi \quad \alpha=\frac{\pi a\sin\varphi}{\lambda}
\end{equation}$$光栅的色散本领和色分辨本领
- 角色散本领
$$\begin{equation}
\mathrm{d}[(a+b)\sin\varphi]=\pm\mathrm{d\lambda}
\end{equation}$$
$$\begin{equation}
D_{\varphi}=\frac{\delta\varphi}{\delta\lambda}=\frac{k}{(a+b)\cos\varphi}
\end{equation}$$ - 线色散本领
$$\begin{equation}
D_l=fD_{\varphi}
\end{equation}$$ - 光栅的色散本领只反映主极大中心的分离程度
- 当角距离小于半角宽度时,不可分辨
- 当角距离等于半角宽度时,根据瑞利判据,刚好可以分辨
- 当角距离大于半角宽度时,可以分辨
- 角色散本领

This is an identification card as an honored membership of FeynmanDirac
Happy to see you follow FeynmanDirac, enjoy science together
 验证码启动中...
验证码启动中...
备用人机验证