矢量分析广泛应用于物理推导之中，为减少日后文章中的不必要说明和推导，特别制作一章矢量分析供读者参考学习.掌握矢量分析，是学习包括电磁场理论在内的物理学重要理论的必备数学手段，因此，矢量分析的掌握是不可或缺的，闲言少叙，我们开始矢量分析的冒险吧

矢量分析

矢量的乘积

• 数乘
  k为任意常数，则k$\vec{A}$ = $\vec{a}$(kA)，$\vec{a}$为单位矢量
• 标积
  $\vec{A}\cdot\vec{B} = \vert\vec{A}\vert\vert\vec{B}\vert<\vec{A},\vec{B}> = \vert\vec{A}\vert\vert\vec{B}\vert\cos(\theta_{AB})$，满足交换律和分配律
• 矢积
  $\vec{A}\times\vec{B} = \vec{a}\vert\vec{A}\vert\vert\vec{B}\vert\sin(\theta_{AB})$，$\vec{a}$是右手系下A转向B拇指所指向方向的单位矢量
  $\vec{A}\times\vec{B}$ = -$\vec{B}\times\vec{A}$，满足分配律但不满足交换律
• $\color{lime}{三矢量积}$
  $\vec{A}\cdot(\vec{B}\times\vec{C})$ = $\vec{B}\cdot(\vec{C}\times\vec{A}) + \vec{C}\cdot(\vec{A}\times\vec{B})$ $\Rightarrow$ “循环互换”
  $\vec{A}\times(\vec{B}\times\vec{C})$ = $\vec{B}(\vec{A}\cdot\vec{C})$ - $\vec{C}(\vec{A}\cdot\vec{B})$ $\Rightarrow$ “back-cab”

场

• 空间区域$\Omega$上每点对应某个物理量的一个标量或矢量，则此空间确定了这个物理量的场
• 若场中每一点的量既与位置有关又与时间有关，这种场就称为时变场，与时间无关的称为静态场
• 除了标量和矢量，既有大小又有张向的量称为二阶张量，简称张量或并矢.张量通常用双向箭头符号表示，$\overleftrightarrow{A}$，本文中为了方便(偷懒)，使用latex自带的张量表示法$\mathcal{A}$表示(虽然歪歪扭扭的但是，好打出来!)

矢量场的通量、散度和散度定理

• $\color{yellow}{通量}$
  面元$\mathrm{d}\vec{s}$位于矢量场$\vec{A}$中，定义$\vec{A}\cdot\mathrm{d}\vec{s}$为穿过面元的通量，记为$\mathrm{d}\phi$，那么
  $$\begin{aligned}
  \phi = \int_s\vec{A}\cdot\vec{a}\mathrm{d}s，\vec{a}是面元的外法向方向
  \end{aligned}$$
• $\color{yellow}{散度}$
  定义矢量$\vec{A}$在一点的散度为：
  $$\begin{aligned}
  \mathrm{div}\vec{A} = \lim_{\Delta V\to 0}\frac{\oint\vec{A}\cdot\mathrm{d}\vec{s}}{\Delta V}，
  \end{aligned}$$
  数学上可以证明
  $$\begin{aligned}
  \oint_s\vec{A}\mathrm{d}\vec{s} = (\frac{\partial A_x}{\partial x}+\frac{\partial A_y}{\partial y}+\frac{\partial A_z}{\partial z})\Delta V
  \end{aligned}$$
  定义
  $$\begin{aligned}
  \mathrm{div}\vec{A} = (\frac{\partial A_x}{\partial x}+\frac{\partial A_y}{\partial y}+\frac{\partial A_z}{\partial z}) = \nabla\cdot\vec{A}，\nabla 是哈密顿算子
  \end{aligned}$$
  若$\nabla\cdot\vec{A} = 0$，则称向量场$\vec{A}$为无散场，也称为无源场
• $\color{yellow}{散度运算基本公式}$
  $$\begin{aligned}
  \nabla\cdot(\vec{A}\pm\vec{B}) = \nabla\cdot\vec{A}\pm\nabla\cdot\vec{B}
  \
  \color{cyan}{\nabla\cdot(\phi\vec{A}) = \phi\nabla\cdot\vec{A} + \vec{A}\nabla\phi}
  \
  \color{cyan}{\nabla\cdot(\nabla\phi)} = \nabla^2\phi = \sum_{i=x,y,z}\frac{\partial^2 \phi}{\partial i^2}
  \ \nabla^2是Laplace算子
  \end{aligned}$$
• $\color{yellow}{散度定理}$
  $$\begin{aligned}
  \mathrm{div}\vec{A} = \lim_{\Delta V\to 0}\frac{\oint_s\vec{A}\cdot\mathrm{d}\vec{s}}{\Delta V} = \nabla\cdot\vec{A}\Rightarrow \int_V \nabla\cdot\vec{A}\mathrm{d}V = \oint_s\vec{A}\cdot\mathrm{d}\vec{s}
  \end{aligned}$$
  散度定理也被称为奥高公式
• $\color{yellow}{梯度积分公式}$
  设$\vec{C}$为任意常矢量，如同上面一样$\phi$为标量
  $$\begin{aligned}
  \nabla\cdot(\vec{C}\phi) = \vec{C}\nabla\cdot\phi + \phi\nabla\cdot\vec{C} \Rightarrow
  \int\nabla\cdot(\vec{C}\phi)\mathrm{d}V = \int\vec{C}\nabla\phi\mathrm{d}V + \int\phi\nabla\cdot\vec{C}\mathrm{d}V
  \end{aligned}$$
  因为$\vec{C}$为任意常矢量
  $$\begin{aligned}
  \int\nabla\cdot(\vec{C}\phi)\mathrm{d}V = \vec{C}\int\nabla\phi\mathrm{d}V = \oint\vec{C}\phi\mathrm{d}s
  \
  \Rightarrow \int\nabla\phi\mathrm{d}V = \oint\phi\mathrm{d}s
  \end{aligned}$$
  因此梯度积分公式为$\color{cyan}{\int\nabla\phi\mathrm{d}V = \oint\phi\mathrm{d}s }$

矢量场的环量、旋度和斯托克斯定理

• $\color{yellow}{环量}$
  矢量$\vec{A}$沿一封闭曲线的线积分定义为矢量$\vec{A}$沿该封闭曲线的环量，记为$\Gamma$
  $$\begin{aligned}
  \color{cyan}{\Gamma = \oint\vec{A}\cdot\mathrm{d}\vec{l}}
  \end{aligned}$$
• $\color{yellow}{旋度}$
  定义
  $$\begin{aligned}\mathrm{rot}\vec{A} = \vec{a}\lim_{\Delta S\to 0}[\frac{\oint\vec{A}\cdot\mathrm{d}\vec{l}}{\Delta S}]_{max}\end{aligned}$$
  表示在给定点处的最大环量面密度，用以表征某点处的漩涡源强度
  若$\mathrm{rot}\vec{A} = 0$，则称矢量场$\vec{A}$为无旋场或保守场
  旋度公式为
  [

  \mathrm{rot}\vec{A} = \left|\begin{array}{}
   \vec{a_x} &  \vec{a_y} & \vec{a_z} \\
   \frac{\partial }{\partial x} &   \frac{\partial }{\partial y} &  \frac{\partial }{\partial z} \\
   \vec{A_X} &  \vec{A_y} & \vec{A_z}  
  \end{array}\right|
  

  ]
  (为防止上式被数学引擎渲染失败，特此附上一张图)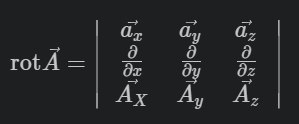
  
  或简单记为
  $$\begin{aligned}
  \mathrm{rot}\vec{A} = \nabla\times\vec{A}
  \end{aligned}$$
• $\color{yellow}{旋度基本公式}$
  $$\begin{aligned}
  \nabla\times(\vec{A}\pm\vec{B}) = \nabla\times\vec{A}\pm\nabla\times\vec{B} \
  \color{cyan}{\nabla\times(\phi\vec{A}) = \phi\nabla\times\vec{A} + \nabla\phi\times\vec{A}} \
  \color{cyan}{\nabla\cdot(\vec{A}\times\vec{B}) = \vec{B}\cdot(\nabla\times\vec{A}) - \vec{A}\cdot(\nabla\times\vec{B})} \
  \color{cyan}{\nabla\times\nabla\times\vec{A} = \nabla(\nabla\cdot\vec{A}) - \nabla^2\vec{A}}
  \end{aligned}$$
  小提一下，后两个公式与最前面介绍的三矢量公式的记忆是一致的哦
• $\color{yellow}{斯托克斯公式}$
  $$\begin{aligned}
  \mathrm{rot}\vec{A} = \vec{a}\lim_{\Delta S\to 0}[\frac{\oint\vec{A}\mathrm{d}l}{\Delta S}]_{max} = \nabla\times\vec{A} \
  \Rightarrow \int(\nabla\times\vec{A})\mathrm{d}s = \oint\vec{A}\cdot\mathrm{d}\vec{l}
  \end{aligned}$$
• $\color{yellow}{旋度定理}$
  $$\begin{aligned}\int_V(\nabla\times\vec{A})\mathrm{d}V = -\oint_S\vec{A}\times\mathrm{d}\vec{S}\end{aligned}$$
  小提一下，证明是简易的，拆分体积元并运用斯托克斯公式即可，只是需要注意的是各个微元的实际意义以避免混淆.

标量场、矢量场的性质定理

• $\color{red}{梯度场的旋度恒为零}$
  $$\begin{aligned}
  \color{yellow}{\nabla\times\nabla\phi \equiv 0}
  \end{aligned}$$
  证明：
  $$\begin{equation}
  \int(\nabla\times\nabla\phi)\cdot\mathrm{d}\vec{S} = \oint \nabla\phi\cdot\mathrm{d}\vec{l}
  \end{equation}$$
  $$\begin{equation}
  \nabla\phi = i\frac{\partial \phi}{\partial x}+j\frac{\partial \phi}{\partial y}+k\frac{\partial \phi}{\partial z}
  \end{equation}$$
  $$\begin{equation}
  \mathrm{d}\vec{l} =(i\cos\alpha + j\cos\beta + k\cos\gamma)\mathrm{d}l
  \end{equation}$$
  由(2)、(3)
  $$\begin{aligned}\nabla\phi\cdot\mathrm{d}\vec{l} = \sum_{i=x,y,z}\frac{\partial \phi}{\partial i}\mathrm{d}i = \mathrm{d}\phi\end{aligned}$$
  于是(1)中右侧的环积分结果为零，得证
• $\color{red}{旋度场的散度恒为零}$
  $$\begin{aligned}
  \color{yellow}{\nabla\cdot(\nabla\times\vec{A}) \equiv 0}
  \end{aligned}$$
  证明：
  $$\begin{equation}
  \int(\nabla\cdot(\nabla\times\vec{A}))\cdot\mathrm{d}\vec{V} = \oint_S(\nabla\times\vec{A})\cdot\mathrm{d}\vec{S}
  \end{equation}$$
  $$\begin{equation}
  \oint(\nabla\times\vec{A})\cdot\mathrm{d}\vec{S} = \int(\nabla\times\vec{A})\cdot\vec{e_1}\mathrm{d}S + \int(\nabla\times\vec{A})\cdot\vec{e_2}\mathrm{d}S = \oint_{l_1}\vec{A}\cdot\mathrm{d}\vec{l} + \oint_{l_2}\vec{A}\cdot\mathrm{d}\vec{l}
  \end{equation}$$
  根据斯托克斯公式的方向定义可知而两封闭曲线的绕行方向是相反的，即
  $$\begin{equation}
  \oint_{l_1}\vec{A}\cdot\mathrm{d}\vec{l} + \oint_{l_2}\vec{A}\cdot\mathrm{d}\vec{l} = 0
  \end{equation}$$
  于是得证
• $\color{yellow}{上面两个定理表明无散场可以表示为一个旋度场，无旋场可以表示为一个梯度场，这句话十分重要奥}$
  $$
  \begin{cases}
  \nabla\cdot f = 0 \Rightarrow f = \nabla\times\vec{A} \
  \nabla\times\vec{f} = 0 \Rightarrow \vec{f} = \nabla\cdot\vec{A}
  \end{cases}
  $$
• $\color{yellow}{散度和旋度均为零的场称为调和场，调和场满足Laplace方程}$
  $$\begin{aligned}
  \nabla\times\vec{f} = 0 \Rightarrow \vec{f} = \nabla\cdot\phi \ \Rightarrow
  0 = \nabla\cdot(\nabla\cdot\phi) = \nabla^2\phi
  \end{aligned}$$
  满足$\nabla^2\phi = 0$的函数$\phi$称为调和函数该式称为Laplace方程.
  调和场只存在于有限空间中，无限空间中不存在调和场

三大定理

• $\color{yellow}{标量格林定理}$
  将矢量$\vec{A}$表示为标量函数$\phi$和另一标量函数$\psi$梯度的乘积
  $$\begin{aligned}
  \nabla\cdot\vec{A} = \nabla\cdot(\phi\nabla\psi) = \phi\nabla^2\psi + \nabla\phi\nabla\psi
  \end{aligned}$$
  应用散度定理
  $$\begin{aligned}
  \int_V\nabla\cdot\vec{A}\mathrm{d}V = \int_V(\phi\nabla^2\psi + \nabla\phi\nabla\psi)\mathrm{d}V = \oint_S(\phi\nabla\psi)\cdot\vec{a}\mathrm{d}S = \oint\phi\frac{\partial \psi}{\partial n}\mathrm{d}S
  \end{aligned}$$
  上式称为格林第一定理
  交换$\phi、\psi$的位置并相减可得到
  $$\begin{aligned}
  \int_V(\phi\nabla^2\psi - \psi\nabla^2\phi)\mathrm{d}V = \oint(\phi\frac{\partial \psi}{\partial n} - \psi\frac{\partial \phi}{\partial n})\mathrm{d}S
  \end{aligned}$$
  上式称为格林第二定理
• $\color{yellow}{矢量场的唯一性定理}$
  矢量场的唯一性定理表述为一个矢量场可以被其散度、旋度和区域边界上的边界条件所唯一确定
• $\color{yellow}{亥姆霍兹定理}$
  亥姆霍兹定理表述为若矢量场$\vec{f}$在给定的无限空间内处处单值，且导数连续有界，而源分布在有限区域中，则矢量场$\vec{f}$可分解为无旋场和无散场之和.