Atomic physics Ⅰ
请注意,本文最近一次更新于:2022-01-09,文章内容可能已经不具有时效性,请谨慎参考
本文最后更新于:2022年1月9日星期日上午10点36分 +08:00
原子物理学与量子力学导论来啦!
本文是第Ⅰ部分,是从经典到量子的过渡❤
原子的位型:卢瑟福模型
库伦散射公式
库伦散射公式的推导
参数诠释
下面列出公式中的参数及其意义- $v_i$,$v_f$:表征散射前后的初末速度
- b:瞄准距离
- $\theta$:散射偏转角
- m,m’:分别表征入射粒子和靶核质量
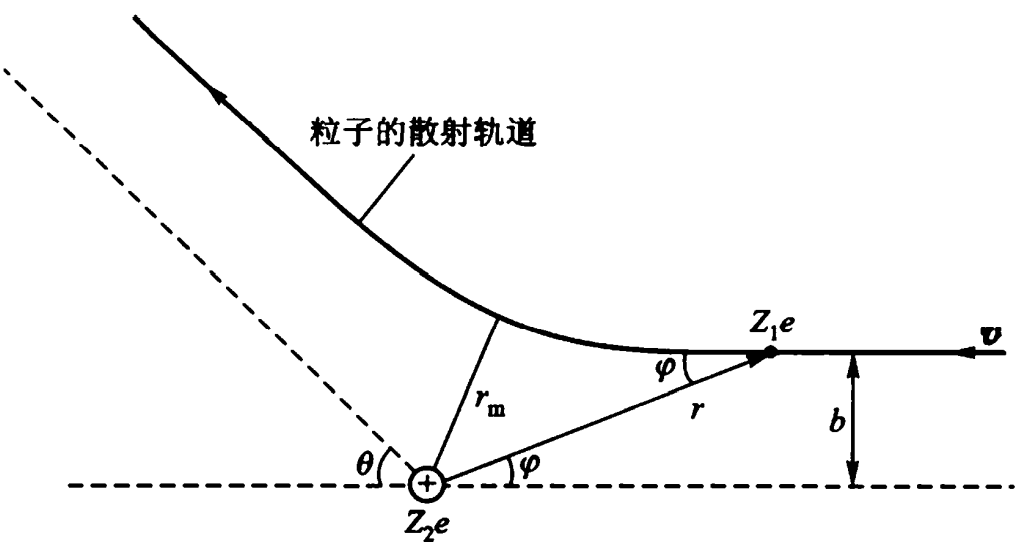
在推导库伦散射公式时,我们做出如下假定
- 只发生单次散射
- 只存在库伦相互作用
- 核外电子的作用可以忽略
- 靶核是静止的
下面开始正式推导
- 根据牛顿动力学给出动力学方程
$$\begin{aligned}
\frac{Z_1Z_2e^2}{4\pi\varepsilon_0r^2}\vec{e_r}=m\frac{\mathrm{d\vec{v}}}{\mathrm{dt}}
\end{aligned}\tag{1}$$ - 库仑力是有心力,有心力场中角动量守恒
$$\begin{aligned}
L=mr^2\frac{\mathrm{d\varphi}}{\mathrm{dt}}=mvb
\end{aligned}\tag{2}$$ - 由$(1),(2)$可以得到下述公式
$$\begin{aligned}
\mathrm{d\vec{v}}=\frac{Z_1Z_2e^2}{4\pi\varepsilon_0L}\mathrm{d\varphi}\vec{e_r}
\end{aligned}\tag{3}$$ - 左侧积分得到
$$\begin{aligned}
\int\mathrm{d\vec{v}}=|\vec{v_f}-\vec{v_i}|\vec{e_u}
\end{aligned}\tag{4}$$
式中$\vec{e_u}$是速度变化量方向的单位矢量 - 根据能量守恒定律,由于我们假定碰撞前后靶核始终不动,因此显然有下式成立
$$\begin{aligned}
E=\frac{1}{2}m|\vec{v_i}|^2=\frac{1}{2}m|\vec{v_f}|^2
\end{aligned}\tag{5}$$
上式表明碰撞前后速度的数值必然相等,记为$\vec{v}$,只是存在方向上的不同.通过矢量图示分析可知,速度矢量的变化量$\vec{v}_f-\vec{v}_i$的大小是$|\vec{v}_f-\vec{v}_i|=2\vec{v}\sin\frac{\theta}{2}$ - 积分式右侧是对径矢$\vec{r}$的方向积分,其结果为
$$\begin{aligned}
\int\vec{e}_r\mathrm{d\varphi}&=\int_{0}^{\pi-\theta}(\vec{i}\cos\varphi+\vec{j}\sin\varphi)\mathrm{d\varphi} \\
&=2\cos\frac{\theta}{2}(\vec{i}\sin\frac{\theta}{2}+\vec{j}\cos\frac{\theta}{2})
\end{aligned}\tag{6}$$
其中径矢矢量由坐标轴基矢量合成 - 将式$(4)$,$(5)$,$(6)$的结果统筹可以得到
$$\begin{aligned}
v\sin\frac{\theta}{2}&=\frac{1}{4\pi\varepsilon_0}\frac{Z_1Z_2e^2}{L}\cos\frac{\theta}{2} \\
&=\frac{1}{4\pi\varepsilon_0}\frac{Z_1Z_2e^2}{mvb}\cos\frac{\theta}{2}
\end{aligned}\tag{7}$$ - 于是我们得到库伦散射公式
$$\begin{aligned}
b=\frac{a}{2}\cot\frac{\theta}{2}
\end{aligned}\tag{8}$$
其中
$$\begin{aligned}
a\equiv\frac{1}{4\pi\varepsilon_0}\frac{Z_1Z_2e^2}{E}
\end{aligned}\tag{9}$$小结
库伦散射公式:
$$\begin{aligned}
b=\frac{a}{2}\cot\frac{\theta}{2}
\end{aligned}\tag{8}$$
$$\begin{aligned}
a\equiv\frac{1}{4\pi\varepsilon_0}\frac{Z_1Z_2e^2}{E}
\end{aligned}\tag{9}$$
- 根据牛顿动力学给出动力学方程
- 库伦散射公式的修正
我们之前的假定靶核不动在实验中往往是不可能做到的,因此,我们将其视为两体问题处理,这就需要修正到质心系中处理,下面我们对所做出的修正进行说明.- 修正说明
- $\theta\rightarrow\theta_c$ 即将原点放置在两体系统的质心位置
- $E\rightarrow E_c$ 即将动能修正为质心动能
- $m\rightarrow m_c$ 即将质量修正为约化质量
$$\begin{aligned}
E_c=\frac{1}{2}m_cv^2
\end{aligned}$$
$$\begin{aligned}
m_c=\frac{mm’}{m+m’}
\end{aligned}$$
$$\begin{aligned}
E_c=\frac{m’}{m+m’}E \quad E=\frac{1}{2}mv^2
\end{aligned}$$
- 根据上述修正可以看出,当靶核质量远大于入射粒子质量时,质心动能近似等于实验室系动能,因此当满足靶核质量远远大于入射粒子质量时,上述修正可以忽略不计
卢瑟福散射公式
- 修正说明
- 卢瑟福公式的推导
从库伦公式中可以看出,只要瞄准距离大,散射角就小,对于某一确定的瞄准距离,其散射角是确定的
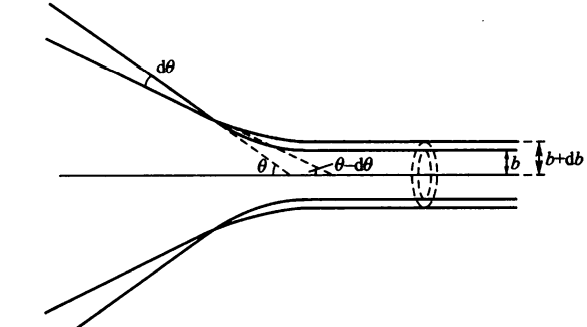
我们取微元分析.对于那些瞄准距离在b到b+db之间的粒子,经过散射必然定向$\theta$到$\theta-\mathrm{d\theta}$之间的空心圆锥体射出,如上图所示.
设一铝箔的面积为A,厚度为t,则粒子打在这个环上的概率显然为(显然是均匀分布)
$$\begin{aligned}
\frac{2\pi b|\mathrm{db}|}{A}
\end{aligned}\tag{10}$$
瞄准距离b的微分结果为
$$\begin{aligned}
\mathrm{db}=\frac{a}{2}\mathrm{d}(\cot\frac{\theta}{2})=-\frac{a}{4}\csc^2\frac{\theta}{2}\mathrm{d\theta}
\end{aligned}\tag{11}$$
将式$(11)$代入$(10)$可得
$$\begin{aligned}
\frac{2\pi b|\mathrm{db}|}{A}=\frac{a^2 2\pi\sin\theta\mathrm{d\theta}}{16A\sin^4\frac{\theta}{2}}
\end{aligned}\tag{12}$$
射出角度范围构成的空心圆锥体张成的立体角为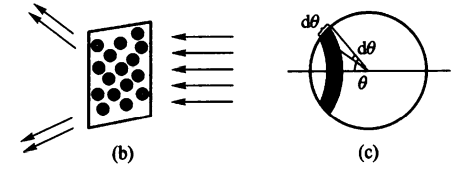
$$\begin{aligned}
\mathrm{d\Omega}=\frac{\mathrm{dS}}{r^2}
\end{aligned}\tag{13}$$
空心圆锥体立体角对应的面积是一个圆壳
$$\begin{aligned}
\mathrm{dS}=2\pi r\sin\theta r\mathrm{d\theta}
\end{aligned}\tag{14}$$
由此得到立体角为
$$\begin{aligned}
\mathrm{d\Omega}=2\pi\sin\theta\mathrm{d\theta}
\end{aligned}\tag{15}$$
将$(15)$式结果代入$(12)$可得
$$\begin{aligned}
\frac{2\pi b|\mathrm{db}|}{A}=\frac{a^2\mathrm{d\Omega}}{16A\sin^4\frac{\theta}{2}}
\end{aligned}\tag{16}$$由上图(b)所示,一个薄箔有许多这样的环:对应于一个原子核就存在一个环;假如在单位体积内的原子核数为n则在体积At内共存在nAt个原子核,因而也会有nAt个环.每个粒子搭载这样的换上的散射角都是$\theta$,故这样一个粒子被散射在立体角范围内的概率为
$$\begin{aligned}
\mathrm{dp(\theta)}=\frac{a^2\mathrm{d\Omega}}{16A\sin^4\frac{\theta}{2}}nAt
\end{aligned}\tag{17}$$上式是一个粒子的立体角方向概率分布,当有N个粒子时,在立体角方向上测算到的粒子数应为
$$\begin{aligned}
\mathrm{dN’}=N\frac{a^2\mathrm{d\Omega}}{16A\sin^4\frac{\theta}{2}}nAt
\end{aligned}\tag{18}$$定义微分截面
$$\begin{aligned}
\sigma_c(\theta)\equiv\frac{\mathrm{d}\sigma(\theta)}{\mathrm{d}\Omega}\equiv\frac{\mathrm{dN’}}{Nnt\mathrm{d}\Omega}
\end{aligned}\tag{19}$$卢瑟福公式
$$\begin{aligned}
\sigma_c(\theta)=\frac{a^2}{16\sin^4\frac{\theta}{2}}=(\frac{1}{4\pi\varepsilon_0}\frac{Z_1Z_2e^2}{4E})^2\frac{1}{\sin^4\frac{\theta}{2}}
\end{aligned}\tag{20}$$小结
卢瑟福公式:
$$\begin{aligned}
\sigma_c(\theta)=(\frac{1}{4\pi\varepsilon_0}\frac{Z_1Z_2e^2}{4E})^2\frac{1}{\sin^4\frac{\theta}{2}}
\end{aligned}$$
对于同一种粒子源和散射体,$\mathrm{dN’}\sin^4\frac{\theta}{2}=const$
对于同一粒子源和同一散射体材料,在同一散射角,$\mathrm{dN’}\propto t$
对于同一散射体和同一散射角,$\mathrm{dN’}E^2=const$
对于同一粒子源,同一散射角和同一nt值,$\mathrm{dN’}\propto Z^2$
原子的量子态:玻尔模型
玻尔的氢原子理论
玻尔的氢原子理论概述
定态假设
绕核运动的电子作圆周运动,但只能在一些特定的分立轨道上运动。在这些轨道上运动的电子绕核圆周运动时不发生电磁辐射,这就是定态假设,也称为定态条件
原子只能长时间的处于一些稳定的状态,即定态,各个定态有确定的能量,他们之间的能量数值是分立的,称为量子化能级或能量的量子化能级跃迁假设
正常情况下,核外电子处于稳定的定态轨道上,不会产生电磁辐射,但是当核外电子受到外界因素的影响时,可能从一个定态能级跃迁到另一个定态能级。在能级之间出现跃迁时,辐射出光子的频率是确定的
$$\begin{aligned}
\mathrm{h\nu}=E_2-E_1
\end{aligned}\tag{21}$$
这即为玻尔的能级跃迁假设,又称频率条件角动量量子化假设
为了确定氢原子能级和光谱频率,玻尔提出了角动量量子化假设
$$\begin{aligned}
L=m_evr_n=n\mathrm{\hbar} \quad n=1,2,3\cdots
\end{aligned}\tag{22}$$
$$\begin{aligned}
\mathrm{\hbar}=\frac{\mathrm{h}}{2\pi}
\end{aligned}$$氢原子的轨道半径方程
核外电子绕核运动的动力学方程为
$$\begin{aligned}
\frac{m_ev^2}{r}=\frac{Ze^2}{4\pi\varepsilon_0r^2}
\end{aligned}\tag{23}$$
代入$(22)$得
$$\begin{aligned}
r_n=\frac{4\pi\varepsilon_0\mathrm{\hbar^2}}{m_eZe^2}n^2
\end{aligned}\tag{24}$$氢原子的轨道能量表达式
取无穷远处为势能参考零点,于是容易得到总能量方程
$$\begin{aligned}
E=E_k+E_p=-\frac{Ze^2}{8\pi\varepsilon_0r}
\end{aligned}\tag{25}$$
代入$(24)$得
$$\begin{aligned}
E=-\frac{Z^2m_ee^4}{(4\pi\varepsilon_0)^2\cdot 2\mathrm{\hbar^2}n^2}=-Z^2\frac{Rhc}{n^2}
\end{aligned}\tag{26}$$
里德伯场量的表达式为
$$\begin{aligned}
R=\frac{2\pi^2e^4m_e}{(4\pi\varepsilon_0)^2ch^3}=109737.315cm^{-1}
\end{aligned}\tag{27}$$
小结
原子轨道半径表征式
$$\begin{aligned}
r_n=\frac{4\pi\varepsilon_0\mathrm{\hbar^2}}{m_eZe^2}n^2
\end{aligned}$$
原子轨道能量表征式
$$\begin{aligned}
E=-\frac{Z^2m_ee^4}{(4\pi\varepsilon_0)^2\cdot 2\mathrm{\hbar^2}n^2}=-Z^2\frac{Rhc}{n^2}
\end{aligned}$$
对应原理
对应原理用于揭示宏观范围与微观范围内不同理论之间的过渡关系
- 对应原理
在围观范围内的现象与宏观范围的现象可以各自遵从本范围的规律,但当把围观范围内的定律扩展到宏观范围内的经典规律时,则他们得到的数值结果应当一致
下面我们由对应原理导出角动量量子化假设的结果
对于氢原子,其两个不同能级之间跃迁产生的光谱频率可以写成
$$\begin{aligned}
\nu=\tilde{\nu}c=Rc(\frac{1}{n^2}-\frac{1}{m^2})=Rc\frac{(n+m)(m-n)}{n^2m^2}
\end{aligned}$$
当n很大时,两个相邻能级之间的跃迁频率近似为
$$\begin{aligned}
\nu=\frac{2Rc}{n^3}
\end{aligned}$$
按照对应原理,它应该等于经典频率式
$$\begin{aligned}
f=\frac{v}{2\pi r}=\frac{e}{2\pi}\sqrt{\frac{Z}{4\pi\varepsilon_0 mr^3}}
\end{aligned}$$
由此可以得到r的表达式
$$\begin{aligned}
r=\sqrt[3]{\frac{1}{4\pi\varepsilon_0}\frac{e^2}{16\pi^2R^2c^2m_{e}}}n^2
\end{aligned}$$
将r代入经典能量表达式
$$\begin{aligned}
E=-\frac{Ze^2}{8\pi\varepsilon_0 r}
\end{aligned}$$
便可以得到里德伯常量
$$\begin{aligned}
R=\frac{2\pi^2e^4m_{e}}{(4\pi\varepsilon_0)^2ch^3}
\end{aligned}$$
将R带回经典半径表达式便可以得到量子化的氢原子轨道半径
$$\begin{aligned}
r_{n}=\frac{4\pi\varepsilon_0\hbar^2}{m_{e}e^2}n^2
\end{aligned}$$
代入经典力学的角动量定义式可得
$$\begin{aligned}
L=\sqrt{\frac{m_{e}e^2r}{4\pi\varepsilon_0}}
\end{aligned}$$
将量子化的氢原子半径代入上式便可以得到
$$\begin{aligned}
L=n\hbar
\end{aligned}$$
二体问题:修正项
与推理库伦散射公式时类似,我们假定核不动是不合理的,同样地,在玻尔的几个假设中我们假定核不动的结果也需要进行修正
- 设原子核的质量为$m_A$,电子的质量为$m_e$,有电子核中心核组成的二体系统的约化质量为
$$\begin{aligned}
\mu=\frac{m_Am_e}{m_A+m_e}
\end{aligned}\tag{28}$$
相应地,里德伯常量表达式修正为
$$\begin{aligned}
R_A=\frac{2\pi^2e^4\mu}{(4\pi\varepsilon_0)^2ch^3}=R\frac{1}{1+\frac{m_e}{m_A}}
\end{aligned}\tag{29}$$
轨道半径修正为
$$\begin{aligned}
r_n=\frac{4\pi\varepsilon_0\mathrm{\hbar^2}}{\mu Ze^2}n^2
\end{aligned}\tag{30}$$
轨道能量修正为
$$\begin{aligned}
E=-\frac{Z^2\mu e^4}{(4\pi\varepsilon_0)^2\cdot 2\mathrm{\hbar^2}n^2}=-Z^2\frac{R_Ahc}{n^2}
\end{aligned}\tag{31}$$
氢原子光谱线系
| 线系 | 经验公式 | n取值 |
|---|---|---|
| 莱曼系 | $\tilde{\nu}=R_H[\frac{1}{1^2}-\frac{1}{n^2}]$ | $2,3,4\cdots$ |
| 巴尔末系 | $\tilde{\nu}=R_H[\frac{1}{2^2}-\frac{1}{n^2}]$ | $3,4,5\cdots$ |
| 帕邢系 | $\tilde{\nu}=R_H[\frac{1}{3^2}-\frac{1}{n^2}]$ | $4,5,6\cdots$ |
| 布喇开系 | $\tilde{\nu}=R_H[\frac{1}{4^2}-\frac{1}{n^2}]$ | $5,6,7\cdots$ |
| 普丰德系 | $\tilde{\nu}=R_H[\frac{1}{5^2}-\frac{1}{n^2}]$ | $6,7,8\cdots$ |
- 里德伯方程
$$\begin{aligned}
\tilde{\nu}=\frac{1}{\lambda}=R_H[\frac{1}{n^2}-\frac{1}{m^2}]=T(n)-T(m) \quad m\ge n+1
\end{aligned}\tag{32}$$
类氢粒子
- 类氢离子是原子核外只有一个电子,而核电荷数大于1的体系
- 根据轨道能量表达式可知$E_n\propto Z^2$
相应的光谱公式为
$$\begin{aligned}
\tilde{\nu}=\frac{1}{\lambda}=Z^2R_A(\frac{1}{n^2}-\frac{1}{m^2})=R_A(\frac{1}{(\frac{n}{Z})^2}-\frac{1}{(\frac{m}{n})^2})
\end{aligned}\tag{33}$$ - 对于$He^{+}$离子,其Z=2,1897年天文学家毕克林发现了其发射的谱系,由此命名为毕克林系
毕克林线系的波数可用下式表达
$$\begin{aligned}
\tilde{\nu}=R(\frac{1}{2^2}-\frac{1}{k^2}) \quad k=2.5,3,3.5,\cdots
\end{aligned}$$
此后还相继发现了福勒系、第一和第二莱曼系
相应的谱线公式为
$$\begin{aligned}
\tilde{\nu}=4R(\frac{1}{3^2}-\frac{1}{n^2}) \quad n=4,5,6\cdots
\end{aligned}$$
$$\begin{aligned}
\tilde{\nu}=4R(\frac{1}{1^2}-\frac{1}{n^2}) \quad n=2,3,4,\cdots
\end{aligned}$$
$$\begin{aligned}
\tilde{\nu}=4R(\frac{1}{2^2}-\frac{1}{n^2}) \quad k=3,4,5,\cdots
\end{aligned}$$
玻尔模型的推广
由于玻尔模型除了三个假设之外,还默认简化核外电子的轨道为圆轨道且没有考虑电子运动的相对论效应,因此对于更为复杂的原子,玻尔模型需要进一步推广
电子椭圆轨道的量子化
在玻尔提出氢原子的轨道角动量量子化条件不久后,威尔逊、石原和索莫非分别独立地提出了普适的量子化条件
$$\begin{aligned}
\oint p\mathrm{dq}=nh
\end{aligned}\tag{34}$$
式中p,q分别为广义动量和广义坐标,此式称为量子化通则.若p为动量,则q为位移;若p为角动量,则q为角位移.
例如,如果描述的是电子的圆周运动,则角动量L应为常数
$$\begin{aligned}
L\oint\mathrm{d\phi}=nh \Rightarrow L=n\hbar
\end{aligned}$$
电子绕原子核运动的轨道不只是圆形轨道,因为按照行星运动模型,电子运动一般应是椭圆轨道.1916年索莫非提出椭圆轨道理论.采用极坐标描述电子的椭圆运动.根据动力学原理,我们知道在极坐标系下动量与角动量的表示分别为
$$\begin{aligned}
p_r=m\dot{r} \quad p_{\phi}=mr^2\dot{\phi}
\end{aligned}\tag{35}$$
因此原子核与核外电子组成的体系的总能量为
$$\begin{aligned}
E=E_k+E_p=\frac{1}{2}m(\dot{r}^2+r\dot{\phi}^2)-\frac{Ze^2}{4\pi\varepsilon_0 r}
\end{aligned}\tag{36}$$
对每一个广义量运用量子化通则可得
$$\begin{aligned}
\oint{p_r}\mathrm{dr}=n_rh
\end{aligned}\tag{37}$$
$$\begin{aligned}
\oint{p_{\phi}}\mathrm{d\phi}=n_{\phi}h
\end{aligned}\tag{38}$$
由于有心力场中角动量守恒,因此可得
$$\begin{aligned}
p_{\phi}=mr^2\dot{\phi}=n\hbar
\end{aligned}\tag{39}$$
将原子核置于椭圆的一个焦点处,并以此焦点为原点建立极坐标系,则椭圆的极坐标方程为1
$$\begin{aligned}
r=\frac{a(1-e^2)}{1+e\cos\phi} \quad e=\frac{c}{a},为椭圆的离心率
\end{aligned}$$
由式$(37)$,$(39)$可以导出电子作椭圆运动的半短轴与半长轴之比2
$$\begin{aligned}
\frac{b}{a}=\frac{n_{\phi}}{n_{\phi}+n_{r}}
\end{aligned}\tag{40}$$
分别考虑常州与椭圆的两个交点处的体系总能量情况,此时极角分别为0和$\pi$,在这两个点处的平均动能均为零
$$\begin{aligned}
E&=\frac{1}{2}mr^2\dot{\phi}-\frac{Ze^2}{4\pi\varepsilon_0 r}=\frac{p_{\phi}^2}{2mr^2}-\frac{Ze^2}{4\pi\varepsilon_0} \\
&=\frac{1}{2ma^2}\frac{1}{(1-e^2)}(n\hbar)^2-\frac{Ze^2}{4\pi\varepsilon_0 a}\frac{1}{1-e} \\
&=\frac{1}{2ma^2}[\frac{1+e}{1-e^2}]^2(n\hbar)^2-\frac{Ze^2}{4\pi\varepsilon_0 a}\frac{1+e}{1-e^2} \quad \phi=0
\end{aligned}\tag{41}$$
$$\begin{aligned}
E=\frac{1}{2ma^2}[\frac{1-e}{1-e^2}]^2(n\hbar)^2-\frac{Ze^2}{4\pi\varepsilon_0 a}\frac{1-e}{1-e^2} \quad \phi=\pi
\end{aligned}\tag{42}$$
以上两个式子对一切离心率e成立,若体系的能量守恒,则利用上面两式相等可以解出椭圆轨道的长轴和短轴
$$\begin{aligned}
a=n^2\frac{4\pi\varepsilon_0 \hbar^2}{Zme^2}=n^2\frac{z_1}{Z} \quad a_1=\frac{4\pi\varepsilon_0\hbar^2}{me^2}
\end{aligned}\tag{43}$$
$$\begin{aligned}
b=nn_{\phi}\frac{a_1}{Z}
\end{aligned}\tag{44}$$
$a_1$即为氢原子的第一玻尔半径
式中的n表示主量子数,从式中可以看出椭圆轨道的半长轴决定于n而与角量子数$n_{\phi}$无关,所以主量子数相同的轨道,其半长轴是相等的.角量子数不能为零,否则就不再是曲线运动;但是径量子数可以为零,例如当电子做圆周运动时不存在径向速度,故径量子数可以为零,因此有
$$\begin{aligned}
n_{\phi}=1,2,3,\cdots,n \\
n_{r}=n-1,n-2,\cdots,2,1,0
\end{aligned}$$
利用式$(40)$,$(43)$,$(44)$可以得出椭圆离心率与主量子数和角量子数的关系
$$\begin{aligned}
n_{\phi}^2=(1-e^2)n^2
\end{aligned}\tag{45}$$
椭圆轨道体系的能量为
$$\begin{aligned}
E_n=-\frac{Z^2m_{e}e^4}{(4\pi\varepsilon_0)^2 2\hbar^2n^2}=-Z^2\frac{Rhc}{n^2}
\end{aligned}\tag{46}$$
小结
量子化通则
$$\begin{aligned}
\oint p\mathrm{dq}=nh
\end{aligned}$$
电子作椭圆运动的半短轴与半长轴之比
$$\begin{aligned}
\frac{b}{a}=\frac{n_{\phi}}{n_{\phi}+n_{r}}
\end{aligned}$$
椭圆离心率与主量子数和角量子数的关系
$$\begin{aligned}
n_{\phi}^2=(1-e^2)n^2
\end{aligned}$$
椭圆轨道体系的能量为
$$\begin{aligned}
E_n=-\frac{Z^2m_{e}e^4}{(4\pi\varepsilon_0)^2 2\hbar^2n^2}=-Z^2\frac{Rhc}{n^2}
\end{aligned}$$
相对论效应的修正
根据狭义相对论有
$$\begin{aligned}m=\frac{m_0}{\sqrt{1-\beta^2}}\quad \beta=\frac{v}{c} \end{aligned}\tag{47}$$
$$\begin{aligned}
E_k=m_0c^2\big[ \frac{1}{\sqrt{1-\beta^2}}-1\big]
\end{aligned}\tag{48}$$下面按照狭义相对论改写类氢离子的能量公式
轨道半径修正
$$\begin{aligned}
r_n=\frac{4\pi\varepsilon_0\hbar^2n^2}{me^2Z}
\end{aligned}\tag{48}$$
势能修正
$$\begin{aligned}
E_p=\frac{Ze^2}{4\pi\varepsilon_0 r_n}=\frac{Z^2}{n^2}\cdot(\frac{e}{4\pi\varepsilon_0\hbar c})^2\cdot mc^2=\frac{Z^2}{n^2}\cdot\alpha^2\cdot mc^2
\end{aligned}\tag{49}$$
体系能量修正
$$\begin{aligned}
E_n=-\frac{me^4}{(4\pi\varepsilon_0)^2\cdot 2\hbar^2n^2}=-\frac{mc^2}{2}\cdot(\frac{e^2}{4\pi\varepsilon_0\hbar c})^2\cdot\frac{1}{n^2}=-\frac{1}{2}m(\alpha c\frac{Z}{n})^2
\end{aligned}\tag{50}$$
上两式中引入了一个新的无量纲常数,称为精细结构常数
$$\begin{aligned}
\frac{e^2}{4\pi\varepsilon_0\hbar c}\equiv \alpha \approx \frac{1}{137}
\end{aligned}\tag{51}$$
精细结构常数将电动力学量e,量子力学$\hbar$及相对论量c有机联系在了一起,它体现了原子光谱的精细结构的定量数值,但该常数的物理本质尚未清晰
由式子$(50)$可以看出,非相对情况下体系总能量的数值与电子动能的数值相等,因此量子化的电子速率为
$$\begin{aligned}
v_n=\alpha c\frac{Z}{n} \quad \beta=\alpha\frac{Z}{n}
\end{aligned}\tag{52}$$
下面按照相对论改写能量公式为
$$\begin{aligned}
E_n=(m-m_0)c^2-mc^2(\frac{\alpha Z}{n})^2=-m_0c^2+\frac{m_0c^2}{\sqrt{1-\beta^2}}[\sqrt{1-\beta^2}-1]
\end{aligned}\tag{53}$$
由于$0<\beta<<1$,级数展开,展开项最高阶数保留至二阶
$$\begin{aligned}
E_n=m_0c^2[1-\frac{1}{2}\beta^2-\frac{1}{8}\beta^4-1]=-m_0c^2[\frac{1}{2}\beta^2+\frac{1}{8}\beta^4]
\end{aligned}\tag{54}$$
$$\begin{aligned}
E_n=-\frac{m_0c^2}{2}(\frac{Z\alpha}{n}^2)[1+\frac{1}{4}(\frac{Z\alpha}{n}^2)]
\end{aligned}\tag{55}$$
可以看见,式中第一项是非相对论情况下的能量,但这仅仅是对圆轨道进行额修正考虑不同形状的轨道,则经过相对论修正后的氢原子的能量为
$$\begin{aligned}
E=-\mu c^2+\mu c^2[1+\frac{\alpha^2 Z^2}{[n_r+(n_{\phi}^2-\alpha^2Z^2)^{\frac{1}{2}}]^2}]^{-\frac{1}{2}}
\end{aligned}\tag{56}$$
$\mu$为两体问题的约化质量,做级数展开并保留到$\alpha^4$项可得相对论修正的光谱项公式
$$\begin{aligned}
\tilde{\nu}=T(n,n_{\phi})=-\frac{E}{hc}\approx \frac{RZ^2}{n^2}+\frac{RZ^4\alpha^2}{n^4}(\frac{n}{n_{\phi}}-\frac{3}{4})
\end{aligned}\tag{57}$$
显然光谱项决定于电子的轨道形状,也即与主量子数和角量子数有关
小结
精细结构常数
$$\begin{aligned}
\alpha=\frac{e^2}{4\pi\varepsilon_0\hbar c}\approx \frac{1}{137}
\end{aligned}$$
appendix
下面给出了两个前文标注锚点处的公式推导
- 椭圆极坐标表示的简易推导
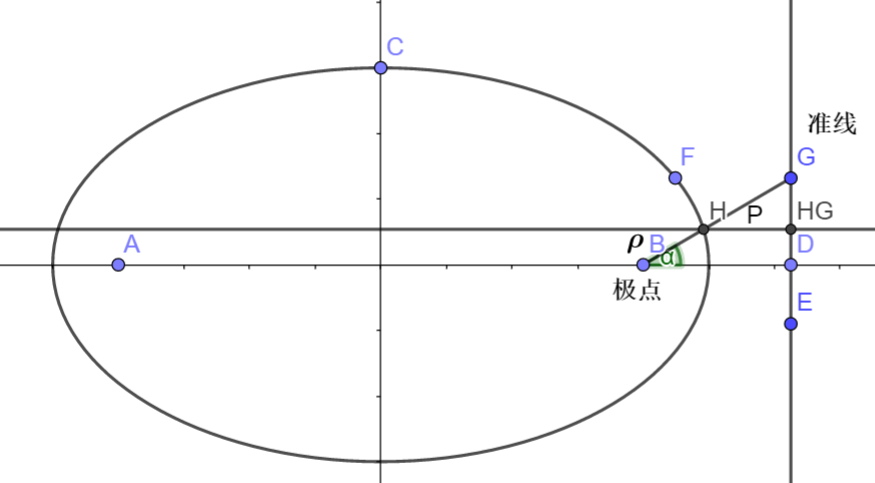
取其中一个焦点为极点,相关的参数已标注于图中
|BD|=P,$|BD|=\rho$
根据椭圆的第二定义,椭圆上一点到焦点的距离与其到焦点临近的准线的距离之比为离心率e
在标准笛卡尔坐标系下主线方程分别为
$$\begin{aligned}
x=\pm\frac{a^2}{c}
\end{aligned}$$
因此图中P表征为
$$\begin{aligned}
P=\frac{a^2}{c}-c=\frac{b^20}{c}
\end{aligned}$$
$$\begin{aligned}
P=\rho\cos\alpha+\frac{\rho}{e}
\end{aligned}$$
整理可得
$$\begin{aligned}
\rho=\frac{eP}{1+e\cos\alpha}=\frac{\frac{a^2-c^2}{a}}{1+e\cos\alpha}=\frac{a(1-e^2)}{1+e\cos\alpha}
\end{aligned}$$
至此,我们得到了椭圆的极坐标方程
$$\begin{aligned}
\rho=\frac{a(1-e^2)}{1+e\cos\alpha}
\end{aligned}$$
- 电子椭圆运动的半短轴与半长轴之比的证明
$$\begin{aligned}
\frac{b}{a}=\frac{n_{\phi}}{n_{\phi}+n_{r}}=\frac{n_{\phi}}{n}
\end{aligned}$$
利用量子化通则
$$\begin{aligned}
\oint p_{r}\mathrm{dr}=n_{r}h \quad p=m\dot{r}
\end{aligned}$$
利用椭圆极坐标方程
$$\begin{aligned}
\rho=\frac{a(1-e^2)}{1+e\cos\phi}
\end{aligned}$$
得到积分为
$$\begin{aligned}
\oint m\dot{r}\mathrm{dr}&=\oint m\frac{\mathrm{dr}}{\mathrm{dt}}\mathrm{dr}=\oint m\frac{\mathrm{dr}}{\mathrm{d\phi}}\frac{\mathrm{d\phi}}{\mathrm{dt}}\frac{\mathrm{dr}}{\mathrm{d\phi}}\mathrm{d\phi} \\
&=\oint m(\frac{\mathrm{dr}}{\mathrm{d\phi}})^2\dot{\phi}\mathrm{d\phi} \\
&=\oint m\big[ \frac{a(1-e^2)}{1+e\cos\phi} \big]^2\cdot\dot{\phi}\cdot e^2\sin^2\phi\mathrm{d\phi} \\
&=\oint mr^2\dot{\phi}\cdot\frac{e^2\sin^2\phi}{(1+e\cos\phi)^2}\mathrm{d\phi} \\
&=e^2p_{\phi}\int_{0}^{2\pi}\frac{\sin^2{\phi}}{(1+e\cos\phi)^2}\mathrm{d\phi} \\
&=e^2\frac{n_{\phi}h}{2\pi}\cdot\frac{2\pi}{e^2}(\frac{1}{\sqrt{1-e^2}}-1) \\
&=n_{\phi}h(\frac{a}{b}-1)
\end{aligned}$$
即
$$\begin{aligned}
n_{r}h=n_{\phi}h(\frac{a}{b}-1)
\end{aligned}$$
故
$$\begin{aligned}
\frac{b}{a}=\frac{n_{\phi}}{n_{\phi}+n_{r}}=\frac{n_{\phi}}{n}
\end{aligned}$$
量子力学导论
波粒二象性
- 光的波粒二象性
$$\begin{aligned}
\vec{p}=\hbar\vec{k}
\end{aligned}\tag{58}$$ - 物质的波粒二象性
- 德布罗意物质波假设
路易斯·维多克·德布罗意将量子理论与爱因斯坦的相对论进行结合,道出了著名的德布罗意关系式
$$\begin{aligned}
\lambda=\frac{h}{m_{0}v}\sqrt{1-(\frac{v}{c})^2}
\end{aligned}\tag{59}$$
并且指出,物质粒子具有质量就有能量,有能量就有频率,有频率就有波动
德布罗意假设的核心思想是一切实物粒子都具有波动性,与物质相联系的物质波的波长表示为
$$\begin{aligned}
\lambda=\frac{h}{p}
\end{aligned}\tag{60}$$
此式称为德布罗意关系,是在非相对论情况下的结果,该式与光的波粒二象性表达式完全一致 - 德布罗意物质波的实验验证
戴维孙-革末实验
设电子束垂直入射晶体表面,晶体中的原子间距为a,对某一晶面的散射角为$\theta$,晶体点阵犹如反射式衍射光栅,散射角$\theta$是对于某晶面的反射角与入射角之间的夹角,则入射角和反射角均为$\alpha=\frac{\theta}{2}$,相邻两个晶面的间距$d=a\sin\alpha$,而散射电子与入射电子之间的程差为$2d\cos\alpha$,则满足散射波加强的条件为
$$\begin{aligned}
n\lambda=2d\cos\alpha=2a\cos\alpha\sin\alpha=a\sin 2\alpha=a\sin\theta
\end{aligned}$$
即
$$\begin{aligned}
n\lambda=a\sin\theta
\end{aligned}\tag{61}$$
- 德布罗意物质波假设
波函数与态的叠加原理
波函数及其统计解释
奥地利物理学家欧文·薛定谔(E.Schrodinger)开创性地提出了微观世界中地位相当于牛顿第二定律的薛定谔方程.他和德布罗意一样,认为粒子是一个波包,引入波函数$\Psi(\vec{r},t)$来描述波包的运动状态,并认为$|\Psi(\vec{r},t)|^2$代表微观粒子在空间的密度,而$\Psi(\vec{r},t)$描写的是实在的波
把微观粒子的原子性与波的相干性叠加统一在一起的是英国物理学家马克斯·玻恩(M.Born).按照玻恩的统计解释,微观粒子的运动状态由波函数描述,,波函数$\Psi(\vec{r},t)$表示在t时刻出现在$\vec{r}$处粒子的概率波幅,而$|\Psi(\vec{r},t)|^2$表示在t时刻、位置$\vec{r}$处粒子出现的概率密度.任意粒子的波函数可以通过傅里叶变换展开成平面波的叠加形式,因此波函数一般采用复数形式.因此,$|\Psi(\vec{r},t)|^2=\Psi^{}(\vec{r},t)\cdot\Psi(\vec{r},t)$表示波函数的模方.但是玻恩的统计解释的适用范围还局限于非相对论情况
由概率论原理我们知道,若一个函数是概率密度函数,则其必须满足归一化条件,因此,在全空间中,粒子出现的总概率应当满足
$$\begin{aligned}
\int_{-\infty}^{\infty}|\Psi(\vec{r},t)|^2\mathrm{d\tau} = 1
\end{aligned}\tag{62}$$
此式称为波函数的*归一化条件.注意,上式中的积分微元$\mathrm{d\tau}$表示的是体积微元,体积微元的具体形式与空间坐标和具体坐标系有关.
对于概率分布来说,更为重要的是相对概率的分布.考虑两个仅差一个常数因子的波函数:$\Psi(\vec{r},t)$,$C\Psi(\vec{r},t)$,他们在同一时刻t、空间中任意两个位置$r_{1},r_{2}$处的相对概率为
$$\begin{aligned}
|\frac{\Psi(\vec{r_{1}},t)}{\Psi(\vec{r_{2}},t)}|^2\equiv|\frac{C\Psi(\vec{r_{1}},t)}{C\Psi(\vec{r_{2}},t)}|^2
\end{aligned}\tag{63}$$
上式表明,波函数允许相差一个常数因子,这与经典情况下的波是不同的,因为经典波不存在归一化问题,当波幅增大一倍时,能量会增大为原来的四倍,因此量子力学中的概率波完全不同于经典波.
量子力学的波函数要求满足归一化条件,该式要求波函数必须是平方可积的函数,但一般来说,任意波函数的模方在全空间的积分并不总是等于概率1,这时需要对波函数进行归一化,假设
$$\begin{aligned}
\int_{-\infty}^{\infty}|\Psi(\vec{r},t)|^2\mathrm{d\tau} = A
\end{aligned}\tag{64}$$
显然
$$\begin{aligned}
\int_{-\infty}^{\infty}|\frac{1}{\sqrt{A}}\Psi(\vec{r},t)|^2\mathrm{d\tau} = 1
\end{aligned}\tag{65}$$
因此这样就能得到归一化的波函数
按照波函数的统计解释,波函数还有两个重要性质,即连续型和单值性,这就是说波函数在全空间的分布必须是连续函数,也必须是单值函数
所以波函数必须满足三个标准条件:有界性,连续型,单值性态的叠加原理
假设$\Phi_{1}$、$\Phi_{2}$为描述粒子的两个不同状态的波函数,则他们的线性叠加
$$\begin{aligned}
\Psi=C_{1}\Phi_{1}+C_{2}\Phi_{2}
\end{aligned}\tag{66}$$
的含义为线性叠加态$\Psi=C_{1}\Psi_{1}+C_{2}\Psi_{2}$表示粒子既可能处于$\Psi_{1}$态又可能处于$\Psi_{2}$态,处于这两个态的概率分别为$|C_{1}|^2$、$|C_{2}|^2$.线性叠加原理可以推广到多个态的情况描述粒子状态的波函数和态的叠加原理是量子力学的一个基本假设
小结
$\Psi(\vec{r},t)$表示概率波幅,$|\Psi(\vec{r},t)|^2$表示概率密度
波函数需要满足三个条件:单值性、有界性和连续型
波函数允许相差一个常数因子,他们描述的相对概率完全相同
波函数具有线性叠加性,这是量子力学的一个基本假设
薛定谔方程的建立及其性质
- 在之前很多的文章中,都提及过平面电磁波方程
$$\begin{aligned}
\Psi(\vec{r},t)=A\cos(\vec{k}\cdot\vec{r}-\omega t)
\end{aligned}\tag{67}$$
我们说过,在实际应用中,我们更偏爱该方程的复数形式
$$\begin{aligned}
\Psi(\vec{r},t)=Ae^{i(\vec{k}\cdot\vec{r}-\omega t)}
\end{aligned}\tag{68}$$
我们知道自由粒子的能量和动量之间满足如下关系
$$\begin{aligned}
E=\frac{P^2}{2m}
\end{aligned}\tag{69}$$
根据爱因斯坦-德布罗意关系
$$\begin{aligned}
E=\hbar\omega \quad \vec{p}=\hbar\vec{k}
\end{aligned}\tag{70}$$
将$(70)$代入$(68)$便得到
$$\begin{aligned}
\Psi(\vec{r},t)=Ae^{\frac{i}{\hbar}(\vec{P}\cdot\vec{r}-Et)}
\end{aligned}\tag{71}$$
上式就是自由粒子的波函数表达式
对上式取偏微分可以得到如下结果
$$\begin{cases}
i\hbar\frac{\partial \Psi}{\partial t}=E\Psi \\
-i\hbar\nabla\Psi=\vec{p}\Psi \\
-\hbar^2\nabla^2\Psi=p^2\Psi
\end{cases}$$
代入式$(69)$可知
$$\begin{aligned}
(E-\frac{p^2}{2m})\Psi=(i\hbar\frac{\partial }{\partial t}+\frac{\hbar^2}{2m}\nabla^2)\Psi=0
\end{aligned}$$
即
$$\begin{aligned}
i\hbar\frac{\partial }{\partial t}\Psi=-\frac{\hbar^2}{2m}\nabla^2\Psi
\end{aligned}\tag{72}$$
该方程表示自由粒子的波函数随时间演化的规律,称为自由粒子的薛定谔方程
对比式$(69)$,我们可以进行算符替换,即
$$\begin{aligned}
E\rightarrow i\hbar\frac{\partial }{\partial t} \quad \vec{p}\rightarrow -i\hbar\nabla
\end{aligned}\tag{73}$$
替代后的运算符号称为算符,替代能量的算符称为能量算符,替代动量的算符称为动量算符.当然,由于能量与动量之间存在关系,显然能量算符还有另外一个表达式
$$\begin{aligned}
E=\frac{p^2}{2m}=\frac{\vec{p}\cdot\vec{p}}{2m}=-\frac{\hbar^2}{2m}\nabla^2
\end{aligned}\tag{74}$$
植入回顾
在光的电磁波理论一文中,我们也有算符替换
$\nabla \rightarrow i\vec{k}$
$\nabla \cdot \rightarrow i\vec{k}\cdot$
$\nabla \times \rightarrow i\vec{k}\times$
$\frac{\partial }{\partial t} \rightarrow -i\omega$
推广的薛定谔方程及其性质
一般形式的薛定谔方程
一般情况下,粒子的能量由动能和势能构成.上文中的自由粒子不存在势能项,但更为一般的情形下,粒子是具有势能项的,因此
$$\begin{aligned}
E=\frac{p^2}{2m}+V(\vec{r},t)
\end{aligned}\tag{75}$$
则薛定谔方程写为
$$\begin{aligned}
i\hbar\frac{\partial }{\partial t}\Psi=-\frac{\hbar^2}{2m}\nabla^2\Psi+V\Psi
\end{aligned}\tag{76}$$定域的概率守恒
在非相对论情况下,不涉及实物粒子的产生和湮灭现象,所以在随时间演化的过程中,粒子数目保持不变.下面从薛定谔方程导出概率守恒定律
在式$(76)$中,取复共轭有
$$\begin{aligned}
-i\hbar\frac{\partial }{\partial t}\Psi^{\star}=(-\frac{\hbar^2}{2m}\nabla^2+V)\Psi^{\star}
\end{aligned}\tag{77}$$
下面是数学把戏时间
将$\Psi^{\star}\times(76)-\Psi\times(77)$得到
$$\begin{aligned}
i\hbar\frac{\partial }{\partial t}(\Psi\Psi^{\star}) &=-\frac{\hbar^2}{2m}(\Psi^{\star}\nabla^2\Psi-\Psi\nabla^2\Psi^{\star}) \\
&=-\frac{\hbar^2}{2m}\nabla\cdot(\Psi^{\star}\nabla\Psi-\Psi\nabla\Psi^{\star})
\end{aligned}\tag{78}$$
根据Gauss定理对上式两侧进行体积分
$$\begin{aligned}
i\hbar\frac{\partial }{\partial t}\int\Psi\Psi^{\star}\mathrm{dV}=-\frac{\hbar^2}{2m}\oint(\Psi^{\star}\nabla\Psi-\Psi\nabla\Psi^{\star})\cdot\mathrm{d\vec{S}}
\end{aligned}\tag{79}$$
下面引入两个量:概率密度和概率流密度矢量
$$\begin{aligned}
\rho(\vec{r},t)=\Psi^{\star}(\vec{r},t)\Psi(\vec{r},t)
\end{aligned}\tag{80}$$
$$\begin{aligned}
\vec{j}(\vec{r},t)=-\frac{i\hbar}{2m}(\Psi^{\star}\nabla\Psi-\Psi\nabla\Psi^{\star})
\end{aligned}\tag{81}$$
因此式$(79)$可以化为
$$\begin{aligned}
\frac{\mathrm{d}}{\mathrm{dt}}\int\rho\mathrm{dV}=-\oint\vec{j}\cdot\mathrm{d\vec{S}}
\end{aligned}\tag{82}$$
式$(82)$即为定域粒子的概率守恒的积分形式,又称粒子数守恒定律,其物理意义是在一个定域的闭区域中找到粒子的总概率在单位时间内的增量等于从该封闭表面流入该区域内的粒子概率
利用Gauss定理,可以得到粒子数守恒定律的微分形式
$$\begin{aligned}
\frac{\partial }{\partial t}\rho+\nabla\cdot\vec{j}=0
\end{aligned}\tag{83}$$
上式称为粒子数守恒的连续性方程,与流体力学中的连续性方程形式相同.上式的物理意义为:在空间中任意一点处及其附近的粒子概率随时间变化,则必然有一定概率的粒子从该点流出或从其他地方流入.定量地讲,空间某点及其附近的粒子概率随时间的增加(或减少)等于外界流入到该点(或由该点流出)的粒子概率
如果考虑粒子的边界在无限远处,那么对空间的积分就拓展到全空间.因为波函数具有有界性,波函数在边界上的数值等于零,即在编辑处,粒子流密度为零,于是有
$$\begin{aligned}
\frac{\mathrm{d}}{\mathrm{dt}}\int_{全}|\Psi(\vec{r},t)|^2\mathrm{dV}=0
\end{aligned}$$
也就是说,全空间的粒子总概率不随时间变化,实际上就是全空间找到粒子的总概率等于1(归一化条件).在物理上表示粒子既不会产生,也不会消失
能量本征方程和本征态
对于一般形式的薛定谔方程,如果势函数不是时间的显函数或与时间无关,那么我们便可以将波函数分解为空间和时间两个单独参变量函数的乘积,即得到
$$\begin{aligned}
\Psi(\vec{r},\vec{t})=\phi(\vec{r}) \cdot f(t)
\end{aligned}$$
$$\begin{aligned}
\frac{i\hbar}{f(t)}\frac{\mathrm{df}}{\mathrm{dt}}=\frac{1}{\phi(\vec{r})}[-\frac{\hbar^2}{2m}\nabla^2+V(\vec{r})]\phi(\vec{r})
\end{aligned}\tag{84}$$
上式左侧是时间的函数,右侧是空间的函数,等式恒等的条件显然是等于同一个常数
事实上,这种方法我们再熟悉不过了,更多详情请看数学物理方法中的讲述
波函数代表概率幅,是无量纲量,通过量纲分析,显然该恒等的常数应该具有能量的量纲,因此上式分离为两个方程
$$\begin{aligned}
\frac{i\hbar}{f}\frac{\mathrm{df}}{\mathrm{dt}}=E
\end{aligned}\tag{85}$$
$$\begin{aligned}
[-\frac{\hbar^2}{2m}\nabla^2+V]\phi=E\phi
\end{aligned}\tag{86}$$
式$(85)$的通解为$e^{-\frac{iEt}{\hbar}}+C$,讲积分常数归并到空间波函数中,波函数因此写为
$$\begin{aligned}
\Psi(\vec{r},t)=\phi(\vec{r})e^{-\frac{iEt}{\hbar}}
\end{aligned}\tag{87}$$
对于任意常数E,式$(86)$在数学角度上似乎可以解出波函数,然而,量子力学的波函数表示粒子出现的概率幅,它必须满足三个标准条件(有界性,单值性,连续性),因此考虑实际问题时能够满足波函数要求的解就限制了E不会连续变化,而是取一些离散的值.这些离散的能量称为体系的本征能量值,又称能量的量子化.相应的波函数空间解称为体系的能量本征函数或能量本征态,式$(86)$称为势场V中粒子运动的能量本征方程,又称不含时薛定谔方程或定态薛定谔方程通过算符替换,我们可以通过经典力学的Hamilton能量表达式得到量子力学中的Hamilton算符
$$\begin{aligned}
\hat{H}=-\frac{\hbar^2}{2m}\nabla^2+V(\vec{r})
\end{aligned}\tag{88}$$
将Hamilton算符代入$(86)$式得到如下形式的能量本征方程
$$\begin{aligned}
\hat{H}\Psi=E\Psi
\end{aligned}\tag{89}$$
在量子力学的矩阵力学形式中,力学算符可以表示成方阵,波函数可以表示为列矩阵,上述方程可以等价于一个矩阵本征方程,这也是为什么称之为本征方程用Hamilton算符表示含时薛定谔方程
$$\begin{aligned}
i\hbar\frac{\partial }{\partial t}\Psi(\vec{r},t)=\hat{H}\Psi(\vec{r},t)
\end{aligned}\tag{90}$$因此,对于不显含时间的势函数,只需要求解出能量的本征方程,解出本征函数后就可以得到体系的波函数,这样的波函数所描述的状态称为定态
定态具有以下特征- 粒子的概率密度和粒子的概率流密度不随时间变化
- 任何不显含时间的力学量的平均值不随时间变化
- 任何不显含时间的力学量的测量值的概率分布也不随时间变化
- 属于不同能量本征值的两个本征函数彼此时正交归一化的
小结
量子力学的算符替代:$E\rightarrow i\hbar\frac{\partial }{\partial t}$,$\vec{p}\rightarrow -i\hbar\nabla$
薛定谔方程的一般形式:$i\hbar\frac{\partial }{\partial t}\Psi(\vec{r},t)=[-\frac{\hbar^2}{2m}\nabla^2+V(\vec{r},t)]\Psi(\vec{r},t)$
概率密度:$\Psi^{*}\Psi$
概率流密度矢量:$\vec{j}=-\frac{i\hbar}{2m}(\Psi^{\star}\nabla\Psi-\Psi\nabla\Psi^{\star})$
粒子数守恒定律微分形式:$\frac{\partial }{\partial t}\rho+\nabla\cdot\vec{j}=0$
一维定态薛定谔方程
粒子在一维势场V(x)中运动,在一维情况下,粒子运动状态满足的定态薛定谔方程为
$$\begin{aligned}
[-\frac{\hbar^2}{2m}\frac{\mathrm{d^2}}{\mathrm{dx^2}}+V(x)]\Psi(x)=E\Psi(x)
\end{aligned}\tag{91}$$
这是一个二阶常微分方程下面介绍几种简单实用的一维问题
一维无限深势阱
- 物理模型
质量为m的粒子处在一维无限深势阱中运动,势函数用下式表示
$$V(x)=\begin{cases}
0,\quad 0\le x\le a \\
\infty, \quad x<0, x>a
\end{cases}$$
式中,a为势阱的宽度;V(x)为势阱的深度,在阱内势能等于零,在阱外势能无穷大 - 薛定谔方程
根据一维情况下的薛定谔方程式式$(91)$,可以分别写出一维无限深势阱内外的薛定谔方程
(1) 在阱内的薛定谔方程为
$$\begin{aligned}
-\frac{\hbar^2}{2m}\frac{\mathrm{d^2}}{\mathrm{dx^2}}\Psi_{1}=E\Psi_{1} \quad 0\le x\le a
\end{aligned}\tag{92}$$
(2) 在阱外的薛定谔方程为
$$\begin{aligned}
-\frac{\hbar^2}{2m}\frac{\mathrm{d^2}}{\mathrm{dx^2}}\Psi_{2}+\infty\cdot\Psi_{2}=E\Psi_{2} \quad else
\end{aligned}\tag{93}$$
由波函数的连续性得到边界条件为
$$\begin{aligned}
\Psi_{1}(0)=\Psi_{2}(0) ,\quad \Psi_{1}(a)=\Psi_{2}(a)
\end{aligned}$$ - 方程的解
解阱外薛定谔方程程式$(93)$,由于波函数的有界性要求,粒子无法穿过无限深势阱,因此势阱外的解为
$$\begin{aligned}
\Psi_{2}(x)=0
\end{aligned}$$
解阱内薛定谔方程程式$(92)$,作如下替换
$$\begin{aligned}
k^2=\frac{2mE}{\hbar^2}
\end{aligned}\tag{94}$$
原式化为
$$\begin{aligned}
\Psi_{1}’’+k^2\Psi_{1}=0
\end{aligned}$$
该二阶常系数微分方程的解显然为
$$\begin{aligned}
\Psi_{1}(x)=A\cos(kx)+B\sin(kx)
\end{aligned}$$
由边界条件可以确定系数
$$\begin{aligned}
\Psi_{1}(0)=0 \Rightarrow A=0 \quad \Psi_{1}(a)=0 \Rightarrow ka=n\pi,n=1,2,\cdots
\end{aligned}$$
应当注意n=0,则k=0,则E=0,此时不代表粒子运动,而n取负整数,不能得到新的能量结果
由此,我们可得式$(94)$中的能量的表达式
$$\begin{aligned}
E=\frac{n^2\hbar^2\pi^2}{2ma^2}, \quad n=1,2,3,\cdots
\end{aligned}\tag{95}$$
式中n是正整数,可以看出能量是量子化的,而相应的波函数为
$$\begin{aligned}
\Psi_{1}(x)=B\sin(\frac{n\pi}{a}x) \quad (0\le x\le a)
\end{aligned}$$
波函数的归一化要求,概率密度全域积分为概率1,即
$$\begin{aligned}
\int_{0}^{a} B^2\sin^2(\frac{n\pi}{a}x)\mathrm{dx}=\frac{a}{2}\cdot B^2=1
\end{aligned}$$
因此归一化系数为
$$\begin{aligned}
B=\sqrt{\frac{2}{a}}
\end{aligned}$$
最终,势阱内外的归一化的波函数为
$$\Psi(x)=\begin{cases}
\sqrt{\frac{2}{a}}\sin\frac{n\pi}{a}x \quad 0\le x\le a\quad n\in Z^{+} \\
0 \quad x<0 , x>a
\end{cases}\tag{96}$$ - 讨论
- 由式$(95)$可知,粒子的最低能量为$E_{1}=\frac{\hbar^2\pi^2}{2ma^2}\neq 0$,这与经典粒子不同,这是微观粒子波粒二象性的表现,在微观世界中,静止的波是没有意义的,把体系中能量最低的状态称为基态,此后的状态分别称为第一激发态、第二激发态…
- 势阱内粒子的波函数是正弦形式,概率密度为
$$\begin{aligned}
|\Psi(x)|^2=\frac{2}{a}\sin^2(\frac{n\pi}{a}x)
\end{aligned}$$
显然,粒子在势阱内的概率分布和量子数n有关.我们把概率密度等于零的点称为节点,对于一个特定的n,节点数等于n-1.
- 物理模型
势垒的贯穿——量子隧穿效应
前言
1956年日本物理学家发现了隧道二极管;1960年美国物理学家加埃沃发现了超导体中的隧道贯穿;随后英国物理学家约瑟夫森从理论上预言了约瑟夫森隧道效应现象.1983年德国科学家宾尼和瑞士科学家罗雷尔研制出第一代扫描隧道电镜,此后,人们可以通过扫描隧道显微镜和原子力显微镜观察到物体表面的原子结构.
下面我们便从一维势垒简单阐述量子隧道效应物理模型
一维势垒将一维空间划分成三个区域Ⅰ、Ⅱ、Ⅲ,各个区域的势场为
$$V(x)=\begin{cases}
0,\quad x<0 \quadⅠ\\
U_{0} \quad 0\le x\le a \quadⅡ\\
0 \quad x\ge a \quadⅢ
\end{cases}\tag{97}$$薛定谔方程及其解
在势垒外的薛定谔方程为
$$\begin{aligned}
-\frac{\hbar^2}{2m}\frac{\mathrm{d^2}}{\mathrm{dx^2}}\Psi=E\Psi
\end{aligned}\tag{98}$$
与前文类似变换得到
$$\begin{aligned}
\frac{\mathrm{d^2}}{\mathrm{dx^2}}\Psi+k^2\Psi=0
\end{aligned}$$
他有两个线性无关的解取为$e^{\pm ikx}$,假设粒子从左入射,那么在Ⅰ区内$e^{ikx}$代表入射波,$e^{-ikx}$代表反射波.在Ⅲ区内,只有透射波$e^{ikx}$
因此,式$(97)$的解可以采用下述形式
$$\Psi(x)=\begin{cases}
e^{ikx}+R^{-ikx} ,\quad x<0 \\
Se^{ikx} ,\quad x>a
\end{cases}\tag{99}$$
式中,入射波波幅取为1是为了方便,R、S分别表示反射和透射波的波幅
利用式$(81)$概率流密度矢量公式分别用于此处的入射波、反射波和透射波,可得
式$(81)$为
$$\begin{aligned}
\vec{J}=-\frac{i\hbar}{2m}(\Psi^{\star}\nabla\Psi-\Psi\nabla\Psi^{\star})=\frac{\hbar}{m}Im(\Psi^{\star}\nabla\Psi)
\end{aligned}$$$$\begin{aligned}
&入射粒子流密度: j_{i}=\frac{\hbar}{m}k=v \\
&反射粒子流密度: j_{r}=|R|^2v \\
&透射粒子流密度: j_{t}=|S|^2v \\
\end{aligned}$$
则反射和透射系数分别为$\frac{j_{r}}{j_{i}}=|R|^2$,$\frac{j_{t}}{j_{i}}=|S|^2$
在势垒内部的薛定谔方程为
$$\begin{aligned}
[-\frac{\hbar^2}{2m}\frac{\mathrm{d^2}}{\mathrm{dx^2}}+U_{0}]\Psi=E\Psi
\end{aligned}\tag{100}$$
等价为
$$\begin{aligned}
\frac{\mathrm{d^2}}{\mathrm{dx^2}}\Psi-\frac{2m}{\hbar^2}(U_{0}-E)\Psi=0
\end{aligned}$$
等价为
$$\begin{aligned}
\frac{\mathrm{d^2}}{\mathrm{dx^2}}\Psi-k’^2\Psi=0
\end{aligned}$$
方程的通解为
$$\begin{aligned}
\Psi=Ae^{k’x}+Be^{-k’x}
\end{aligned}$$
在x=0处,由波函数的连续性有边界条件
$$\begin{aligned}
1+R=A+B
\end{aligned}\tag{B.C.1}$$
在x=0处,由波函数导数的连续性条件有边界条件3
$$\begin{aligned}
ik(1-R)=k’(A-B)
\end{aligned}\tag{B.C.1}$$
同样在x=a处,有波函数和波函数导数的连续性可得
$$\begin{aligned}
Ae^{k’a}+Be^{-k’a}=Se^{ika}
\end{aligned}\tag{B.C.2}$$
$$\begin{aligned}
K’(Ae^{ik’a}-Be^{-ik’a})=ikSe^{ika}
\end{aligned}\tag{B.C.2}$$
有两组边界条件$(B.C.1)$,$(B.C.2)$联立消去A,B得到关于R,S的方程组为
$$\begin{cases}
(1+\frac{ik}{k’})+R(1-\frac{ik}{k’})=S(1+\frac{ik}{k’})e^{ika-k’a} \\
(1-\frac{ik}{k’})+R(1+\frac{ik}{k’})=S(1-\frac{ik}{k’})e^{ika+k’a}
\end{cases}\tag{101}$$
对上式进一步分析推导,我们可以得到下面的关系
$$\begin{aligned}
|R|^2+|S|^2=1
\end{aligned}\tag{102}$$
即反射系数和透射系数之和等于1,说明从Ⅰ区入射的粒子,部分被反射回去,其余的贯穿势垒区Ⅱ而投射到Ⅲ区,通常,透射系数不为零.粒子能透射比它动能更高的势垒的现象称为隧道效应
隧道效应是量子力学中特有的物理现象,这是正微观粒子波动性的表现
一维谐振子
- 经典弹簧振子
由于十分熟悉,这里边一笔带过了.
在力学中,一个劲度系数为为K,质量为m的弹簧振子的体系总能量为
$$\begin{aligned}
E&=T+V=\frac{1}{2}m\dot{x}^2+\frac{1}{2}m\omega^2x^2 \\
&=\frac{1}{2}m[-A\omega A\sin(\omega t+\varphi)]^2+\frac{1}{2}m\omega^2[A\cos(\omega t+\varphi)]^2
&=\frac{1}{2}m\omega^2A^2
\end{aligned}$$ - 量子力学中谐振子
将一维谐振子的经典能量表达式改写成哈密顿算符
$$\begin{aligned}
\hat{H}=-\frac{\hbar^2}{2m}\frac{\mathrm{d^2}}{\mathrm{dx^2}}+\frac{1}{2}m\omega^2x^2
\end{aligned}$$
势函数不显含时间,是定态的,则相应的定态薛定谔方程为
$$\begin{aligned}
[-\frac{\hbar^2}{2m}\frac{\mathrm{d^2}}{\mathrm{dx^2}}+\frac{1}{2}m\omega^2x^2]\Psi(x)=E\Psi(x)
\end{aligned}\tag{103}$$
这是一个变系数二阶常微分方程
理想的谐振子,它的势场是一个无限深势阱,只存在束缚态,满足自然边界条件,即在$|x|\rightarrow\pm\infty,\Psi(x)\rightarrow 0$
下面引入两个无量纲参量
$$\begin{aligned}
\xi=\alpha x (\alpha=\sqrt{\frac{m\omega}{\hbar}}) \quad \lambda=\frac{2E}{\hbar\omega}
\end{aligned}$$
对上式进行无量纲化后微分方程变为
$$\begin{aligned}
\frac{\mathrm{d^2}}{\mathrm{d\xi^2}}\Psi+(\lambda-\xi^2)\Psi=0
\end{aligned}\tag{104}$$
这个二阶变系数微分方程中$\xi=\pm\infty$是它的非正则奇点.
当$\xi\rightarrow\pm\infty$时,方程的近似解为$\Psi(\xi)=e^{\pm\frac{\xi^2}{2}}$
由于波函数的有界性要求,故只有负指数的解满足有界性条件,于是式$(104)$的解可以表示为
$$\begin{aligned}
\Psi(\xi)=e^{-\frac{\xi^2}{2}}H(\xi)
\end{aligned}\tag{105}$$
代入式$(104)$即得
$$\begin{aligned}
\frac{\mathrm{d^2}}{\mathrm{d\xi^2}}H-2\xi\frac{\mathrm{d}}{\mathrm{d\xi}}H+(\lambda-1)H=0
\end{aligned}\tag{106}$$
这便是数学物理方程中的厄米方程.它仍是变系数的二阶常微分方程.其解法请在appendix中参见4
通过幂级数解分析可以发现其解的渐进行为是$H(\xi)\rightarrow e^{\xi^2}$
因此在$\xi\rightarrow\pm\infty$,体系的波函数$\Psi(x)\rightarrow e^{\frac{\xi^2}{2}}\rightarrow\infty$,不满足波函数的有界性要求.为保证波函数的有界性,便要要求$H(\xi)$不能是无穷级数,而当满足特定的条件时中断成一个多项式,该条件是
$$\begin{aligned}
\lambda-1=2n \quad n=0,1,2,\cdots
\end{aligned}\tag{107}$$
这样就得到一个多项式的解,即为$H_{n}(\xi)$,称为厄米多项式
将$\lambda=\frac{2E}{\hbar\omega}$与上面的条件联立即得谐振子能量公式
$$\begin{aligned}
E=E_{n}=(n+\frac{1}{2})\hbar\omega ,\quad n=0,1,2,\cdots
\end{aligned}\tag{108}$$
这就是谐振子的本征能量,也是量子化的,它由一系列均匀分布的能级组成,相邻两个能级之间的间隔等于$\hbar\omega$
厄米多项式的表达式为
$$\begin{aligned}
H_{n}(\xi)=(-1)^{n}e^{\xi^2}\frac{\mathrm{d^n}}{\mathrm{d\xi^n}}e^{-\xi^2}
\end{aligned}\tag{109}$$
它的正交性公式为
$$\begin{aligned}
\int_{-\infty}^{\infty}H_{m}(\xi)H_{n}(\xi)e^{-\xi^2}\mathrm{d\xi}=\sqrt{\pi}2^n\cdot n!\delta_{mn}
\end{aligned}\tag{110}$$
正交归一的波函数为
$$\begin{aligned}
\Psi_{n}(\alpha x)=[\frac{\alpha}{\pi^{\frac{1}{2}}2^n\cdot n!}]^{\frac{1}{2}}e^{-\frac{\alpha^2x^2}{2}}H_{n}(\alpha x)
\end{aligned}\tag{111}$$
其正交归一关系为
$$\begin{aligned}
\int_{-\infty}^{\infty}\Psi_{m}(\xi)\Psi_{n}(\xi)\mathrm{dx}=\delta_{mn}
\end{aligned}\tag{112}$$
上面用到了克罗内克符号$\delta_{mn}$
$$\delta_{mn}=\begin{cases}
1 ,\quad m=n \\
0 ,\quad m\neq n
\end{cases}$$
厄米多项式有两个重要的递推关系
$$\begin{aligned}
H_{n+1}(\xi)-2\xi H_{n}(\xi)+3nH_{n-1}(\xi)=0
\end{aligned}\tag{113}$$
$$\begin{aligned}
\frac{\mathrm{d}H_{n}(\xi)}{\mathrm{d}\xi}=2nH_{n-1}(\xi)
\end{aligned}\tag{114}$$
- 总结
- 基态能量:$E_{0}=\frac{\hbar\omega}{2}$不等于零,称为零点能.这也是微观粒子波粒二象性的表现
- 波函数具有以下性质:
$\Psi_{n}(-x)=(-1)^{n}\Psi_{n}(x)$,即当n为奇数时,波函数是奇函数;当n为偶数时,波函数是偶函数.
我们把波函数具有确定的奇偶性称为体系具有确定的宇称,奇函数对应奇宇称,偶函数对应偶宇称.
体系具有确定的宇称是由体系中的势函数具有空间反演对称性决定的.因为谐振子的势函数是偶函数,因此它必有确定的宇称 - 当体系处于基态时,基态谐振子在空间中的概率分布为
$$\begin{aligned}
|\Psi_{0}(x)|^2=\frac{\alpha}{\sqrt{\pi}}e^{-\alpha^2x^2}
\end{aligned}$$
- 经典弹簧振子
appendix
此处给出锚点3,锚点4的说明
- 关于波函数一阶导数的连续性问题的证明请自寻CNKI
- 厄米方程的幂级数求解法
$$\begin{aligned}
\frac{\mathrm{d^2}}{\mathrm{d\xi^2}}H(\xi)-2\xi\frac{\mathrm{d}}{\mathrm{d\xi}}H(\xi)+(\lambda-1)H=0
\end{aligned}\tag{A-1}$$
将$H(\xi)$在常点$\xi=0$的邻域内展开成幂级数
$$\begin{aligned}
H(\xi)=\sum_{k=0}^{\infty}c_{k}\xi^{k}
\end{aligned}\tag{A-2}$$
将$(A-2)$代入$(A-1)$得
$$\begin{aligned}
\sum_{k=2}^{\infty}c_{k}k(k-1)\xi^{k-2}-2\sum_{k=1}^{\infty}c_{k}k\xi^{k}+(\lambda-1)\sum_{k=0}c_{k}\xi^{k}=0
\end{aligned}$$
上式是恒等条件式,则同次幂的系数必须为零,对k次幂的系数有
$$\begin{aligned}
(k+2)(k+1)c_{k+2}-2kc_{k}+(\lambda-1)c_{k}=0
\end{aligned}$$
于是偶次幂的递推关系为
$$\begin{aligned}
c_{k+2}=\frac{2k-(\lambda-1)}{(k+1)(k+2)}c_{k} ,\quad k=0,1,2,\cdots
\end{aligned}\tag{A-3}$$
因此可以用$c_0$来表征所有偶次幂项的系数,用$c_{1}$来表征所有奇次幂的系数,则厄米方程有两个线性无关的解
$$\begin{aligned}
H(\xi)=c_{0}+c_{2}\xi^2+c_{4}\xi^4+\cdots
\end{aligned}\tag{A-4}$$
$$\begin{aligned}
H(\xi)=c_{1}\xi+c_{3}\xi^3+c_{5}\xi^{5}+\cdots
\end{aligned}\tag{A-5}$$
下面讨论两个级数解的收敛情况- 当$\xi$取有限值时,$\lim_{k\to \infty}\frac{c_{k+2}}{c_{k}}=0$,因此两个级数都收敛
- 当$|\xi|\rightarrow\infty$时,当$k\rightarrow\infty$,$\frac{c_{k+2}}{c_{k}}\approx \frac{2}{k}$
则$\frac{c_{2m+2}}{c_{2m}}\approx\frac{1}{m}$,因此偶此项幂级数的收敛行为与$e^{\xi^2}=\sum_{m=0}^{\infty}\frac{\xi^{2m}}{m!}$一致,故$H(\xi)\propto e^{\xi^2}$;同理,奇次幂项解$H(\xi)\propto \xi e^{\xi^2}$.因此,在无穷远处不满足波函数有界性的要求.因此,只有当系数的递推关系式$(A-3)$中$2k=\lambda-1$时,无穷级数解$(A-4),(A-5)$中至少一个为多项式时,多项式形式的解才是物理上可以接受的解.也就是说,当满足
$$\begin{aligned}
\lambda-1=n ,\quad n=0,1,2,\cdots
\end{aligned}\tag{A-6}$$
时,级数解$(A-4)$中,n取偶数,$c_{n+2}$以后的偶此项全部为零而截断称为一个多项式,对级数解$(A-5)$同理.
习惯上,规定多项式的最高次项为$c_{n}=2^n$,相当于$c_{0}=1,c_{1}=2$,因此n次多项式的全部系数可由递推关系式给出,得到如下的多项式
$$\begin{aligned}
H_{n}(\xi)=(2\xi)^n-n(n-1)(2\xi)^{n-2}+\cdots+(-1)^{[\frac{n}{2}]}\frac{n!}{[\frac{n}{2}]!}(2\xi)^{n-2[\frac{n}{2}]}
\end{aligned}\tag{A-7}$$
式中
$$[\frac{n}{2}=]\begin{cases}
\frac{n}{2}\quad n为偶数 \\
\frac{n-1}{2} \quad n为奇数
\end{cases}$$
这就是厄米多项式
量子力学导论小结
- 微观粒子具有波粒二象性,波动性和粒子性是物质矛盾二重性的表现.波粒二象性统一在爱因斯坦-德布罗意关系中
$$\begin{aligned}
E=\hbar\omega \quad \vec{p}=\hbar\vec{k}
\end{aligned}$$- 微观粒子的状态用波函数$\Psi(\vec{r},t)$表示.$|\Psi(\vec{r},t)|^2$表示在t时刻,位置$\vec{r}$处找到粒子的概率.根据波函数的统计解释,波函数应当满足有界性,连续性和单值性.波函数又称态函数,满足叠加原理
- 自由粒子运动满足薛定谔方程
$$\begin{aligned}
i\hbar\frac{\partial }{\partial t}\Psi=[-\frac{\hbar^2}{2m}\nabla^2+V]\Psi
\end{aligned}$$
若势函数与时间无关,则通过分离变量拆分为时间和空间的常微分方程.
时间部分的解都是$f(t)=e^{-\frac{iEt}{\hbar}}$
空间部分满足能量本征方程$\hat{H}\Psi=E\Psi$- 宽度为a的无限深势阱的能量为
$$\begin{aligned}
E=\frac{n^2\hbar^2\pi^2}{2ma^2},\quad an=1,2,\cdots
\end{aligned}$$
归一化波函数为
$$\begin{cases}
\Psi_{1}(x)=\sqrt{\frac{2}{a}}\sin\frac{n\pi}{a}x \quad 势阱内 \\
\Psi_{2}(x)=0 \quad 势阱外
\end{cases}$$- 宽度为a,高度为$U_0$的势垒中反射与透射系数满足
$$\begin{aligned}
|R|^2+|S|^2=1
\end{aligned}$$
其中反射系数与透射系数分别为
$$\begin{aligned}
|R|^2=\frac{(k^2+k’^2) sh^2(k’a)}{(k^2+k’^2)^2 sh^2(k’a)+4k^2k’^2}
\end{aligned}$$
$$\begin{aligned}
|S|^2=\frac{4k^2k’^2}{(k^2+k’^2)^2 sh^2(k’a)+4k^2k’^2}
\end{aligned}$$
能量低于势垒高度的微观粒子能穿透势垒的现象称为量子隧道效应.量子隧道效应是扫描隧道显微镜的基础.- 一维谐振子的本征能量为
$$\begin{aligned}
E=E_{n}=(n+\frac{1}{2})\hbar\omega \quad n=0,1,2,\cdots
\end{aligned}$$
相应的归一化本征波函数为
$$\begin{aligned}
\Psi_{n}(\alpha x)=[\frac{\alpha}{\pi^{\frac{1}{2}}2^n\cdot n!}]^{\frac{1}{2}}e^{-\frac{\alpha^2x^2}{2}}H_{n}(\alpha x)
\end{aligned}$$
一维谐振子存在零点能$E_0=\frac{1}{2}\hbar\omega$,且在经典禁区也有15.7%的概率,这是经典理论物理解释的.

This is an identification card as an honored membership of FeynmanDirac
Happy to see you follow FeynmanDirac, enjoy science together
 验证码启动中...
验证码启动中...
备用人机验证