模拟集成电路中的单元电路
请注意,本文最近一次更新于:2021-11-17,文章内容可能已经不具有时效性,请谨慎参考
本文最后更新于:2021年11月17日星期三晚上11点05分 +08:00
电流源和电流镜
双极型电流源
由两个结构相同的双极晶体管组成的简单电流源如下所示
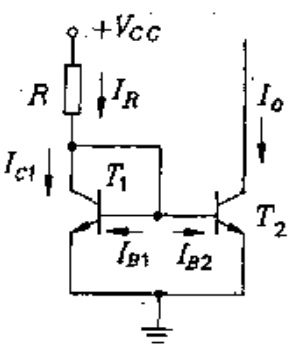
其中$T_1$管的基极-集电极B、C短接,工作于正向放大区,且$V_{BE1}=V_{BE2}$,为此我们可以得到如下分析
$$\begin{equation}
I_{C1}=I_{C2}=I_O
\end{equation}$$
电阻R上的电流为
$$\begin{equation}
I_R=\frac{V_{CC}-V_{BE1}}{R}=I_{C1}+\frac{I_{C1}}{\beta}+\frac{I_{C2}}{\beta}=I_O(1+\frac{2}{\beta})
\end{equation}$$
当晶体管的交流放大系数$\beta$很大时,有
$$\begin{equation}
I_R=I_O(1+\frac{2}{\beta})=I_O
\end{equation}$$
即输出电流与参考电流成镜像关系,所以该电路又称电流镜,输出电流的大小可通过电阻R来确定
$I_O$与$I_R$失配不但与晶体管的交流放大系数有关,而且也受基区宽度调变效应的影响.此时双极晶体管两管的C、E压降不同.回顾一下基区宽度调变效应下的集电极电流表达式为
$$\begin{equation}
I_C=I_Se^{\frac{V_{BE}}{V_t}}(1+\frac{V_{CE}}{V_A})
\end{equation}$$
电流源的输出阻抗是从$T_2$的集电极视入的阻抗,$T_2$是共射组态,在忽略$h_{re}$时,它等于$r_{ce}$三观电流源的结构如下所示,增加一个晶体管后可以减小共射交流放大系数造成的电流失陪
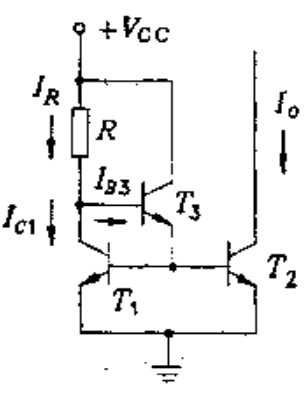
对此,我们可以得到如下方程式
$$\begin{equation}
I_{E3}=\frac{I_{C1}}{\beta}+\frac{I_{O}}{\beta}=2\frac{I_O}{\beta}
\end{equation}$$
$$\begin{equation}
I_{B3}=\frac{I_{E3}}{1+\beta}=\frac{2}{\beta(1+\beta)}I_O
\end{equation}$$
$$\begin{equation}
I_O=I_{C1}-I_{R}-I_{B3}
\end{equation}$$
可以得到
$$\begin{equation}
I_O=\frac{I_R}{[1+\frac{2}{\beta(1+\beta)}]}=\frac{I_R}{1+\frac{2}{\beta^2}}
\end{equation}$$
差动放大器
我们知道晶体管的直流工作点会随温度的变化而变化,各放大极的直流工作点将会互相影响,第一级的温度漂移是第二级输入信号的一部分,依此类推,致使在输入接地时,输出也将随时间变化,这种现象称为零点漂移.而降低零点漂移的常用方法是采用差动放大级
双极型差动放大器
双极型差动放大极的电路如下所示,其中两个晶体管是特性对称的对管
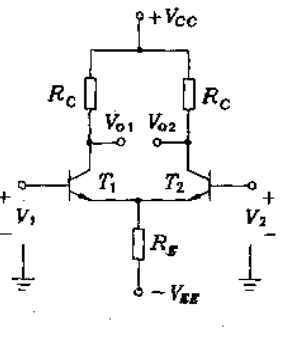
差动放大级有两个输入端,因此有两种输入信号,即差模信号和共模信号
如果两个信号的大小相等,极性相反,即$V_1=-V_2$,则是差模信号;
如果两个信号的大小相等,极性相同,即$V_1=V_2$,则是共模信号.
对于$V_1,V_2$为任意值的普遍情况,差模信号和共模信号的定义分别是
$$\begin{equation}
V_{ic}=\frac{V_1+V_2}{2}
\end{equation}$$
$$\begin{equation}
V_{id}=V_1-V_2
\end{equation}$$
由此可见,差模信号是二输入端之间的信号,共模信号是二输入端与地之间的信号.差模信号是有用的信号,共模信号往往是无用的信号大信号特性
在差动信号图中有
$$\begin{equation}
V_1=V_{BE1}-V_{BE2}+V_2
\end{equation}$$
根据大信号模型的集电极电流方程
$$\begin{equation}
I_C=I_Se^{\frac{V_{BE}}{V_t}}
\end{equation}$$
可以得到
$$\begin{equation}
V_{BE1}=V_t\ln\frac{I_{C1}}{I_{S1}}
\end{equation}$$
$$\begin{equation}
V_{BE2}=V_t\ln\frac{I_{C2}}{I_{S2}}
\end{equation}$$
注意到两个晶体管为同型晶体管,则$I_{S1}=I_{S2}$
由以上三式可以得到
$$\begin{equation}
\frac{I_{C1}}{I_{C2}}=\exp(\frac{V_1-V_2}{V_t})=\exp(\frac{V_{id}}{V_t})
\end{equation}$$
而
$$\begin{equation}
I_{C1}+I_{C2}=\alpha I_{EE}
\end{equation}$$
可以得到
$$\begin{equation}
I_{C1}=\frac{\alpha I_{EE}}{1+\exp(\frac{-V_{id}}{V_t})}
\end{equation}$$
$$\begin{equation}
I_{C1}=\frac{\alpha I_{EE}}{1+\exp(\frac{V_{id}}{V_t})}
\end{equation}$$小信号特性
差动放大级有两个输入端和两个输出端,因而有四种工作模式:单端输入-单端输出,单端输入-双端输出。双端输入-单端输出,双端输入-双端输出
差动放大级的交流特性可用半电路的方法,分纯差模输入和纯共模输入两种情况进行分析.前面我们已经说过任意信号都可以分解成纯差模信号和纯共模信号,因此任何情况都可以视为这两种情况的叠加.- 差模信号
对于纯差模输入信号,即$V_1=+\frac{V_{id}}{2}$,$V_2=-\frac{V_{id}}{2}$,差动放大级可以表示成如下图示,其中两个晶体管和负载电阻是对称的,一个管子电流增大,相应地,另一个管子的电流就会减小,且增量量值相等.因此E点电位不变,将电位不变的点接地,对电路的行为毫无影响.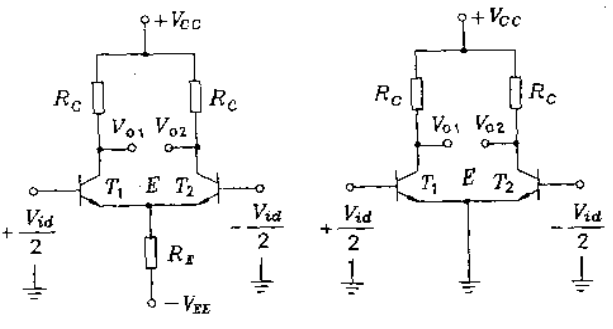
根据上图图示可以看出,纯差模信号电路是由两个半电路组成的,因此只需要分析其中一半即可.
$$\begin{equation}
V_{O1}=-\frac{\beta R_C}{r_{be}}\cdot\frac{V_{id}}{2}
\end{equation}$$
单端输出的电压增益为
$$\begin{equation}
A_d=\frac{V_{O1}}{V_1-V_2}=\frac{V_{O1}}{V_{id}}=-\frac{\beta R_C}{2r_{be}}≈-\frac{R_C}{2r_e}
\end{equation}$$
$$\begin{equation}\end{equation}$$
因为电路是对称的,所以$V_{O1}=-V_{O2}$,如果从双端输出,则双端输出的差模增益为
$$\begin{equation}
A=\frac{V_{O1}-V_{O2}}{V_1-V_2}=-\frac{\beta R_C}{r_{be}}≈-\frac{R_C}{r_e}
\end{equation}$$
定义二输入端之间的电阻$r_{id}$叫差模输入电阻
$$\begin{equation}
r_{id}=2[r_{b}+(1+\beta)r_{e}]
\end{equation}$$ - 共模信号
纯共模信号是指大小相等、极性相同的信号,即$V_1=V_2=V_{ic}$,出于电路对称性的考虑,我们将差模电路的电阻$R_E$分解成两个电阻的并联,得到如下图示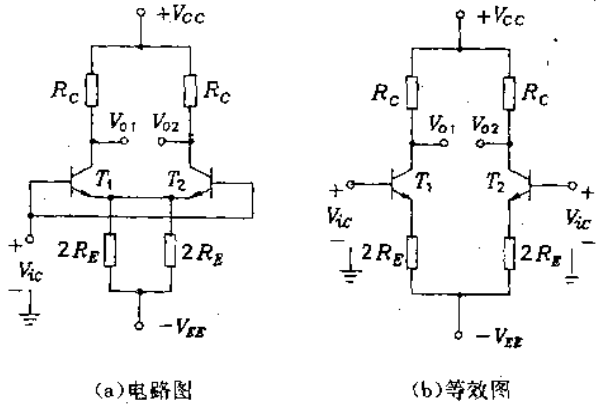
电路是对称的,则在加纯共模信号时,$\Delta I_{C1}=\Delta I_{C2}$,$T_1$和$T_2$的发射极电位相等,因而流过他们之间连线上的电流为零,故可以将他们断开.
由图可知
$$\begin{equation}
V_{O1}=-\frac{\beta R_C}{r_{be}+2(1+\beta)R_E}V_{ic}
\end{equation}$$
$$\begin{equation}
V_{O2}=-\frac{\beta R_{C}}{r_{be}+2(1+\beta)R_{E}}V_{ic}
\end{equation}$$
若是单端输出,则共模增益为
$$\begin{equation}
A=\frac{V_{O1}}{V_{ic}}=-\frac{\beta R_C}{r_{be}+2(1+\beta)R_E}≈-\frac{R_C}{2R_E}
\end{equation}$$
若从双端输出,则共模增益为
$$\begin{equation}
A=\frac{V_{O1}-V_{O2}}{V_{ic}}=0
\end{equation}$$
共模输入阻抗是自共模信号源视入的阻抗,即二输入端相联之后的对地阻抗
$$\begin{equation}
r_{ic}=[r_{be}+2(1+\beta)R_E]||[r_{be}+2(1+\beta)R_E]≈\beta R_E
\end{equation}$$
- 差模信号

This is an identification card as an honored membership of FeynmanDirac
Happy to see you follow FeynmanDirac, enjoy science together
 验证码启动中...
验证码启动中...
备用人机验证