Mechanical wave

机械振动在介质中的传播称为机械波（mechanical wave）。机械波与电磁波既有相似之处又有不同之处，机械波由机械振动产生，电磁波由电磁振荡产生；机械波的传播需要特定的介质，在不同介质中的传播速度也不同，在真空中根本不能传播，而电磁波（例如光波）可以在真空中传播；机械波可以是横波和纵波，但电磁波只能是横波；机械波与电磁波的许多物理性质，如：折射、反射等是一致的，描述它们的物理量也是相同的。常见的机械波有：水波、声波、地震波。

波动学

• 机械波：机械振动在弹性介质中的传播（常见的波都是属于这类），需要介质，如空气等。

• 简谐波：介质中各质元做简谐振动

• 非简谐波：介质中的各质元做非简谐运动

• 电磁波：交变电磁场在空间相互转换地传播，一般认为不需要介质

• 物质波：实物粒子产生的一种波动，主要表现在微观层面

机械波

产生条件：

• 弹性介质：可以看成无穷多个质元组成的，并且质元之间有弹性力的连续介质。（
• 波源：波源的质元开始振动并在弹性力地作用下把波源的振动状态向四周传递。

产生过程：

第一个质元开始振动带着第二个质元开始振动。一定注意是带着后面的质元一起振动，并不是第一个质元振动的时候跑到第二个质元的地方继续振动。==质元本身只是在原地振动,每一个质元都在前一个的带动下进行振动==，最后连在一起在宏观上就表现出波的感觉。

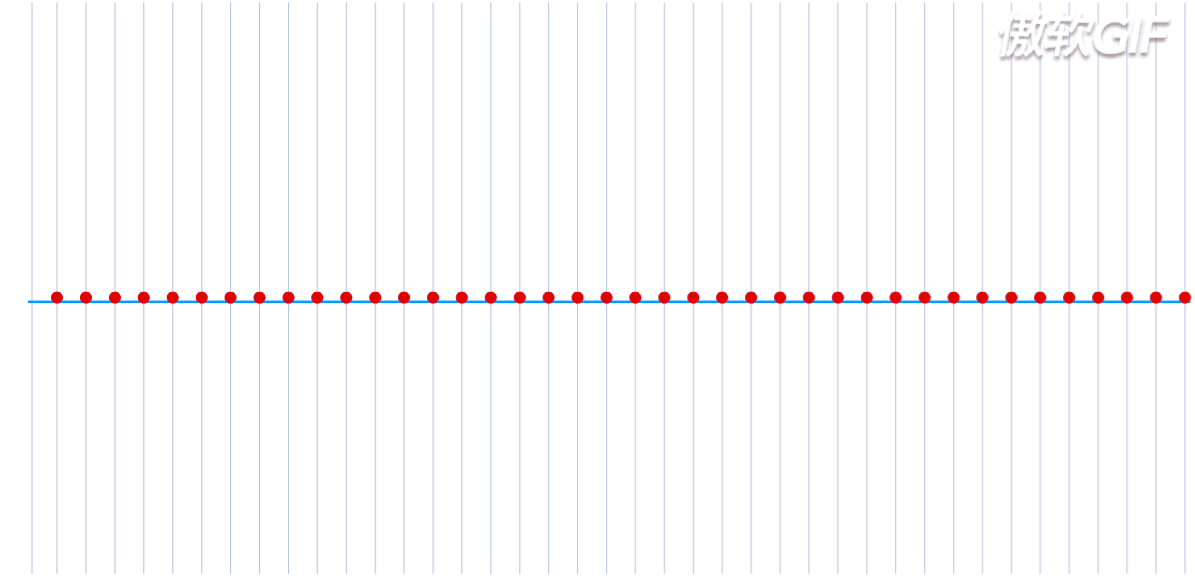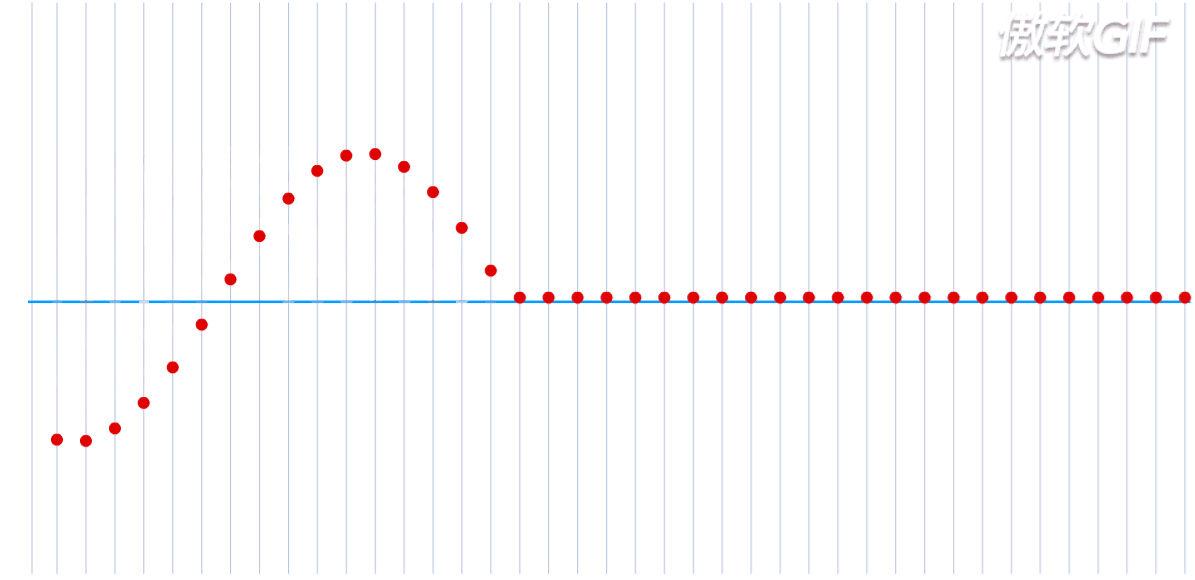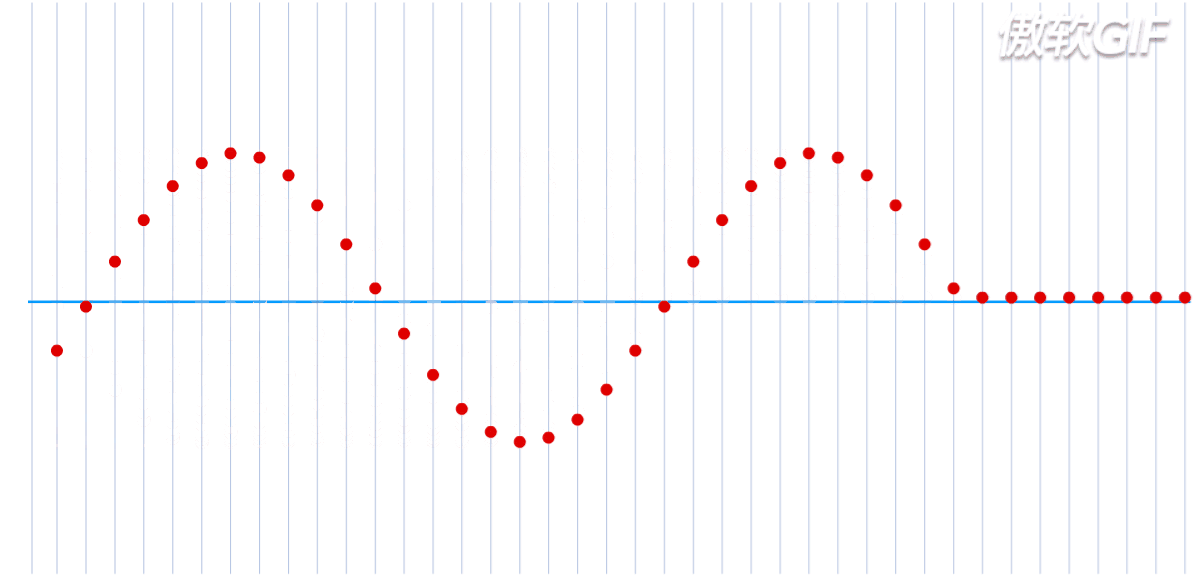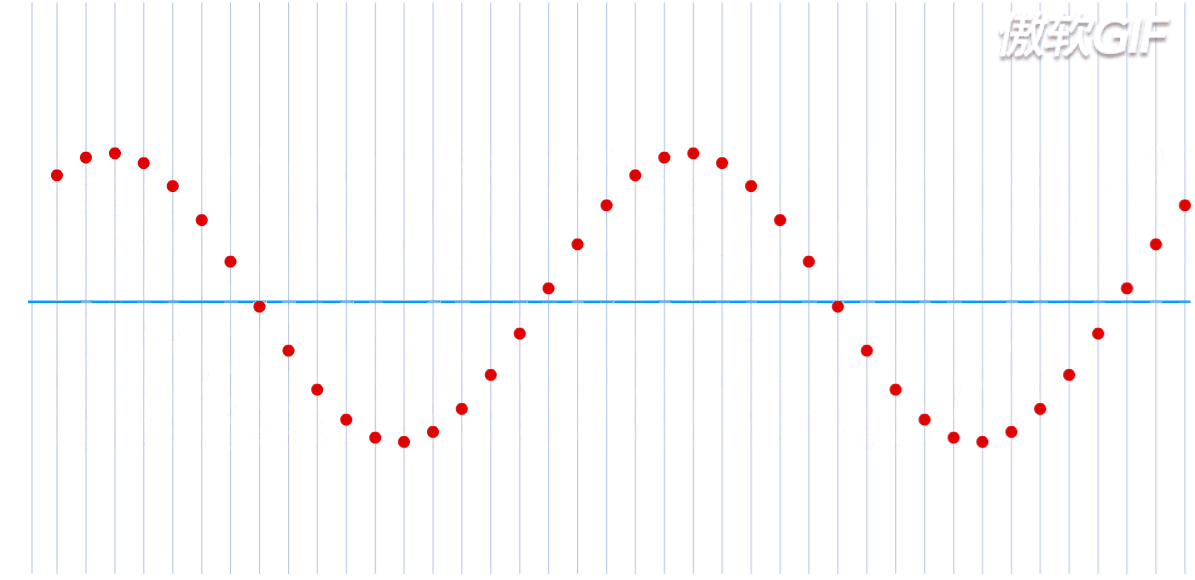
图中只展示了横波，也就是振动方向与波的传播方向垂直,而纵波就是振动方向与传播方向相同，如下: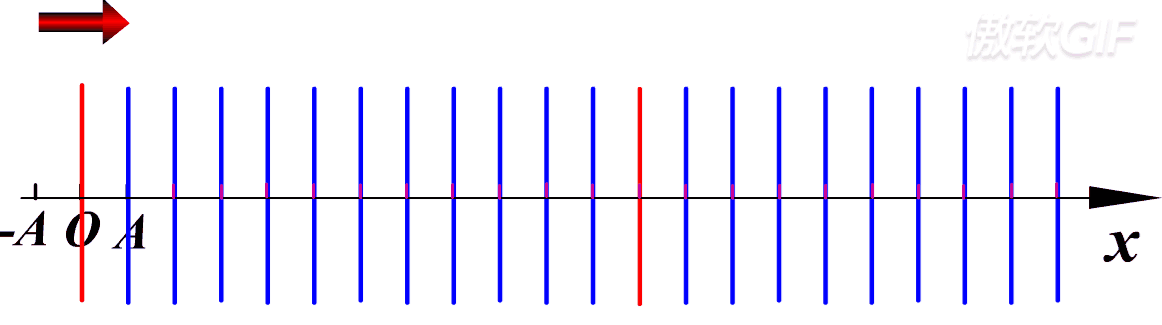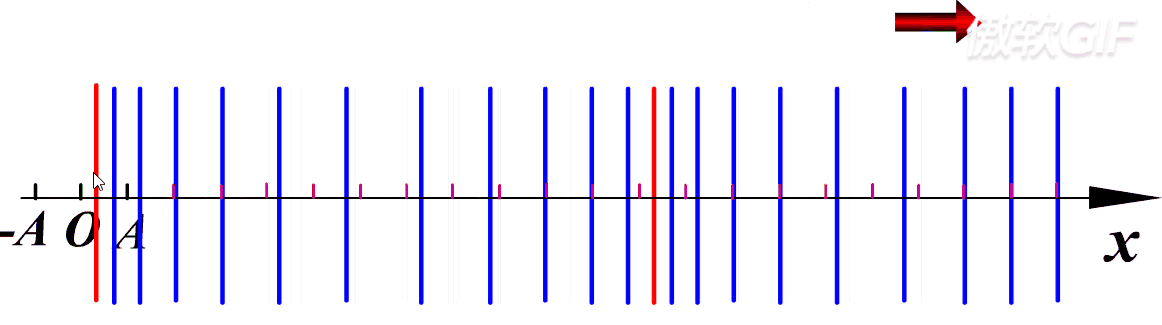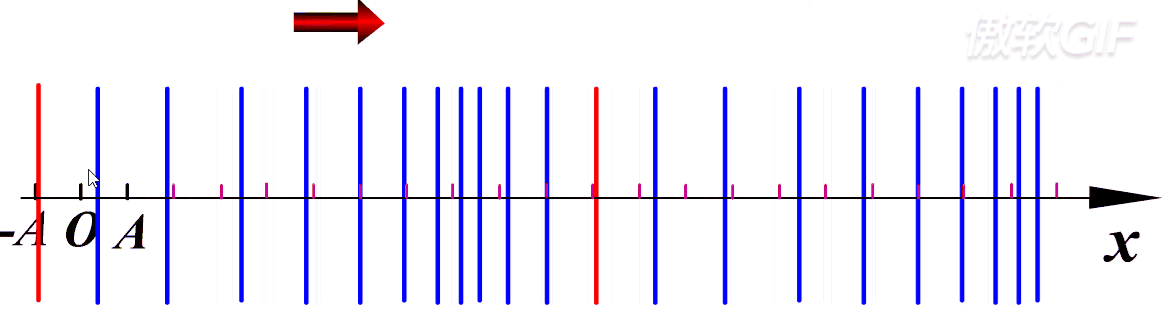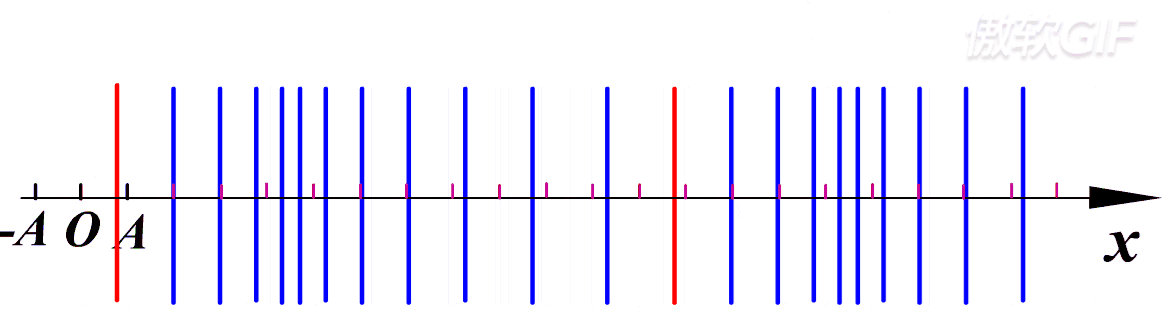

种类：

按照振动方式分类

• 横波：质元的振动方向与波的传播方向垂直，只有固体才能传递横波（因为你想你拿着固体的一角，你能够把固体提起来，但是你拿着气体或则液体的一角能把它提起来吗？很显然是不可以的，他们的分子之间没有垂直方向的回复力）
• 纵波：质元的振动方向与波的传播方向相同，固液气都可以传递纵波（利用横纵波的性质可以探测地壳，工业原件的裂纹等。缝隙中的空腔无法传递纵波。声波是纵波。）
• 横波纵波并不是两个冲突的分类。一个波可以是复合的，比如水波，就是既包含横波也包含纵波。

 按照传递方式分类

• 球面波：波面为球面的波称为球面波 ，就是由一点向四面八方传播。

• 平面波：波面为平面的波称为平面波，沿着一个方向传播。

一些基本术语：

• 波线：表示波的传播途径和方向的有向线段。

• 波面：振动相位相同的点所构成的面。

• 波阵面（波前）：在最前面的那个波面。

• 物理量：*

• $\lambda$ ：波长。同一波线上两个相邻的、相位差为2π的质点之间的距离。 也可以说在一个全振动周期内振动状态向前传播的距离。 $\lambda=\frac{u}{\nu}=Tu$

• $T$ ：周期。波前进一个波长的距离所需的时间。

• $\nu$ ：频率。单位时间内波动前进距离中完整波长的个数。（常用单位时间秒，对应频率单位就是赫兹） $\nu=\frac{1}{T}$

• $u$ ：波速。波动过程中，某一振动状态（即振动相位）单位时间内所传播的距离（相速）。 $u=\frac{\lambda}{T}=\lambda \nu$ （对于光 $c=\lambda\nu$ ）

• ==液体或气体中的纵波波速==： $u=\sqrt{\frac{B}{\rho}}$ （ $B$ 为容变弹性模量， $\rho$ 是密度）

• ==固体中的纵波波速==： $u=\sqrt{\frac{Y}{\rho}}$ （ $Y$ 是杨氏弹性模量， $\rho$ 是密度）

• ==固体中的横波波速==： $u=\sqrt{\frac{G}{\rho}}$ （ $G$ 是切变弹性模量， $\rho$ 是密度）

• ==绳索中的波速==： $u=\sqrt{\frac{F_{T}}{\rho_{l}}}$ （ $F_{T}$ 是张力， $\rho_{l}$ 是线密度）

（周期或频率只决定于波源的振动，简单来说等于波源振动的周期和频率。波速只取决于弹性介质的性质还有温度与振动状态无关，这一个性质决定了折射现象。）

平面简谐波

• 简谐波：在均匀的、无吸收的介质中，波源作简谐运动时，在介质中所形成的波。

• 方程：

• $y(x,t)=Acos[\omega(t-\frac{x}{u})+\varphi_{0}]$ （沿x轴正方向传播）。

• $y(x,t)=Acos[\omega(t+\frac{x}{u})+\varphi_{0}]$ （沿x轴负方向传播）。

• 一些其他表达形式（这里都是沿着x正方向传播的表达式）：

  1. $y(x,t)=Acos(\omega t-\frac{2 \pi x}{\lambda}+\varphi_{0})$
  2. $y(x,t)=Acos[2 \pi( \frac{t}{T}-\frac{x}{\lambda})+\varphi_{0}]$
  3. $y(x,t)=Acos[k( ut-x)+\varphi_{0}]$
     $k=\frac{2\pi}{\lambda}$ ，称之为波矢，表示在2π长度内所具有的完整波的数目

波动能量

单个质元的机械能

• $$\begin{aligned} dE=dE_{k}+dE_{p}=\rho A^{2}\omega^{2}sin^{2}[\omega(t-\frac{x}{u}) + \varphi_{0}]dV \end{aligned}$$
  在波动过程中，任一质元的动能和势能相等，且同相位变化

• 物理概念：

  1. 应变：弹性介质中，质元沿纵波传播方向受到相邻质元的内力（拉力或压力）作用而相应地发生伸长或压缩形变，其形变量与质元原有长度之比。简单来讲波本身是一个质元带动下一个质元运动，然后这个质元在来自相邻的质元的力发生形变。这个形变量与原来的长度比值就是应变。
  2. 应力：物体受外力作用而发生形变时，其内部会产生内力，此内力与作用而的面积之比称为应力。如内力沿作用面的法线方向，则称相应的应力为正应力。简单来讲就是所受力除以这个力的作用面积

• ==推导过程==：

• 动能部分，我们先把弹性介质分成无穷多份，那么每一份的体积是 $dV$ 。本身弹性介质的密度可以是不均匀，但是我们分成很多小份之后就可以看作是均匀的介质。那么每一个质元的质量就是:
  $$\begin{aligned}dm=\rho dV \end{aligned}$$
  每一点的运动方程是:
  $$\begin{aligned}y=A cos[\omega(t-\frac{x}{u}) + \varphi_{0}] \end{aligned}$$
  对t求偏导得到:
  $$\begin{aligned}v=\frac{\partial y}{\partial t}=-A\omega sin[\omega(t-\frac{x}{u}) + \varphi_{0}] \end{aligned}$$
  那么每一点的动能就是:
  $$\begin{aligned}dE_{k}=\frac{1}{2} \rho A^{2}\omega^{2}sin^{2}[\omega(t-\frac{x}{u}) + \varphi_{0}]dV \end{aligned}$$

• 势能部分,一个质元的应力就是 $\frac{dF}{dS}$ ，它的应变就: $\frac{dy}{dx}$
  而物体的应力与应变成正比，所以：
  $$\begin{aligned}\frac{dF}{dS}=Y\frac{dy}{dx}\end{aligned}$$
  又根据胡克定律，这个质元形变的方向是沿y轴，所以 $dF=kdy$ ,所以就可以求出 $k=Y\frac{dS}{dx}$ ，所以弹性势能：
  $$\begin{aligned}dE_{p}=\frac{1}{2}k(dy)^{2}=\frac{1}{2} \times \frac{YdS}{dx} \times (dx)^{2} \times (\frac{dy}{dx})^{2}\end{aligned}$$
  所以:
  $$\begin{aligned}dE_{p}=\frac{1}{2}YdV(\frac{dy}{dx})^{2}\end{aligned}$$
  而又因为y对x求偏导:
  $$\begin{aligned}\frac{\partial y}{\partial x} = -A\frac{\omega}{u}sin[\omega(t-\frac{x}{u}) + \varphi_{0}]\end{aligned}$$
  而波速与杨氏模量之间有:
  $$\begin{aligned}u=\sqrt{\frac{Y}{\rho}} \Rightarrow Y=\rho u^{2}\end{aligned}$$
  所以代入可得:
  $$\begin{aligned}dE_{p}=\frac{1}{2} \times \rho u^{2} \times A^{2}(\frac{\omega}{u})^2 sin^{2}[\omega(t-\frac{x}{u}) + \varphi_{0}] \times dV\end{aligned}$$
  化简就可以得到:
  $$\begin{aligned}dE_{p}=\frac{1}{2} \rho A^{2}\omega^{2}sin^{2}[\omega(t-\frac{x}{u}) + \varphi_{0}]dV\end{aligned}$$
  从上面的推导我们也不难看出动能和势能是相等的。

能量密度

• 单位体积的介质中波动的能量就是能量密度,其表达式为：
  $$\begin{aligned}w = \frac{dE}{dV}=\rho A^{2}\omega^{2}sin^{2}[\omega(t-\frac{x}{u}) + \varphi_{0}]\end{aligned}$$

• 平均能量密度：
  $$\begin{aligned}\bar{w} = \frac{1}{T}\int_{0}^{T}\rho A^{2}\omega^{2}sin^{2}[\omega(t-\frac{x}{u}) + \varphi_{0}] = \frac{1}{2}\rho A^{2}\omega^{2}\end{aligned}$$
  T是我们研究的直棒的长度,把每个单位体积的能量加起来求平均值就行了,如果不是直棒，就用dV来积分，如果密度不均衡还要对密度函数进行积分

• ==机械波的能量与振幅的平方、频率的平方以及介质的密度成正比==

• 能流： 单位时间内通过介质中某一面积的波动能量:
  $$\begin{aligned}P=w dx=\rho A^{2}\omega^{2}sin^{2}[\omega(t-\frac{x}{u}) + \varphi_{0}]dx\end{aligned}$$

• 平均能流（波的功率）： 单位时间内垂直通过介质中某一面积的平均能量:
  $$\begin{aligned}\bar{P} = \frac{\bar{w}dV}{dt} = \frac{\bar{w}Sudt}{dt}=\frac{1}{2}\rho A^{2}\omega^{2}uS\end{aligned}$$
  其中S是横截面积

• 能流密度（波的强度）： 垂直通过单位面积的平均能流。注意如果截取平面不与波的传递方向垂直，要考虑有效的投影面积是什么，单位 ： $W/m^{2}$ （单位面积的功率）：
  $$\begin{aligned}I=\frac{\bar{P}}{S}=\frac{1}{2}\rho A^{2}\omega^{2}u\end{aligned}$$

• 当取矢量表达式的时候，方向与波速方向相同。

波的吸收

• 振幅的关系： $A=A_{0}e^{-\alpha x}$ （ $A_{0}$ 最初的振幅， $x$ 到波源的距离， $\alpha$ 吸收系数满足 $-dA=\alpha A dx$ ）
• 波强（能流密度）的关系： $I=I_{0}e^{-2\alpha x}$ 。
• 推导过程：在地球上大部分情况波在传递过程中都会被吸收，它的能量会不断减少。只要知道了 $-dA=\alpha A dx$ ，当前的振幅与距离和振幅的乘积成比例就行了。这就是个解微分方程的过程。 $\alpha$ 就是吸收系数， $\alpha$ 越大肯定衰减的越快，越小衰减的越慢。

声

分类：

• 声波：频率在20 Hz ~ 20 000 Hz波段的机械波

• 超声波：频率高于20 000 Hz 的声波

  1. 频率高，声强大
  2. 定向传播性能很好
  3. 遇障碍物时易形成反射
  4. 在水等一些介质中的衰减系数较小，穿透本领好

• 次声波：频率低于20 Hz 的声波

  1. 频率低、波长甚长
  2. 衰减极小

• 声压：*

• 某一时刻，在介质中的某处，有声波传播时的压强 $p$ 与无声波传播时的压强 $p_{0}$ 之差:
  $$\begin{aligned}p=-\rho A \omega u sin[\omega (t-\frac{x}{u})+\varphi_{0}] = \rho u v\end{aligned}$$
  （ $u$ 声速， $v=-A \omega sin[\omega (t-\frac{x}{u})+\varphi_{0}]$ ，称为体积速度）。

• 声压随空间位置和时间作周期性变化，并且与振动速度同相位。

• 声阻抗： $Z=\rho u$ ，声波在两种不同介质分界面上反射和折射时的能量分配由该两种介质的声阻抗来决定。

• 声阻抗较大的介质称为波密介质

• 声阻抗较小的介质称为波疏介质

• 声压的幅值（最大值）： $p_{m}=\rho A \omega u$

• 声压与声强之间的关系： $I=\frac{1}{2} \frac{p_{m}^{2}}{\rho u}$

声强：

• 声波的能流密度:
  $$\begin{aligned}I=\frac{1}{2}\rho A^{2}\omega^{2}u\end{aligned}$$

• 声强级： $L=lg\frac{I}{I_{0}}$ 。（ $I_{0}$ 是个常数，称为标准声强，大小 $10^{-12} W\cdot m^{-2}$ ）。

• 单位：B（贝），1B（贝）=10dB（分贝）

• 反映了人类对于声音强弱的主观感觉

波的叠加原理

• 波传播的独立性：当几列波在空间某相遇后，各列波仍将保持其原有的频率、波长、振动方向等特征继续沿原来的传播方向前进 。
• 波的叠加原理 ：各列波在相遇区域内，任一质元的振动是各列波单独存在时对该质元所引起振动的合振动。

波的干涉

• 干涉：两列波在空间相遇（叠加），以致在空间的某些地方振动始终加强，而在空间的另一些地方振动始终减弱或完全消失的现象。

• 干涉条件：两列波的频率相同，振动方向相同，有恒定的相位差。在光学里红光和紫光肯定不能干涉，他们频率不相同。再如果都是红光，沿x轴传播，一个沿y轴振动，一个沿着z轴振动，那么振动方向不相同，肯定也不能干涉。

• 相干波源：能产生相干波的波源。

• 结论： $\Delta\varphi=\varphi_{2}-\varphi_{2}-\frac{2\pi}{\lambda}(r_{2}-r_{1})$ 。

  1. $\Delta\varphi=2k\pi+\pi$ ， $（k\in Z）$ 。则这个点的波是相互抵消为零（光学中的暗纹）。
  2. $\Delta\varphi=2k\pi$ ， $（k\in Z）$ 。则这个点的波是最大的相互叠加（光学中的亮纹）。

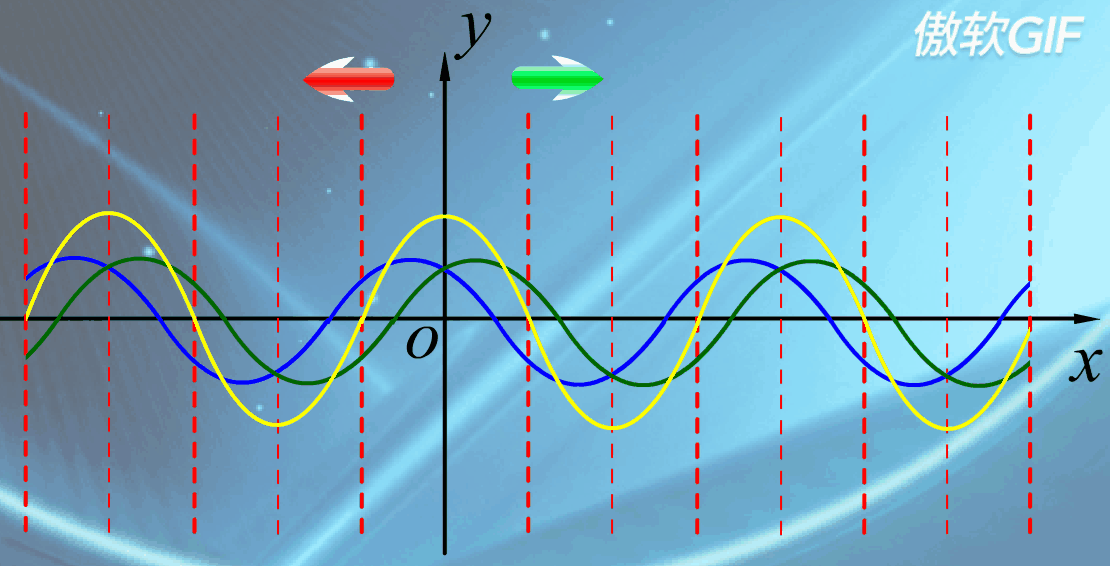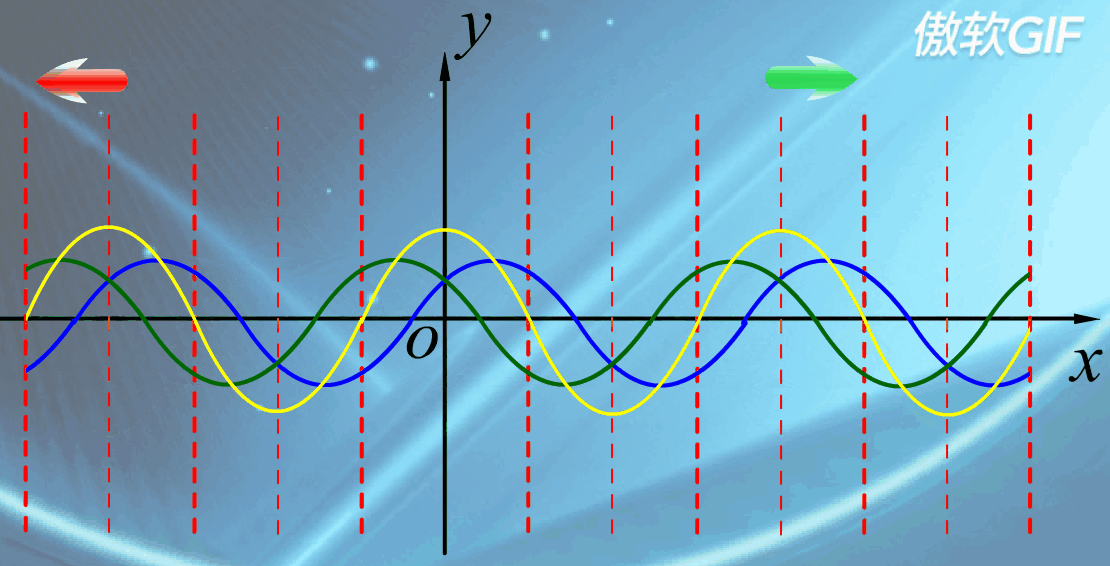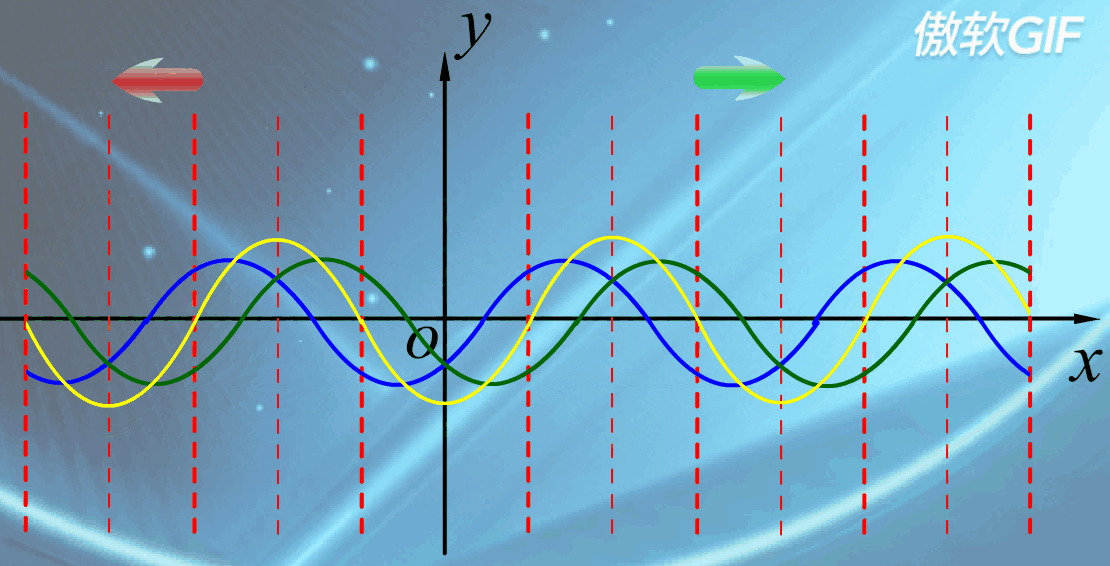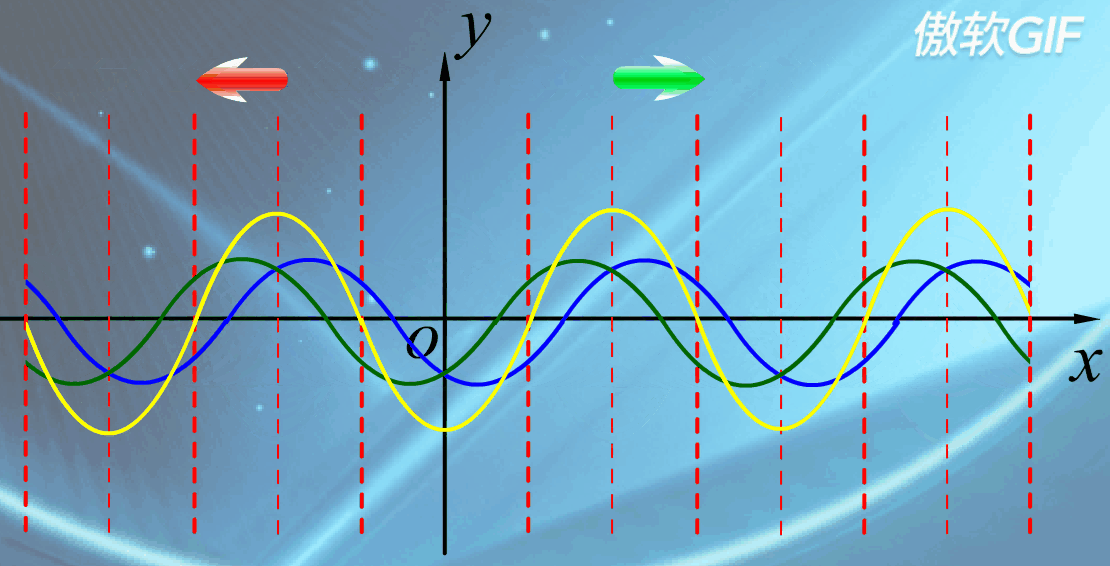
驻波

驻波的特点与方程

• 驻波的方程： $y=y_{1}+y_{2}=2Acos(2\pi \frac{x}{\lambda}) \times cos(\omega t)$

• 在x点的振幅： $\left| 2Acos(2\pi \frac{x}{\lambda}) \right|$ 。

• 波腹： 质元的振幅最大，为 $2A$ 的点。以坐标原点为波腹，则每个波腹的坐标 $x_{k}=2k\frac{\lambda}{4}=\frac{k\lambda}{2}$ 。两个相邻的波腹，振动始终相反，差 $\pi$ 的相位。

• 波节： 质元的振幅为零的点。以坐标原点为波腹，则每个波节的坐标 $x_{k}=(2k+1)\frac{\lambda}{4}=\frac{k\lambda}{2}+\frac{\lambda}{4}$

• 每一个质元都在做自己简谐运动，没有传递能量。

• 相邻波节（波腹）的距离 $\frac{\lambda}{2}$

• 驻波的特点：

  1. 没有波形的推进，也没有能量的传播，参与波动的各个质点处于稳定的振动状态。
  2. 各振动质点的振幅各不相同，但却保持不变，有些点振幅始终最大，有些点振幅始终为零。

驻波产生的条件

• 振幅、频率、传播速度都相同的两列相干波，在同一直线上沿相反方向传播时叠加而形成的一种特殊的干涉现象。
  

驻波的能量

• 驻波能量以形变势能的形式主要集中于波节附近。驻波能量以动能的形式主要集中于波腹附近。驻波中的动能和势能在波腹和波节间的小范围内迁移并转换。驻波进行过程中没有能量的定向传播。

• 动能的能量密度： $w_{k}=2\rho A^{2}\omega^{2}cos^{2}(2\pi \frac{x}{\lambda})sin^{2}(\omega t)$

• 势能的能量密度： $w_{p}=2\rho A^{2}\omega^{2}sin^{2}(2\pi \frac{x}{\lambda})cos^{2}(\omega t)$

半波损失

• ==机械波和电磁波都有这个性质==

• 波阻： $Z=\rho u$ （ $\rho$ 介质的密度， $u$ 波在介质中传播的速度）

• 相对波阻：

• 波密： 比较的介质中，相对波阻较大的介质称为波密介质。

• 波疏： 比较的介质中，相对波阻较小的介质称为波疏介质。

• 在垂直入射和掠射的情况下，当波由波疏介质射入波密介质发生反射的时候，就会发生半波损失。 也就是在这一个非常接近交界面的点的位置，振动的相位是 $\varphi$ ，前进那么很微小的距离，接触了交界面反射回来，它的相位就会增加半个周期，变成 $\varphi+\pi$

• 在垂直入射的情况下，它由介质的相对波阻Z决定。当波从波疏介质入射到波密介质时，反射有半波损失（相位差为π），反射点为波节；反之，当波由波密介质入射到波疏介质时，反射无半波损失，反射点处为波腹。

• 因为反射回来的波，肯定和波本身振幅、频率、传播速度都相同。那么这两列波如果相遇就一定能形成驻波。

惠更斯原理

• 惠更斯原理：某一时刻，同一波面上的各点，都可以看做是发射子波的波源，在其后的任一时刻，这些子波波源发出的子波波面的包络面就是该时刻的新波面。 简单来说就是，波的任何一点都可以看作是一个波源

波的衍射

• 波的衍射现象：波在传播过程中遇障碍物、小孔时，能绕过障碍物或则穿过小孔继续传播的现象。小孔或障碍物的尺寸与波长差不多，或比波长更小时。

• 光也是一种波，可见光的波长在380-780纳米。细胞的大小在1微米-几厘米不等。所以光学显微镜可以看见细胞。但是病毒的大小一般在18纳米~450纳米，与可见光的波长差不多，这时候再用光学显微镜就无法看见病毒，光就会绕过病毒继续传播。

波的反射与折射

• 定义： 波传播到两种介质的界面时，一列波被分成两部分，一部分反射回来，形成反射波，另一部分进入另一种介质，形成折射波，这种现象称为波的反射与折射现象。
• 反射定理：入射角等于反射角。
• 折射定理： $\frac{sin i}{sin \gamma}=\frac{u_{1}}{u_{2}}=n_{21}$ （ $i$ 入射角， $\gamma$ 折射角。 $u_{1}$ 波在第一个介质中的传播速度。 $u_{2}$ 波在第二个介质中的传播速度。 $n_{21}$ 第二种介质相对于第一种介质的相对折射率）