Rigid body mechanics

刚体动力学是力学的一个分支，研究刚体在外力作用下的运动规律。它是计算机器部件的运动，舰船、飞机、火箭等航行器的运动以及天体姿态运动的力学基础。

刚体的定义：

_在任何外力的作用下不发生形变的物体_。刚体是理想化的物体。并且可视为由无限多个彼此间距离保持不变的质元组成的质点系。

刚体的运动：

平动：刚体在运动过程中，其上任意两点的连线始终保持平行。（平动没有什么好说的，就可以当做一个质点来进行计算，基本上大家利用高中所学的知识就能够完成平动的计算）

转动：刚体上所有质点都绕同一直线做圆周运动。这种运动称为刚体的转动。这条直线称为转轴。（这部分才是刚体力学的重点，下面的部分讲的就是刚体的转动部分）

接下来讲一下基本的物理量：

$\theta$ ：角度（ $\Delta\theta$ ：在某个时间内转过的角度）

$\omega$ ：角速度（假设角度随时间变化的方程是 $\theta(t)$ ，则 $\omega=\frac{d\theta}{dt}$ 就是其对时间的求导）

$\alpha$ ：角加速度（ $\alpha=\frac{d^{2}\theta}{dt^{2}}$ ，对时间求二次导数）

角速度和角加速度均为矢量，定轴转动中其方向沿转轴的方向并满足右手螺旋法则

1.力矩： $M=r \times F\bot$ （注意这里是两个向量叉乘，我还不清楚知乎怎么打出向量的箭头符号）（这里的力是投影到刚体所在平面内的力，可以根据向量法则进行拆分出来）

大小： $M=r\times F\bot \times sin\theta$ ， $\theta$ 是两个向量的夹角

方向：满足右手螺旋法则

单位： $N\cdot m$

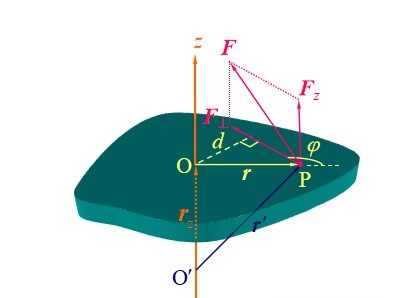
$F\bot$ 在平面内， $F_{z}$ 垂直于刚体所在平面， $F$ 是原本施加的力

2.角动量： $L=\omega\sum_{i=0}^{n}{m_{i} r_{i}^{2}}$

推导过程：因为我们知道平动的物体动量就是 $p=mv$ ，在转动过程中对于刚体中任意一质点的角动量 $L_{i}=m_{i}v_{i}r_{i}$ ，而我们又知道 $v=\omega r$ ，所以 $L_{i}=m_{i}\omega_{i}r_{i}^{2}$ ，而之前就讲过了，我们可以把刚体看成无穷多个质点。所以我们把所有的质点全部加起来就是整个刚体的角动量 $L_{i}=\sum_{i=0}^{n}{m_{i}\omega_{i}r_{i}^{2}}$ ，而同轴转动的物体，角速度相同。所以我们得到了公式： $L=\omega\sum_{i=0}^{n}{m_{i} r_{i}^{2}}$ 。

单位： $N\cdot m\cdot s$

注意事项：角动量是矢量（因为 $\omega$ 和 $r$ 是矢量，乘积出来也是矢量，因为$\omega$ 和 $r$夹角始终是 $\frac{\pi}{2}$ ，所以正弦值等于1对计算没有影响），方向满足右手螺旋法则。

转动惯量：

• $J=\sum_{i=0}^{n}{m_{i} r_{i}^{2}}$

联系：从式子我们就不难看出它与角动量之间的关系 $L_{z}=J_{z}\omega$ （这里的z是转动轴，绕z轴转动的意思）。

注意事项：

（1）.刚体的转动惯量与刚体的形状、大小、质量的分布以及转轴的位置有关。 而与刚体的运动状态无关。

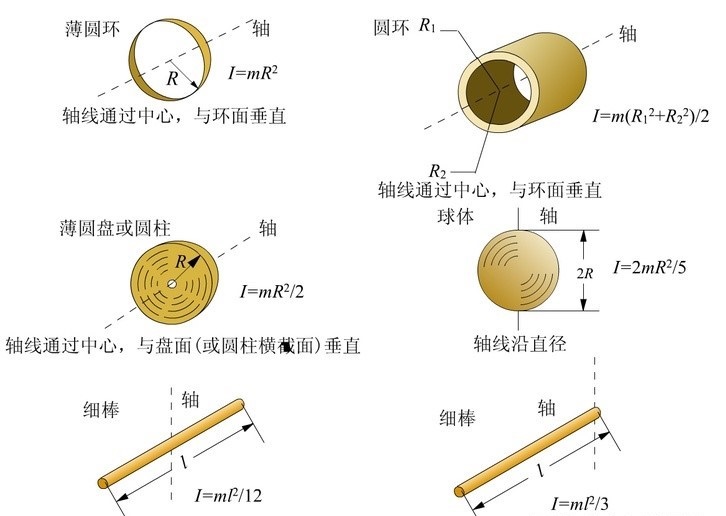
（2）.对于不规则的刚体，具体计算时可以采用积分等数学方法计算。对于常见的形状，建议大家还是记住其转动惯量是多少。

巧算方法：若刚体对一个过质心的轴的转动惯量为 $J_{c}$ ，则刚体对与该轴相距为 $d$ 的平行轴z的转动惯量 $J_{z}$ 是 $J_{z}=J_{c}+md^{2}$ 。这个式子极为重要！！而且一定要记住 $J_{c}$ 的轴一定要过质心。

常见物体转动惯量：

转动定理：

刚体在做定轴转动时，刚体的角加速度与它所受到的合外力矩成正比，与刚体的转动惯量成反比。 $M=J\alpha$ （力矩=转动惯量*角加速度）（在平动之中 $F=ma$ ，是不是感觉很相似呢）

推导过程： $J\alpha=\alpha\sum_{i=0}^{n}{m_{i} r_{i}^{2}}=\sum_{i=0}^{n}{\alpha m_{i} r_{i}^{2}}=\sum_{i=0}^{n}{F r_{i}}=M$ （这里的M是合力矩）

角动量守恒定理：

在平动中就讲了动量守恒，在所受合外力为0，或则内力远远大于合外力的时候物体的动量是保持守恒的。在刚体转动过程中也有这样子的性质，当刚体所受合外力的力矩为0的时候，也就是 $M=0$ 时， $L=J\omega$ 将会保持衡量，不会变化。（该定律不但适用于刚体，同样也适用于绕定轴转动的任意物体系统。 ）

$M=0$ 的几种情况：

（1）合外力 $F$ 投影下来的 $F_{\bot}$ 为0。

（2）$F_{\bot}$ 与转动半径 $r$ 的夹角为0°。

推导过程：上次就讲了 $M=J\alpha$ 、 $L=J\omega$ ，而 $\alpha=\frac{d\omega}{dt}$ 。所以 $M=\frac{dL}{dt}$ 。所以 $\int_{t_{1}}^{t_{2}}Mdt=L_{t2}-L_{t1}$ 。当 $M=0$ 时， $\Delta L=0$ 。所以角动量守恒。书上的原话就是：在某一时间段内，作用在刚体上的外力的冲量矩等于刚体的角动量增量。（力矩对时间的积分就是冲量矩，角动量变化量就是角动量的增量）

角动量守恒的常见情况：

（1）转动惯量改变
假设人是一个圆柱（理想化一下），双臂张开的转动惯量 $J_{1}$ 肯定大于双臂收拢的转动惯量 $J_{2}$ ，在没有外力的情况下，一定会有 $\omega_{1}<\omega_{2}$ 。

（2）平动物体撞上刚体

1.力矩对刚体所做功的功率

公式：$P=M\omega$

单位：W

推导过程：对于合外力在极小的 $\Delta t$ 时间内所做的功，一定可以表示为： $dW=F \cdot ds=F \cdot sin\varphi \cdot rd\theta$ （高中数学公式： $ds=r \cdot d\theta$ 。又是两个向量相乘，所以要带上 $sin\varphi$ ）

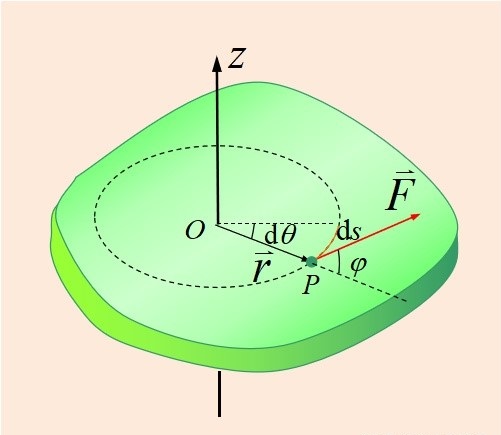
而又因为 $M=Fr \cdot sin\varphi$ ，所以 $dW=Md\theta$ 。所以 $P=\frac{dW}{dt}=M\frac{d\theta}{dt}=M\omega$

2.力矩对刚体所做的功

公式： $W=\int_{0}^{\theta}Md\theta$

单位：J

推导过程：上面讲功率已经推到了 $dW$ 。所以积分一下就可以了。

刚体转动的动能

公式： $E_{k}=\frac{1}{2} J \omega^{2}$

单位：J

推导过程： $dW=Md\theta$ ，而 $M=J\alpha=J\frac{d\omega}{dt}$ 。所以两式联立，得 $dW=J\frac{d\omega}{dt} d\theta=J\frac{d\theta}{dt} d\omega=J\omega d\omega$ 。所以动能 $E_{k}=\int_{0}^{\omega}dW=J\int_{0}^{\omega}\omega d\omega=\frac{1}{2}J\omega^{2}$

常见几种模型的各个量是否守恒：

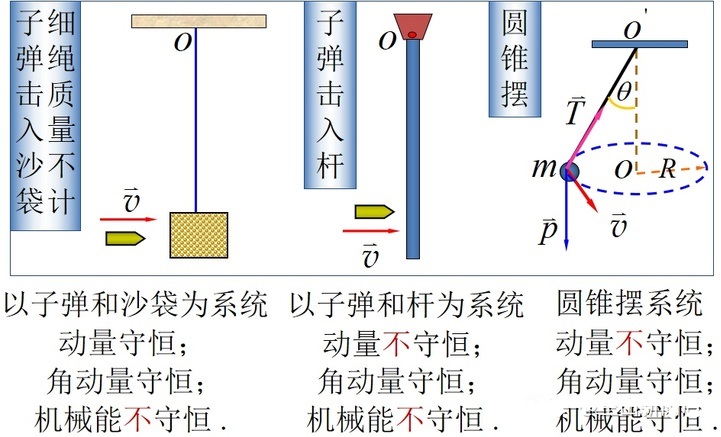
刚体的重力势能

公式： $E_{p}=mgh_{c}$ （ $h_{c}$ 是刚体质心到零势面的高度）

单位：J

刚体的机械能守恒

公式： $E=E_{p}+E_{k}$

应用：如图，质量为m，长为l的均匀细棒绕过O点的转轴自水平位置以零角速度自由下摆。求细棒运动到与水平夹角为 $\theta$ 时的角速度；

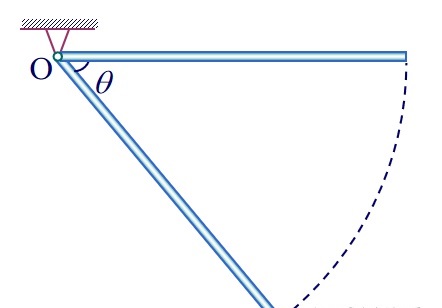
解：根据能量守恒，重力势能减小量是 $\Delta E_{p}=mg\cdot \frac{1}{2}l\cdot sin\theta$ 。动力势能增量是 $\Delta E_{k}=\frac{1}{2}J\omega^{2}$ 。而根据上次讲的，易知 $J=\frac{1}{3}ml^{2}$ 。所以： $\Delta E_{p}=\Delta E_{k}$ 。解方程： $mg\cdot \frac{1}{2}l\cdot sin\theta = \frac{1}{6}ml^{2}\omega^{2} \Rightarrow \omega^{2}=\frac{3g sin\theta}{l} \Rightarrow \omega=\sqrt{\frac{3g sin\theta}{l}}$

在前面研究公式的时候，我们就发现了许多平动与刚体转动公式之间的惊人的相似 。就好像被人刻意设计过一样。下面把两边的公式总结并且类比一下。