双折射

晶体双折射现象的基本规律

• 非晶体
  如玻璃、熔融石英等，一般不具有长程有序的内在结构，并且由于其原子或分子的热运动以及在空间排列上的随机性，其光学性质一般在宏观上呈现出各向同性

• 晶体
  具有内在结构长程有序的固体，其原子(离子或分子)在空间上排列具有一定的规则性，胜场良好的单晶体具有规则的几何外形

  • 除立方晶系的单晶体具有空间各向同性的光学性质外，一般的单晶体的光学性质均具有空间上的各向异性
  • 在一定的外界物理场作用下，某些非晶态介质甚至立方晶晶体会在宏观上由各向同性转变为各向异性.这种场致各向异性与晶体的自然各向异性具有类似的特点

• 最常见的两种各向异性晶体就是方解石和石英

  双折射

• 双折射就是同一束入射光同时出现两个偏折方向的现象

• 由于双折射，一束自然光通过某种各向异性晶体制成的平行平板后，将分解成两束相互错开但方向平行的透射光波，导致出现互相错开的双重折射影像.当以入射光线为轴线旋转该介质平板时，至少有一束透射光或一个影像的位置会随之旋转，两束透射光波或两个重叠的折射影像均表现为平面偏振特性，且振动方向正交

• 折射定律一般仅适用于各向同性介质，对于各向异性晶体，一般情况下，由双折射产生的两束折射光波中至少有一束不满足折射定律。入射光方向不同，晶体结构及空间取向不同，则双折射性质不同

• 一些概念

  • ①o光与e光
    寻常光(o光)：晶体中始终满足折射定律的光束，o光是光矢量与o光主平面垂直的线偏振光
    非常光(e光)：晶体中一般不满足折射定律的光，e光是光矢量与e光主平面平行的线偏振光
  • ②光轴
    光轴：晶体中存在一些特定方向，沿此方向入射的自然光不发生双折射现象
    单轴晶体：只有一个光轴的晶体，如方解石、石英、铌酸锂、红宝石、金宝石等
    双轴晶体：包含两个光轴的晶体，如云母、黄玉、铌酸钾、蓝宝石等.自然界的晶体大多是双轴的
    晶体的光轴不是我们说的光学系统的光轴，晶体光轴仅仅表示了晶体中的一个特定方向，并非沿该方向上的特殊光线
  • ③晶体的主截面与主平面
    主截面：由晶体光轴与界面法线组成的平面
    主平面：由光轴及所考察光线组成的平面，分为o光主平面与e光主平面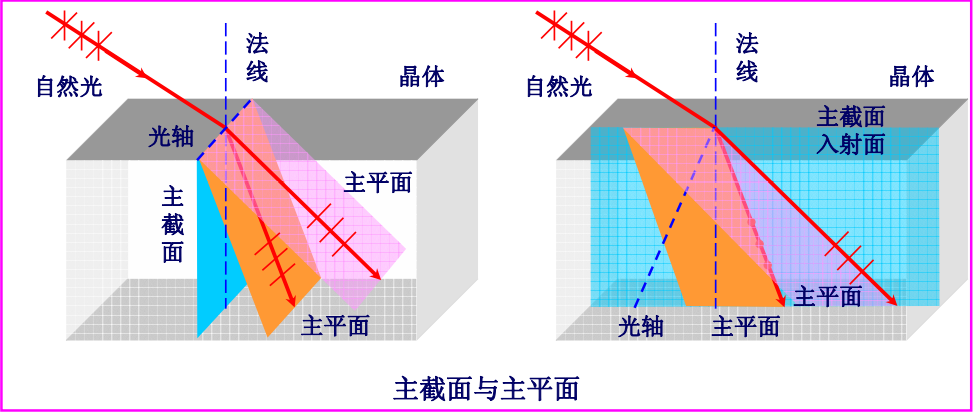
    
    主截面的方位由晶体自身特性决定，且始终垂直于晶体的表面
    主平面的方位则取决于光线及晶体光轴的取向，当主平面平行于入射面时，主截面也平行于入射面
    • o光光线始终位于入射面内，而振动平面垂直于o光主平面；e光光线可能不在入射面内，但其偏振面始终平行于e光主平面
    • 光轴位于入射面时，o光与e光主平面重合且与主截面重合，因而两折射光线的偏振面严格正交
    • 光轴不在入射面内时，o光与e光主平面严格讲不平行

      惠更斯对双折射现象的解释

• 惠更斯假设
  在单轴晶体中，o光子波的波面为球面，因而沿各个方向的传播速度相等;e子波的波面为旋转椭球面，因而沿各个方向的传播速度不相等;两个波面在晶体的光轴方向相切，因而任何子波沿光轴方向的传播速度相同，不发生双折射现象。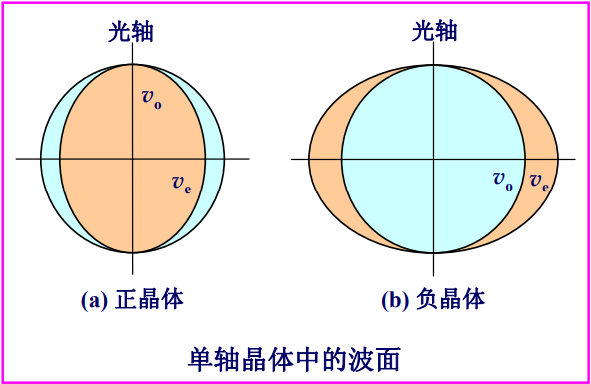
  

  沿光轴方向传播时，相应的子波速度为$v_o$:沿垂直于光轴方向传播时，相应的子波速度为$v_e$;对于沿任意方向传播的光波，相应的子波传播速度（设为v）介于$v_o$和$v_e$之间。
  正晶体:椭球的半长轴等于球面半径，$V_o$>$V_e$,$n_o$<$n_e$;
  负晶体:椭球的半短轴等于球面半径，$V_o<V_e$,$n_o>n_e$;

  寻常光的折射率与方向无关：$n_{o}$
  对于波矢量方向与光轴夹角为$\theta$的非常光，其折射率为
  $$\begin{aligned}
  n^2(\theta)=\frac{n_{o}^2n_{e}^2}{n_{e}^2\cos^2\theta+n_{o}^2\sin^2\theta}
  \end{aligned}$$

  单轴晶体中的光线方向

• 光轴平行入射面，并与界面呈一定角度
  
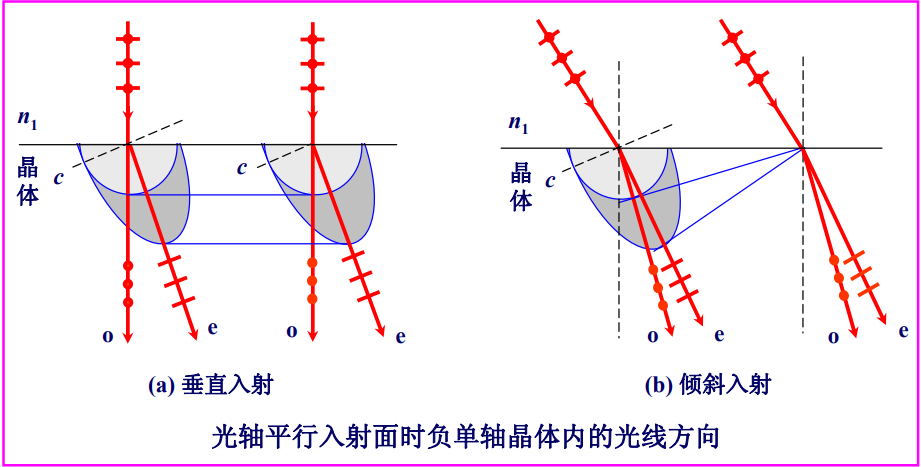
  无论是垂直入射还是斜入射，o光与e光分开，但因主截面与入射面重合，故o光主平面与e光主平面重合，e光仍位于入射面内.o光光线方向与波面正交，e光则不一定垂直于波面。

• 光轴同时平行于入射面和界面，平面波入射
  
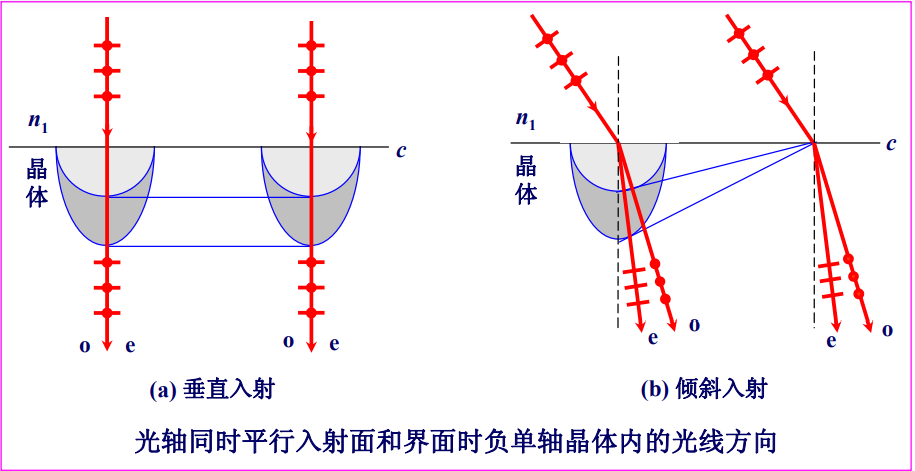
  主截面与入射面重合，故o光与e光主平面重合，振动方向正交。垂直入射时，o光与e光不分开，只是速度不同，分别为$v_o$和$v_e$.斜入射时，o光按$n_o$折射，e光按$n_e$折射，e光偏离o光，不满足折射定律

• 光轴平行于入射面，但与界面垂直，平行光入射
  
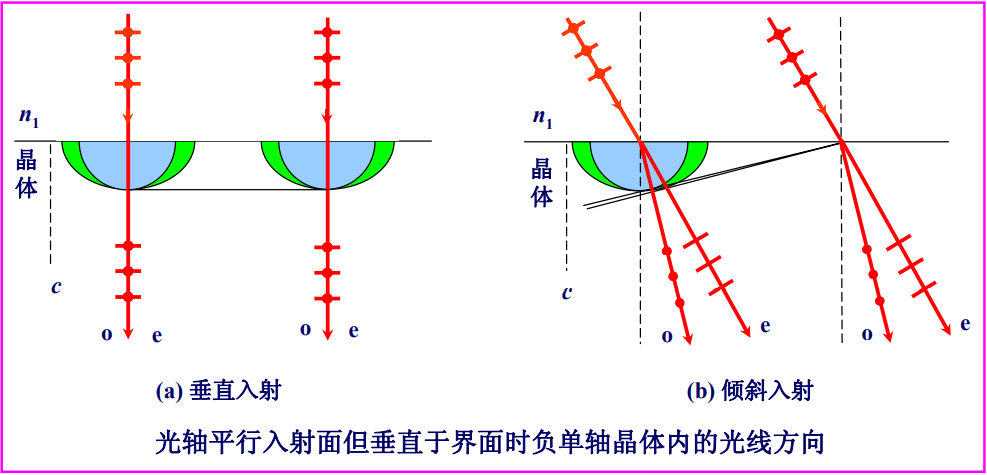
  o光和e光波面与入射面的交线分别为圆和椭圆，主平面、主截面与入射面重合，o光与e光振动方向正交。垂直入射时，o光与e光不分开，且速度均为$v_o$，斜入射时，o光与e光分开，e光不满足折射定律

• 光轴垂直于入射面，但与界面平行，平面波入射
  
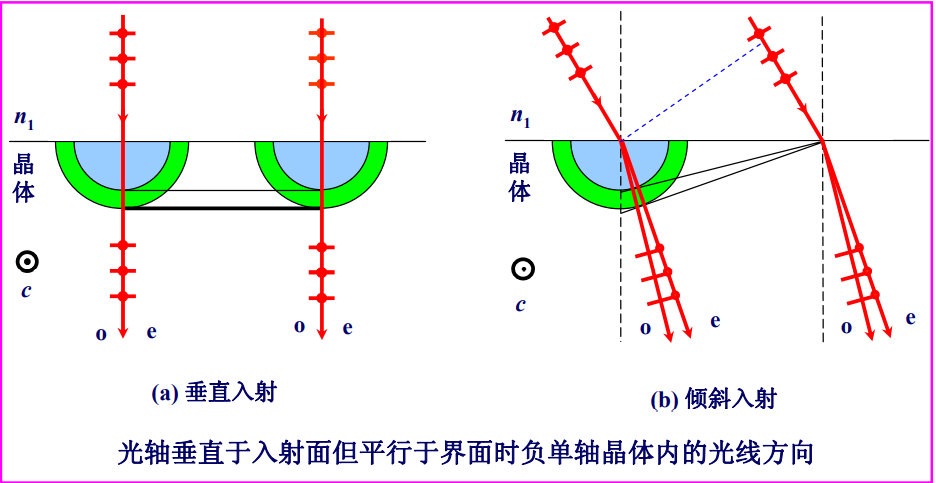
  o光和e光波面与入射面交线均为圆。主截面与入射面正交。垂直入射时，o光与e光不分开，仍按原方向行进，但速度不同，因而两束光产生的相位延迟不同，取决于各自的主折射率$n_o$和$n_e$。斜入射时，o光与e光因分别按$n_o$和$n_e$折射而分开，主平面不重合，但振动面正交

Reference
本文的参考文献如下¹

• [1]中国科学技术大学课件——光的双折射
• [2]中国科学技术大学课件——旋光现象

The end