本文将简要介绍几何光学中球面和透镜透镜组的成像

傍轴光线球面折射成像

单球面折射成像

• 轴上物点成像
  
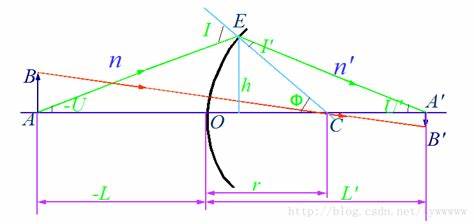
  参数:记AE = p,EA’ = p’,A0 = s,OA’ = s’,EC = r.
  推导：
  由正弦定理
  $$\begin{aligned}
  \frac{p}{\sin \varphi} = \frac{s + r}{\sin i};
  \frac{p’}{\sin \varphi} = \frac{s’ - r}{\sin i’}
  \end{aligned}$$
  由斯涅尔定律
  $$\begin{aligned}
  n \sin i =n’ \sin i’
  \end{aligned}$$
  可以得到
  $$\begin{aligned}
  \frac{p}{n(s+r)} = \frac{p’}{n’(s’-r)}
  \end{aligned}$$
  由余弦定理
  $$\begin{aligned}
  p^2 = (s+r)^2 + r^2 -2r(s+r)\cos \varphi;
  p’^2 = (s’-r)^2 + r^2 +2r(s’-r)\cos \varphi
  \end{aligned}$$
  由上述条件可以整理得到
  $$\begin{aligned}
  \frac{s^2}{n^2(s+r)^2} - \frac{s’^2}{n’^2(s’-r)^2} = -\sin^2 \frac{\varphi}{2}[\frac{4r}{n^2(s+r)} + \frac{4r}{n’^2(s’-r)}]
  \end{aligned}$$
  由上面的公式可以清晰地发现，同一物点所发出的光线方向不同时，折射后的光线与光轴的交点是不同的，即同心光束经球面折射后失去同心性.欲使得折射光线保持同心性，就需要使得像距s’仅仅是物距s的函数而与圆心角无关，下面做此讨论
  1. 等式右端为零
     当圆心角很小的时候，由数学极限可知右侧为零.这时上式可以化简为
     $$\begin{aligned}
     ±\frac{n(s+r)}{s} = ±\frac{n’(s’-r)}{s’}
     \end{aligned}$$
     这表明当圆心角很小时，物方光线和像方光线与光轴的夹角都很小，所有成像的光线都临近光轴，这种条件就是光线的傍轴条件(近轴条件)
     对于上图情况上式取正好，此时就得到单个球面折射的物像公式
     $$\begin{aligned}
     \frac{n}{s} + \frac{n’}{s’} =\frac{n’ - n}{r}
     \end{aligned}$$
     定义$\Phi$ = $\frac{n’ - n}{r}$为光焦度.光焦度的量纲是$m^{-1}，称作$屈光度(符号为D)
     当以平行光入射时，物距s为无穷大，根据公式就可以得到像方焦距f’
     $$\begin{aligned}s’ = \frac{n’}{n’ - n}r = f’\end{aligned}$$
     同样地当折射光线平行出射后，根据公式就可得物方焦距f
     $$\begin{aligned}
     s = \frac{n}{n’ - n}r
     \end{aligned}$$
     因此单球面折射的物像公式也可以表示为
     $$\begin{aligned}
     \frac{f}{s} + \frac{f’}{s’} = 1
     \end{aligned}$$
     上式称为高斯公式
  2. 等式两侧均为零
     为实现等式两侧均为零，只有满足透镜半径r无穷大时才能成立，这时就变成平面反射镜成像，这也是为什么之前我们描述过平面反射镜是唯一能够严格成像的光学仪器的原因

     轴外物点成像

  • 物所在的垂轴平面被称为物平面，像所在的垂轴平面被称为像平面
  • 由于实际物体总是存在一定高度的，因此实际发光点并不在主光轴上.根据上面推导的物像公式可以知道物距增大后像距必然要减小，因此实际成像图像将会是向球心弯曲的弧线，但这弧线并不是圆弧

    横向放大率

    将物和像的高度分别即为y、y’，我们定义像高与物高之比为像的横向放大率,用符号V表示
    $$\begin{aligned}V = \frac{y’}{y} = \frac{s’ \tan i’ }{s \tan i}\end{aligned}$$
    式中两个角度分别是与过光轴与镜面交点O的光线对光轴所成的入射和折射角度.由于满足傍轴条件，因此根据数学极限近似有tan(x) ≈ sin(x)
    因此横向放大率又可以表示为
    $$\begin{aligned}
    V = \frac{s’ \sin i’}{s \sin i} = \frac{ns’}{n’s}
    \end{aligned}$$

    焦平面

  • 过焦点并垂直于主光轴的平面称为焦平面
  • 与入射光线平行且通过球心的直线为次光轴

    几何光学的符号约定

  1. 当球心在像方时，球面的曲率半径r>0；当球心在物方时，球面的曲率半径r<0.
  2. 物或虚物在物方，物距s>0；物或虚武在像方，物距s<0.
  3. 像或虚像在像方，像距s’>0；像或虚像在物方，像距s’<0.
  4. 物(像)高度在主光轴以上取正，在主光轴一下取负.
  5. 角度自主光轴或法线算起，逆时针旋转为正，顺时针旋转为负.

傍轴光经球面反射成像

球面反射物像公式

• 根据球面折射的物像公式
  $$\begin{aligned}
  \frac{n}{s} + \frac{n’}{s’} = \frac{n’ - n}{r}
  \end{aligned}$$
  我们之前说过对于反射来说，其折射率n’ = -n并且角度i’ = -i.
  如果将反射看作是一种折射，那么用于折射的物像公式需要做出一些替代，将n’以-n替代，并且由于成像在物平面，因此像距s’将替代为-s’，即
  $$\begin{aligned}
  \frac{n}{s} + \frac{-n}{-s’} = \frac{-n-n}{r}
  \end{aligned}$$
  因此在反射中的物像公式为
  $$\begin{aligned}
  \frac{n}{s} + \frac{n}{s’} = \frac{-2n}{r} \Rightarrow \frac{1}{s} + \frac{1}{s’} = -\frac{2}{r}
  \end{aligned}$$
  此时球面镜的物方焦距和像方焦距相等且均为曲率半径负值的一半
  $$\begin{aligned}
  f = f’ = -\frac{r}{2}
  \end{aligned}$$
  当曲率半径为无穷大时就得到了平面镜反射成像的公式.

  球面镜成像的特点

• 横向放大率V
  $$\begin{aligned}
  V = \frac{y’}{y} = -\frac{ns’}{n’s} = -\frac{s’}{s}
  \end{aligned}$$
• 像的虚实与倒立
  根据球面镜反射成像的公式
  $$\begin{aligned}
  \frac{1}{s} + \frac{1}{s’} = -\frac{2}{r}
  \end{aligned}$$
  因此像距
  $$\begin{aligned}
  s’ = -\frac{sr}{2s+r}
  \end{aligned}$$
  对于球面镜反射来说，物距s总是正的，因此
  1. 当球面镜是凸面镜时，根据前面的几何光学符号规定，其曲率半径r>0，因此像距小于零，成像是虚像，且横向放大率V小于1，成像为正立缩小的虚像
  2. 当球面镜是凹面镜时，曲率半径r<0
     1. 当物距小于焦距时，成像像距小于零，为虚像，且横向放大率大于1，是正立放大的虚像
     2. 当物距大于焦距时，成像像距大于零，为实像，且横向放大率为负数，是倒立的实像

傍轴光线经薄透镜成像

• 所谓薄透镜，是指中心厚度比球面半径小得多且中心厚度也远小于物距和像距的透镜，这样可以近似认为两球面的顶点重合于透镜光轴的中心O，这一点就是薄透镜的光心

  薄透镜成像的物像公式

• 逐次成像法
  所谓逐次成像，即按序计算每一个光学系统的成像以得出最终的成像结果
  对于薄透镜我们做如下推导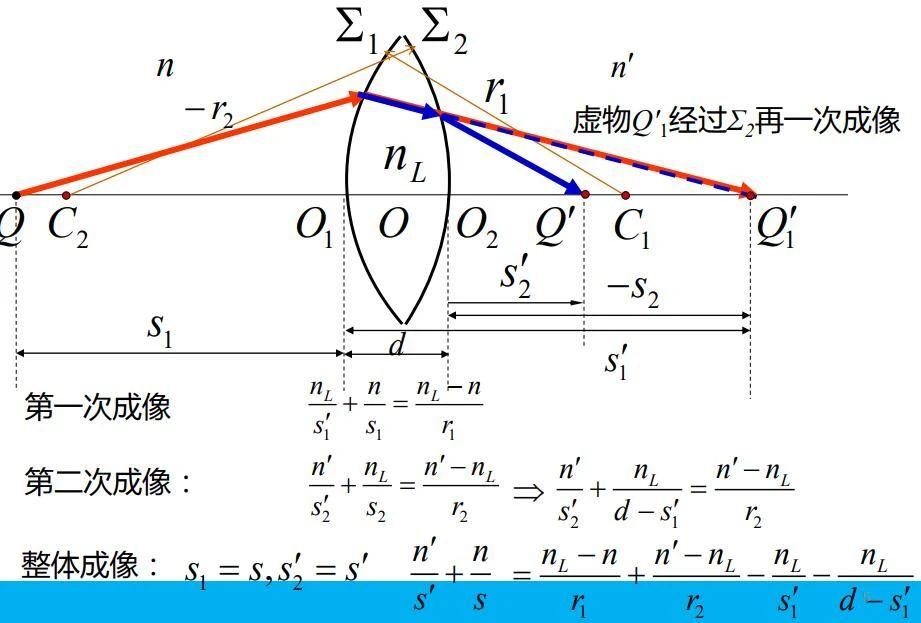
  
  1. 第一次成像，根据球面折射物像公式及相关符号规定
     $$\begin{aligned}
     \frac{n_1}{s_1} + \frac{n_L}{s_2} = \frac{n_L - n_1}{r_1}
     \end{aligned}$$
  2. 第二次成像的物实际上是第一次成的像，由于第二次成像的物处在像方平面，因此是虚物，根据符号规定其物距为负，虚物物距 = d - $s_2$≈$-s_2$
     $$\begin{aligned}
     \frac{n_L}{-s_2} + \frac{n_2}{s_3} = \frac{n_2 - n_L}{r_2}
     \end{aligned}$$
  3. 整合成像结果
     $$\begin{aligned}
     \frac{n_1}{s_1} + \frac{n_2}{s_3} =\frac{n_L - n_1}{r_1} +\frac{n_2 - n_L}{r_2}
     \end{aligned}$$
     根据光焦度的定义可知
     $$\begin{aligned}
     \Phi = \frac{n_L - n_1}{r_1} +\frac{n_2 - n_L}{r_2}
     \end{aligned}$$
     因此成像公式也可以表示为
     $$\begin{aligned}
     \frac{n_1}{s_1} + \frac{n_2}{s_3} = \Phi
     \end{aligned}$$
  4. 透镜的焦点
     • 物方焦距f
       $$\begin{aligned}
       f = \frac{n_1}{\Phi}
       \end{aligned}$$
     • 像方焦距f’
       $$\begin{aligned}
       f’ = \frac{n_2}{\Phi}
       \end{aligned}$$
  5. 磨镜者公式
     当光学透镜两端的介质均为空气时，其焦距
     $$\begin{aligned}
     f = f’ =\frac{1}{(n_L -1 )(\frac{1}{r_1} - \frac{1}{r_2})}
     \end{aligned}$$
  6. 薄透镜的高斯公式
     $$\begin{aligned}
     \frac{f}{s} + \frac{f’}{s’} = 1
     \end{aligned}$$
  7. 透镜分类
     在空气中，中间厚而两边薄的是汇聚的正透镜(凸透镜)，两边厚而中间薄的是发散的(负透镜)