Fundamental of geometrical optics
请注意,本文最近一次更新于:2022-03-12,文章内容可能已经不具有时效性,请谨慎参考
本文最后更新于:2022年3月12日星期六晚上6点18分 +08:00
本文将简要概述几何光学的基础知识
光线与几何光学的实验定律
- 光的直线传播定律
在均匀介质中,光沿直线传播 - 光的反射定律
反射光线在入射面内,反射角等于入射角 - 光的折射定律
当一束光线从一种介质进入另一种介质,光线的传播方向将发生改变.光线的折射满足斯涅尔定律.- 斯涅尔定律:
$$\begin{aligned}
n_1 \sin i_1 = n_2 \sin i_2
\end{aligned}$$
- 斯涅尔定律:
- 光路可逆原理
- 强调
上述实验定律并非在任何条件下都能适用,而是需要满足特定条件约束:- 光学系统的尺度远大于光波波长
- 介质是各向同性的
- 光强不是很大
费马原理
- 费马的表述
光沿着所需时间为极小值的路径传播 - 光程
光程等于折射率与光所经过的路程的乘积 - 费马原理
两点间光的实际路径是光程平稳的路径
特比需要说明的是。平稳的含义是光程可以取极值或者恒定值,数学上我们用变分表示为
$$\begin{aligned}
\delta(\overset{\frown}{P_1 P_2}) = \delta(\int_{P_1}^{P_2} n\mathrm{d}s) = 0
\end{aligned}$$- 强调
有些物理结论既不是建立在实验基础上的定律,也不是从数学上导出的定理,而是一个最基本的假设,是一切理论的出发点.一切定理和定律都建立在它的基础上,这就是原理.原理是一切理论体系的出发点.
费马原理不是定理,也不是定律,但它是几何光学的一个最基本的假设. - 由费马原理可以得出一个重要的结论,从一点发出的光线经过同一光学系统到达另外一点,各条光线都是等光程的,这就是物像之间的等光程性
- 强调
光的平面反射
- 假设平面反射镜前有一发光点A,我们知道从该发光点发出的光线经过平面反射镜反射后的光线是发散的,因此不能成像.但对观察者来说却能看到一个像B.根据反射定律我们明白AB是关于平面反射镜对称的两点.由于实际光线并没有穿过平面反射镜进入下方,因此B不是由实际光线汇聚而成的.因此B就是由虚光线形成的虚像,虚光线的光程称为虚光程
- 根据费马原理物像的等光程性,设平面反射镜上下册的折射率分别为n和$n\prime$,有
$$\begin{aligned}
n = - n\prime
\end{aligned}$$ - 在所有成像元件中,只有平面镜是能够严格精确成像的
光的平面折射
平面成像的傍轴条件
- 根据斯涅尔定律,不同入射角在介质表面折射的光线是发散的,他们的反向延长线并不汇聚于同一点,因此严格地讲平面折射是不能成像的.
- 尽管折射光线并不严格汇聚于同一点,但日常中我们能够看清折射后的成像,这是因为光线满足一定的条件.下面进行分析推导
- 设平静水面下深度为s处有一物点,取其中两条光线,一条垂直于界面出射,另一条光线与垂直出射的光线间距为L并与界面的入射角为i,折射角为$i\prime$.两条光线的反向延长线交点距离界面的距离为$s\prime$.根据折射定律及几何关系,可以得到
$$\begin{aligned}
s\prime = s\frac{\sin i}{\sin i\prime} \frac{\cos i\prime}{\cos i}
\end{aligned}$$
如果两条光线的发散角i不是很大,那么可得
$$\begin{aligned}s\prime = s\frac{\sin i}{\sin i\prime} = s\frac{n\prime}{n}\end{aligned}$$
若光线满足发散角较小,则称光线满足傍轴条件(近轴条件).满足傍轴条件的光线经过平面折射后可以成像.棱镜
- 设平静水面下深度为s处有一物点,取其中两条光线,一条垂直于界面出射,另一条光线与垂直出射的光线间距为L并与界面的入射角为i,折射角为$i\prime$.两条光线的反向延长线交点距离界面的距离为$s\prime$.根据折射定律及几何关系,可以得到
- 三棱镜是一种常用的折射器件,光从一侧射入并从另一侧射出的过程中发生了两次折射,出射光线相对于入射光线转过的角度称为偏转角
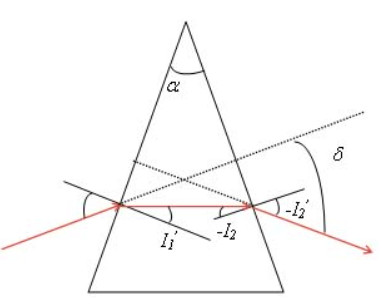
如上图所示,管线的偏转角$\delta = (I_1 - I_1\prime) + (I_2\prime - I_2)$,棱镜顶角$\alpha = I_1\prime + I_2$.
根据斯涅尔定律(这里取外界介质为空气,折射率取1,玻璃折射率为n)
由对称性以及数学分析可以证明当入射光与出射光对称,有最小的偏转角$\delta$,并根据折射定律可以得到:
$$\begin{aligned}
n = \frac{\sin i_1 }{\sin i_1 \prime} = \frac{\sin \frac{\alpha + \delta_{min}}{2}}{\sin \frac{\alpha}{2}}
\end{aligned}$$
通过测量三棱镜顶角和偏转角就可以得到棱镜材料的折射率.全反射
- 根据折射定律可知,当光线从光密介质射向光疏介质时,折射光线实际并不存在而只有反射光线,这种现象称为全反射.
根据折射定律可知全反射的临界角为:
$$i_c = \arcsin \frac{n_2}{n_1}$$霓虹现象
- 当空气非常洁净时,我们通常能在彩虹外围再看到一层与彩虹相似的图样,但我们可以其发现彩虹的颜色分布是相反的,我们称之为霓.
- 彩虹是外红内蓝而霓是内红外蓝的色彩分布
- 虹的成因是日光在水珠中发生折射、反射(或全反射),同时发生色散.从光学成像角度分析,虹是太阳的一个球差与色差的像
变折射率光学
变折射率介质
- 我们知道在两种不同的透明介质交界面处通过的光线会发生折射,但存在这样的一类透明介质,即使是在同一种介质中各处的折射率也不同。例如大气,由于受重力和温度的影响,在不同的环境、不同的高度,大气密度不同,因此折射率也不同。此外,由大气压强分布而引起的空气流动也会造成折射率的不同,但这种折射率是渐变的,因此渐变折射率的介质的折射率是空间位置的函数,印版可以表征为n = n(r),r是空间位矢.
光线方程
- 简化起见,这里我们假设空间折射率的变化只与高度有关,根据斯涅尔定律有
$$\begin{aligned} n_j \sin i_j = n_0 \sin i_0 ,j = 1,2,3… \end{aligned}$$
注意到
$$\begin{aligned} \frac{\mathrm{d}y}{\mathrm{d}x} = \cot i\end{aligned}$$
而
$$\begin{aligned}
\sin i = (\frac{1}{1 + \cot^2 i})^{\frac{1}{2}}
\ = (\frac{1}{1 + (\frac{\mathrm{d}y}{\mathrm{d}x})^2})
\ = \frac{n_0 \sin i_0}{n}
\end{aligned}$$
因此
$$\begin{aligned}
(\frac{\mathrm{d}y}{\mathrm{d}x})^2 = \frac{n^2 - n^2_0 \sin^2 i_0}{n^2_0 \sin^2_i0}
\end{aligned}$$
上述方程就是光线方程
您阅读这篇文章共花了:

Invitation
Floral-Sunsunrise
FeynmanDirac
created:12/03/2022
Welcome to Floral-Sunsunrise
This is an identification card as an honored membership of FeynmanDirac
Happy to see you follow FeynmanDirac, enjoy science together
© 版权声明
 验证码启动中...
验证码启动中...
备用人机验证