Electrostatic field

静电场，指的是观察者与电荷量不随时间发生变化的电荷相对静止时所观察到的电场。它是电荷周围空间存在的一种特殊形态的物质，其基本特征是对置于其中的静止电荷有力的作用。库仑定律描述了这个力。

电荷

• 带电现象： 物体经摩擦后对轻微物体有吸引作用的现象。

• 两种电荷：

  1. 将硬橡胶棒与毛皮摩擦后所带的电荷称为负电荷。
  2. 把玻璃棒与丝绸摩擦后所带的电荷称为正电荷。

• 电荷的基本性质： 电荷与电荷之间存在相互作用力，同种电荷相斥，异种电荷相吸。

• 微观解释： 物体因得失电子而带电荷。得到电子带负电；失去电子带正电。电荷是物质的一种基本属性，就象质量是物质一种基本属性一样。物体带电的本质是其电荷的迁移和重新分配。

• 电荷的量子化： $q=ne$ ， $(n=1,2,3,……)$ 。任何带电体所带电量都是基本电量的整数倍，这种电量只能取分立的、不连续的量值的性质称为电荷的量子化。

• 第一次测量到元电荷：密立根油滴实验 (1909)

• 元电荷： $e= 1.602 × 10^{-19} C$

• 电荷守恒定律： 在一个孤立系统中，无论发生了怎样的物理过程，电荷不会创生，也不会消失，只能从一个物体转移到另一个物体上，或从物体的一部分移到另一部分，即在任何过程中，电荷的代数和是守恒的。

• 点电荷： 当带电体的大小和带电体之间的距离相比很小时，可以忽略其形状和大小，把它看作一个带电的几何点。

库伦定理

• 库伦定理：
  $$\begin{aligned}F=k\frac{q_{1}q_{2}}{r^{2}}(k=8.987551787 \times 10^{9} (N\cdot m^{2} \cdot C^{-2}))\end{aligned}$$

• 使用条件：真空中的点电荷，只适用于静电场，也就是电荷都平衡静止。描述的是电荷间的力的大小。当电荷运动时，这个力发生变化，我们可以用新的定律来描述力的规律，也可以保留静电力的概念靠引入另一个力来修正。

• 真空中的介电常数（真空中的电容率）：
  $$\begin{aligned}\varepsilon_{0}=\frac{1}{4\pi k}=8.854187818 \times 10^{-12}（C^{2} \cdot N^{-1} \cdot m^{-2}）\end{aligned}$$

电场

• 电场： 电荷周围存在着的一种特殊物质。可以用虚拟的电场线来表示，这一概念在19世纪初由法拉第提出。

• 静电场： 相对于观察者静止的电荷在周围空间激发的电场

• 电场力： 电场对电荷的作用力

• 电场强度：
  $$\begin{aligned}E=\frac{F}{q}=k\frac{Q}{r^{2}}=\frac{1}{4\pi \varepsilon_{0}}\frac{Q}{r^{2}}\end{aligned}$$

• 注意电场强度是矢量，与F方向相同，单位：N/C

• 电场强度的大小只与产生电场的电荷（场源电荷）有关，而与试探电荷无关。

• 电场强度叠加原理：点电荷系在空间某点激发的电场强度，等于各点电荷单独存在时在该点激发电场强度的矢量和。

• 计算不是点电荷的带电物体的电场强度： 积分$E=\int_{}^{}\frac{dq}{4\pi \varepsilon_{0 } r^{2}}$ 。注意是矢量。对于矢量积分常用的方法就是把它分解到各个坐标轴上分别积分，再算出最后的矢量和。

电偶极子

• 电偶极子： 大小相等，符号相反且存在一微小间距的两个点电荷构成的复合体。

• 电偶极矩（电矩）： $p=ql$ 。矢量，方向由负电荷指向正电荷。

• 电偶极子延长线上任意一点P场强：
  $$\begin{aligned}E_{p}\approx \frac{p}{2\pi \varepsilon_{0} r^{3}}=k\frac{2p}{r^{3}}\end{aligned}$$ （如图摆放两个点电荷，以电偶极矩 $p$ 的方向为正方向， $r$ 可正可负。当算出来场强为正，则与电偶极矩方向相同；场强为负，则与电偶极矩方向相反）
  先计算出两点的场强:
  $$\begin{aligned}E_{+}=\frac{q}{4\pi \varepsilon_{0} (r-\frac{l}{2})^{2}} 、 E_{-}=\frac{-q}{4\pi \varepsilon_{0} (r+\frac{l}{2})^{2}}\end{aligned}$$
  最后计算矢量和:
  $$\begin{aligned}E_{p}=E_{+}+E_{-}=\frac{q}{4\pi \varepsilon_{0}}[\frac{1}{ (r-\frac{l}{2})^{2}}-\frac{1}{ (r+\frac{l}{2})^{2}}] =\frac{q}{4\pi \varepsilon_{0}} \frac{2rl}{r^{4}} \frac{1}{(1-\frac{l^{2}}{4r^{2}})^{2}}\end{aligned}$$
  因为电偶极子的定义就是微小间距，所以可以视作 $r\gg l$ ，所以 $\frac{l^{2}}{4r^{2}} \approx 0$ $\Rightarrow \frac{1}{(1-\frac{l^{2}}{4r^{2}})^{2}}\approx 1$ 。所以 $E_{p} \approx \frac{2ql}{4\pi \varepsilon_{0} r^{3}}=\frac{2p}{4\pi \varepsilon_{0} r^{3}}$

• 电偶极子垂线上任意一点P场强： $$\begin{aligned}E_{p} \approx\frac{p}{4\pi \varepsilon_{0} r^{3}}=k\frac{p}{ r^{3}}\end{aligned}$$ （方向与电偶极矩 $p$ 方向相反）

一些特殊情况的电场强度

真空中均匀带电直线 $L$ ，电荷线密度是 $\lambda$ ,则P点的场强

• 一般情况

  1. $E_{x}= \frac{\lambda }{4\pi \varepsilon_{0} a} (sin\theta_{2}-sin\theta_{1})$
  2. $E_{y}= \frac{\lambda }{4\pi \varepsilon_{0} a} (cos\theta_{1}-cos\theta_{2})$

• 无限长直导线

  1. $E_{x}=0$
  2. $E_{y}=\frac{\lambda}{2\pi \varepsilon_{0} a}$
     

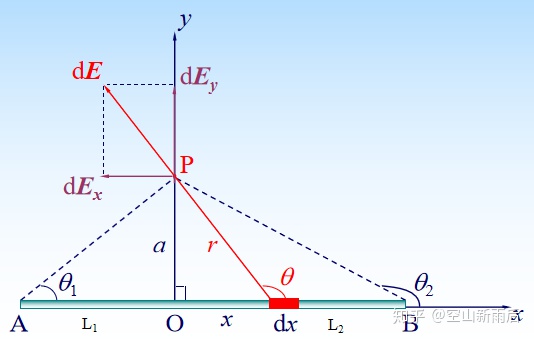
• 电荷q均匀地分布在一半径为R 的圆环上。则在在圆环的轴线上离圆环中心O距离为x的P点的场强*

• $$\begin{aligned}E=\frac{qx}{4\pi \varepsilon_{0} (x^{2}+R^{2})^{\frac{3}{2}}}\end{aligned}$$
  场强方向沿x轴正方向

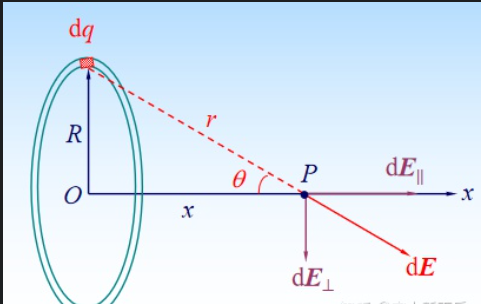
电荷q均匀地分布在一半径为R 的圆盘上,则在圆盘的轴线上离圆环中心O距离为x的P点的场强

• $$\begin{aligned}E=\frac{q}{2\pi\varepsilon_{0} R^{2}}(1-\frac{x}{\sqrt{x^{2}+R^{2}}})\end{aligned}$$

高斯定理

• 电场线： 描述电场分布情况的曲线。比较直观、形象。

• 曲线上每一点的切线方向表示该点处电场强度的方向。

• 垂直通过单位面积的电场线条数，在数值上就等于该点处电场强度的大小。即：电场线的疏密反映该点处电场强度的大小。 $E=\frac{dN}{dS_{\bot}}$ （ $N$ 通过单位面积的电场线条数， $S_{\bot}$ 单位面积）

• 电场线起始于正电荷（或无限远），终止于负电荷（或无限远）。

• 电场线不闭合，不相交。

• 电通量： $\Phi_{e}=ES$ （ $E$ 电场强度， $S$ 垂直于电场方向的面积，若不垂直需要把它投影到垂直方向上。） 若是电场不均匀，就积分
  对于闭合曲面规定：外法线方向为正

  1. 当 $\theta< 90°$ 时 $\Phi_{e} > 0$ ：电场线穿出闭合曲面。
  2. 当 $\theta> 90°$ 时 $\Phi_{e} < 0$ ：电场线穿进闭合曲面。
  3. 当 $\theta= 90°$ 时 $\Phi_{e} = 0$ ：电场线与曲面相切。

• 高斯定理： $\phi_{e}=\oint_{S}^{}EdS=\frac{1}{\varepsilon_{0}}\sum_{i=1}^{n}{q_{i}}$ 。在真空中，通过任一闭合曲面（高斯面）的电场强度通量等于该曲面所包围的所有电荷的代数和（所有电荷带电量带着符号相加）的 $\frac{1}{\varepsilon_{0}}$ 倍。

静电场环路定理

• 静电环路定理：在点电荷的电场中，电场力对试验电荷q0所做的功与路径无关，只和试验电荷q0的始、末两个位置有关。
• 静电场中电场强度的环流恒等于零。（电场力做功与路径无关。） $\oint_{l}^{}E dl=0$ 。简单来说就是沿着经典场内任意一条闭合曲线，他们的电场强度的积分一定是0。
• 描述静电场性质的两条基本定理：
  1. 高斯定理：静电场是有源场。**高斯定理将静电场与场源电荷联系了起来，揭示了静电场是有源场这一普遍性质。 简单来说就是有静电场，那么一定就有带电物体，它不是凭空产生的。
  2. 静电场环路定理：静电场是有势场（无旋场），保守力场。有势场（无旋场）：其电场线永不闭合。

电势

• 电势能： $E_{a}=q_{0}\int_{a}^{\infty}E \cdot dl$ （ $E、l$ 都是向量，向量点乘，就是高中的只取有效的位移），带电量为 $q_{0}$ 的电荷，在位置a的电势能在数值上就等于将其从a处移至势能的零点电场力所做的功。

• 电势能的零点可以任意选取，但是在习惯上，当场源电荷为有限带电体时，通常把电势能的零点选取在无穷远处。

• 电势能仅与电荷q0及其在静电场中的位置有关。可见电势能是属于电场和位于电场中的电荷q0所组成的系统的，而不是属于某个电荷的。其实质是电荷与电场之间的相互作用能。

• 电势能可正可负，是标量。具体取决于零势面在哪里。

• 电势：
  $$\begin{aligned}U_{a}=\frac{E_{a}}{q_{0}}=\int_{a}^{\infty}E \cdot dl\end{aligned}$$
  （ $E、l$ 都是向量，向量点乘），电场中a点的电势，在数值上等于把单位正电荷从a点移到电势能的零点处电场力所做的功。

• 点电荷产生的静电场： $U_{a}=\int_{a}^{\infty}E \cdot dl=\frac{Q}{4 \pi \varepsilon_{0} }(\frac{1}{r_{a}}-\frac{1}{r_{0}})$ 。以距离点电荷 $r_{0}$ 为0势能面。 $r_{a}$ 是其距离点电荷的距离。 $Q$ 是点电荷的带电量。

• 电势差：
  $$\begin{aligned}U_{ab}=U_{a}-U_{b}==\int_{a}^{\infty}E \cdot dl-\int_{b}^{\infty}E \cdot dl=\int_{a}^{b}E \cdot dl\end{aligned}$$
  静电场中a,b两点的电势差，等于将单位正电荷从a点移到b点电场力所做的功。电势差与零势能面的选取无关。电场力所做的功就是 $W_{ab}=q_{0}U_{ab}$

• 电势叠加原理： $U_{a}=\sum_{i=1}^{n}{U_{i}}$ ，点电荷系电场中任一点的电势，等于各个点电荷单独存在时在该点处的电势之代数和。对于连续带电体，就用积分。

• 等势面： 静电场中，电势相等的点所组成的曲面。

  1. 相邻等势面之间的电势差相等。
  2. 等势面与电场线处处正交。
  3. 电场线指向电势降低的方向。
  4. 等势面和电场线密集处电场强量值大，稀疏处电场强量值小。

导体的静电平衡

• 金属导体特征： 存在大量的自由电子。
• 静电感应： 在外电场影响下，导体表面不同部分出现正负电荷的现象。
• 静电平衡： 导体内部和表面没有电荷的宏观定向运动。
• 感应电荷： 因静电感应而在导体两侧表面上出现的电荷。
• 静电平衡时导体中的电场特性：
  1. 导体内部的电场强度处处为零。且导体表面的电场强度垂直于导体的表面。
  2. 导体内部和导体表面处处电势相等，整个导体是个等势体。
• 产生过程： 导体内部的自由电子在电场力的作用下产生定向移动，使导体一端带正电一段带负电。这个过程会不断发生，直到内部产生的感生电场与外部的电场抵消，内部的电场强度为0，电子才会停止移动，达到平衡状态。

电荷分布

• 在静电平衡下，导体所带的电荷只能分布在导体的表面，导体内部没有净电荷。 简单来说，空心导体和实心导体是等价的。在导体内部任取一个闭合的高斯面， $\oint_{S}^{}EdS=\frac{1}{\varepsilon_{0}}\sum_{}^{}{q_{i}}$ 。因为电场强度为0，那么等式左边就是0， $\varepsilon_{0}\ne 0$ ，所以电荷和为0。
• 处于静电平衡的导体，其表面上各点的电荷密度与表面邻近处场强的大小成正比。 取一个非常贴近表面的很小的圆柱形高斯面。因为高斯定理，还有静电平衡，那么感生电场和外部电场应该大小相等， $EdS=\frac{\sigma dS}{\varepsilon_{0}}$（ $\sigma$ 是电荷的面密度） ，所以 $E=\frac{\sigma}{\varepsilon_{0}}$ 。
• 静电平衡下的孤立导体，其表面处电荷密度 $\sigma$ 与该表面曲率有关，曲率（1/R）越大的地方电荷密度也越大，曲率越小的地方电荷密度也越小。

空腔导体

• 腔内的电场强度为零，不管外界的电场怎样。
• 电荷只分布在外表面上，内表面处处无电荷。
• 腔内有电荷的情况：空腔内表面所带电荷与腔内带电体所带电荷的代数和为零。 选取一个壳体内高斯面。因为导体内场强为0。所以内表面和电荷的代数和是0。在外部还可以选择高斯面，整个外部的电场就等效于一个带电荷的壳体产生的电场。

静电屏蔽

在接地的导体壳作用下，壳内的电荷所激发的电场，无法作用到壳外，内外电场互不干扰。

电介质

• 电介质：电阻率很大，导电能力很差的物质，即绝缘体。

• 常温下电阻率大于 $10^7 \Omega \cdot m$ （金属导体电阻率约为 $10^{-8} \Omega \cdot m$ ~ $10^{-6} \Omega \cdot m$ ）

• 电介质的特点：

  1. 分子中的正负电荷束缚得很紧，介质内部几乎没有自由电荷。
  2. 外电场作用下，电子一般也只能相对于原子核有一微观的位移。
  3. 实验发现，即使电介质在外电场中，其表面也会出现电荷。

电介质的极化

• 有极分子：分子的正、负电荷中心在无外场时不重合，分子存在固有电偶极矩。（常见的水、氨气等）有极分子在外场中发生偏转而产生的极化称为取向极化（转向极化）。

• 在没有外场的时候，分子杂乱无章的排列，整体显电中性。当有外来电场的时候，分子开始朝着同一个方向排列。首尾相接，就在最表面形成了带电现象。一端正电，一端负电。

• 无极分子：分子的正、负电荷中心在无外场时重合，不存在固有分子电偶极矩。（常见的甲烷等）无极分子在外场的作用下由于正负电荷发生偏移而产生的极化称为位移极化。

• 在没有外场的时候，正电中心，负电中心都是重合的，整体显电中性。有外场的时候，正电中心和负电中心在电场力的作用下，发生细微的偏移，最后呈现正电中心和负电中心不重合，导致了表面的带电现象。

• 束缚电荷（极化电荷）： 因为并不是像导体那样电子自由移动，从一段跑到了另外一段而带电。电介质中的电子是几乎没有移动的，这种由于极化，在介质表面产生的电荷称为极化电荷或称束缚电荷。

• 击穿： 在强电场作用下电介质变成导体的现象。

• 压电性： 在机械力作用下能产生极化

• 铁电性： 被外电场极化后，去掉外电场电介质仍能保持极化状态。

极化强度

• 电极化强度： $P=\frac{\sum_{}^{}{p_{i}}}{\Delta V}=\chi_{e}\varepsilon_{0}E$ 。（ $p_{i}$ 每个分子的电偶极矩（矢量）， $\Delta V$ 电介质体积。 $\chi_{e}$ 介质的电极化率只取决于电介质的种类， $\varepsilon_{0}$ 真空中的介电常数， $E$ 电场强度（矢量））

• 矢量 ，方向是所有电偶极矩的矢量和

• 单位， $C\cdot m^{-2}$

• $\sum_{}^{}{p_{i}}=0$ 没极化， $\sum_{}^{}{p_{i}}\ne 0$ 有极化。

• 电极化强度与极化电荷的关系： $\sigma ‘=\left| P\right|cos\theta=P_{n}$ （ $\theta$ 是极化强度的方向与该处平面法线的夹角。 $\sigma ‘$ 是该处的电荷面密度）均匀电介质表面上产生的极化电荷面密度，在数值上等于该处电极化强度在表面法向上的分量。

• 带电的性质

  1. $\theta < \frac{\pi}{2}$ ，该处表面出现正极化电荷
  2. $\frac{\pi}{2} < \theta < \pi$ ，该处表面出现负极化电荷
  3. $\theta =\frac{\pi}{2}$ ，该处表面无极化电荷

• $\oint_{}^{}PdS=-\sum_{}^{}{q_{i}}$ 。电极化强度通过封闭曲面S的通量等于因极化而移出S面的极化电荷总量。根据电荷守恒定律，也等于留在S面所包围体积内极化电荷总量的负值。

有介质的高斯定理

• 公式：$\oint_{S}^{}DdS=\sum_{}^{}{q_{i}}$ ，在静电场中，通过任意封闭曲面的电位移通量等于该曲面所包围的自由电荷的代数和。

• $D=\varepsilon_{0}E+P$ $=(1+\chi_{e})\varepsilon_{0}E$ ，电位移矢量（这里的电场强度与极化强度都是矢量，求的是矢量相加）

• 相对介电常数： $\varepsilon_{r}=1+\chi_{e}$ ，所以原公式就是 $D=\varepsilon_{r}\varepsilon_{0}E$

• $q_{i}$ 是自由电荷

电容

• 电容： 导体具有储存电荷的本领 （储存电能）

• 公式： $C=\frac{q}{U}$ ，孤立导体所带电荷量q与其电势U 的比值。电容C是使导体升高单位电势所需要的电量。

• 单位：F（法拉）

• $1F=10^{6}\mu F=10^{12}pF$

• 孤立导体的电容仅取决于导体的几何形状和大小，与导体是否带电无关。

• 地球的电容大小： $7.11 \times 10^{-4} F$

• 孤立导体球的电容： $C=4\pi \varepsilon_{0}R$

电容器

• 电容器：由电介质隔开的两块任意形状导体（极板）组合而成。

• 电容器电容： $C=\frac{q}{U_{AB}}$ ，极板电荷量q（绝对值）与极板间电势差 $U_{AB}$ 之比值。

• 三种常见电容器的电容：

• 平行板电容器： $C=\frac{\varepsilon_{0}\varepsilon_{r}S}{d}$ （ $S$ 平行板的面积， $d$ 平行板间距， $\varepsilon_{0}$ 真空中的电容率， $\varepsilon_{r}$ 相对电容率）

• 同心球电容器： $C=\frac{4\pi \varepsilon_{0} \varepsilon_{r} R_{B}R_{A}}{R_{B}-R_{A}}$ （$\varepsilon_{0}$ 真空中的电容率， $\varepsilon_{r}$ 相对电容率， $R_{B}$ 外球壳半径， $R_{A}$ 内球壳半径）

• 圆柱形电容器： $C=\frac{2\pi \varepsilon_{0} \varepsilon_{r} l}{ ln\frac{R_{B}}{R_{A}}}$ （ $\varepsilon_{0}$真空中的电容率， $\varepsilon_{r}$ 相对电容率， $R_{B}$ 外圆柱壳半径， $R_{A}$ 内圆柱壳半径， $l$ 圆柱体的高度）

电容器的联结

• 电容器的串联： $\frac{1}{C_{和}}=\frac{1}{C_{1}}+\frac{1}{C_{1}}+…+\frac{1}{C_{n}}$
• 电容器的并联： $C_{和}=C_{1}+C_{2}+…+C_{n}$ 。

静电场的能量

• 点电荷系的电能： $W=\frac{1}{4\pi \varepsilon_{0}}\frac{q_{1}q_{2}}{r}$ 。将q2从无限远处移动到b点，外力要克服q1的电场力做功W。根据能量守恒定律，外力所做的功等于该带电系统静电能的增量。

• 电容的能量：
  $$\begin{aligned}W_{e}=\frac{1}{2}QU_{AB}=\frac{1}{2}\frac{Q^{2}}{C}=\frac{1}{2}CU_{AB}^{2}\end{aligned}$$

• 电场的能量： $W_{e}=\frac{1}{2}\varepsilon_{0}\varepsilon_{r}E^{2}V$

• 电场的能量密度： $\omega_{e}=\frac{1}{2}\varepsilon_{0}\varepsilon_{r}E^{2}$