晶体三极管
请注意,本文最近一次更新于:2022-03-12,文章内容可能已经不具有时效性,请谨慎参考
本文最后更新于:2022年3月12日星期六晚上6点26分 +08:00
三极管,全称应为半导体三极管,也称双极型晶体管、晶体三极管,是一种控制电流的半导体器件。其作用是把微弱信号放大成幅度值较大的电信号,也用作无触点开关。三极管是半导体基本元器件之一,具有电流放大作用,是电子电路的核心元件。三极管是在一块半导体基片上制作两个相距很近的PN结,两个PN结把整块半导体分成三部分,中间部分是基区,两侧部分是发射区和集电区,排列方式有PNP和NPN两种。
1.3.1晶体管的结构及类型
采用NPN结构的晶体二极管,位于中间的P区称为基区,它很薄并且杂质浓度很低;位于上层的N区是发射区,掺杂浓度很高;位于下层的N区是集电区,面积很大.
从三个区域引出的三个电极分别为:基极b,发射极e和集电极c
发射区e和基区b之间的PN结称为发射结;基区b和集电区c之间的PN结称为集电结
1.3.2晶体管的电流放大作用
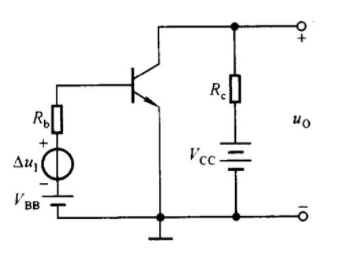
$\Delta u_1$为输入电压信号,接入基极-发射极回路,称为输入回路;放大后的信号在集电极-发射极回路,称为输出回路.由于发射极是两个回路的公共端,故称该电路为共射放大电路.
使晶体管工作在放大状态的外部条件是发射结正偏且集电极反偏,因此需要满足$V_{CC}>B_{BB}$
晶体二极管的发射作用表现为小的基极电流可以控制大的集电极电流
晶体管内部载流子的运动
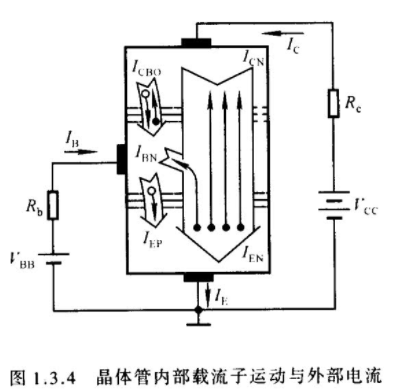
分析:
- 发射结加正向电压,多子扩散运动形成发射极电流$I_E$
因为发射结加载正向电压,并且发射区的掺杂程度很高,因此大量自由电子因扩散运动越过发射结到达基区;与此同时,基区的空穴也向发射区扩散,但是我们说NPN型的基区掺杂程度很低,因此空穴形成的电流非常小,近似分析时忽略不计. - 扩散到基区的自由电子与空穴复合形成基极电流$I_B$
由于我们说基区很薄并且掺杂程度很低,而且集电极加载反向电压,所以扩散到基区的电子中只有极少部分与空穴复合,其余部分均作为基区的非平衡少子到达集电结.又由于电源$V_{BB}$的作用,电子与空穴的复合运动将源源不断地进行,形成基极电流$I_B$ - 集电结加反向电压,少子漂移运动形成集电极电流$I_C$
由于集电结加反向电压并且集电结的面积大,基区的非平衡少子在外电场的作用下越过集电结到达集电区,形成漂移电流.与此同时,集电区与基区的平衡少子也参与漂移运动,但他的数量很少,近似分析时忽略不计.可见在集电极电源$V_{CC}$的作用下,漂移运动形成集电极电流$I_C$晶体管的电流分配关系
- 发射结加正向电压,多子扩散运动形成发射极电流$I_E$
提要:
- 由发射区向基区扩散所形成的电子电流为$I_{EN}$
- 基区向发射区扩散所形成的空穴电流为$I_{EP}$
- 基区内复合运动所形成的电流为$I_{BN}$
- 基区内非平衡少子飘逸到集电区所形成的电流为$I_{CN}$
- 平衡少子在集电区与基区之间的漂移运动所形成的电流为$I_{CBO}$
- 穿透电流$I_{CEO}$ = (1 + $\beta$)$I_{CBO}$,是在基极开路时集电极与发射极之间形成的电流

根据上图所示,可以得到一下电流关系
$$\begin{aligned}
I_E = I_{EN} + I_{EP} = I_{BN} + I_{CN} + I_{EP}
\end{aligned}\tag{1.3.1}$$
$$\begin{aligned}
I_C = I_{CN} + I_{CBO}
\end{aligned}\tag{1.3.2}$$
$$\begin{aligned}
I_B = I_{BN} + I_{EP} - I_{CBO} = I_B’ -I_{CBO}
\end{aligned}\tag{1.3.3}$$
从外部看:
$$\begin{aligned}
I_E = I_B + I_C
\end{aligned}\tag{1.3.4}$$晶体管的共射电流放大系数
电流$I_{CN}$与$I_B’$之比称为共射直流电流放大系数$\bar{\beta}$,根据式$(1.3.2)$和式$(1.3.3)$可以得到:
$$\begin{aligned}
\bar{\beta} = \frac{I_{CN}}{I_{B}’} = \frac{I_C - I_{CBO}}{I_{B} + I_{CBO}}
\end{aligned}\tag{1.3.5}$$
整理可以得到:
$$\begin{aligned}
I_C = \bar{\beta}I_B + (1 + \bar{\beta})I_{CBO} = \bar{\beta}I_B + I_{CEO}
\end{aligned}\tag{1.3.5}$$
式中$I_{CEO}$称为穿透电流,其物理意义是,当基极开路时($I_B$ = 0),在集电极电源$V_{CC}$的作用下集电极与发射极之间形成的电流,而$I_{CBO}$是发射极开路时,集电极的反向饱和电流.一般情况下,$I_B >> I_{CBO}, \bar{\beta} >> 1$,所以
$$\begin{aligned}
I_C ≈ \bar{\beta}I_B
\end{aligned}\tag{1.3.6}$$
$$\begin{aligned}
I_E ≈ (1 + \bar{\beta})I_B
\end{aligned}\tag{1.3.7}$$若有输入电压$\Delta u_1$作用,则晶体管的基极电流将在$I_B$的基础上叠加动态电流$\Delta i_B$,当然集电极电流也会在$I_C$的基础上叠加动态电流$\Delta i_c$,$\Delta i_c$与$\Delta i_b$之比称为共射交流电流的放大系数,记作$\beta$,即:
$$\begin{aligned}
\beta = \frac{\Delta i_C}{\Delta i_B}
\end{aligned}\tag{1.3.8}$$
在$\Delta i_B$不大的情况下,可以认为: $\beta = \bar{\beta}$当以发射极电流作为输入电流,以集电极电流作为输出电流时,$I_{CN}$与$I_E$之比称为共基直流电流放大系数,记为$\bar{\alpha}$,即:
$$\begin{aligned}
\bar{\alpha} = \frac{I_{CN}}{I_E}
\end{aligned}$$
根据前述关系可以得到$\bar{\alpha}$与$\bar{\beta}$之间的关系:
$$\begin{aligned}
\bar{\alpha} = \frac{\bar{\beta}}{1 + \bar{\beta}} 或 \bar{\beta} = \frac{\bar{\alpha}}{1 - \bar{\alpha}}
\end{aligned}\tag{1.3.11}$$
参照前述可以定义共基交流电流放大系数,并在通常情况下有:$\alpha$ ≈ 1,$\bar{\alpha}$ = $\alpha$1.3.3晶体管的共射特性曲线
输入特性曲线
输入特性曲线描述晶体管压降$U_{CE}$一定的情况下,基极电流$i_B$与发射结压降$u_{BE}$之间的函数关系,即:
$$\begin{aligned}
i_B = f(u_{BE})|_{U_{CE} = const}
\end{aligned}\tag{1.3.13}$$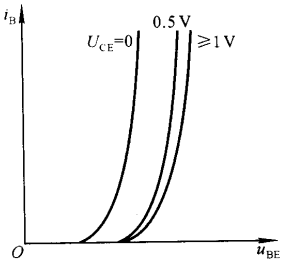
- 当$U_{CE}$ = 0时,相当于集电极与发射极短路,相当于集电结与发射结并联,此时的输入特性曲线与PN结相似
- 当$U_{CE}$增大时,曲线将向右移动,这是因为由发射区注入基区的非平衡少子有一部分越过基区和集电结形成集电极电流$i_C$,使得在基区参与复合运动的非平衡少子随这电压的增大而减少;因此想要获得同样的$i_B$就势必需要增大$u_{BE}$,使得发射区向基极注入更多的电子
- 但是当$U_{CE}$增大到一定程度后,发射区注入基区的绝大多数非平衡少子都已经被收集到了集电区,因而再增大$U_{CE}$,电流$i_C$也不可能再明显增大,也就是说,$i_B$已经基本不变,此后的曲线将基本重合.
- 集电极电流可以如下表示:
$$\begin{aligned}
I_C = I_Se^{\frac{V_{BE}}{U_T}} = \bar{\beta}I_B
\end{aligned}$$输出特性曲线
输出特性曲线描述基极电流$I_B$为一常量时,集电极电流$i_C$与晶体管压降$U_{CE}$之间的函数关系,即:
$$\begin{aligned}
i_C = f(u_{CE})|_{I_B = const}
\end{aligned}\tag{1.3.14}$$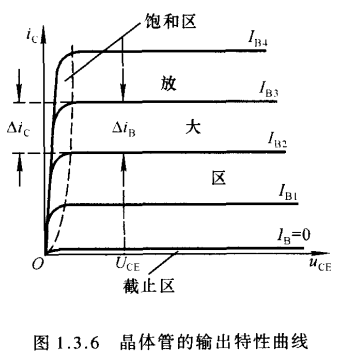
- 当$U_{CE}$增大到一定程度后,发射区注入基区的绝大多数非平衡少子都已经被收集到了集电区,因而再增大$U_{CE}$,电流$i_C$也不可能再明显增大,此后的曲线将基本平行于横轴.
- 从输出特性曲线的图像上看,晶体管有三个工作区域:
- 截止区
其特征是发射结电压小于开启电压并且集电结反向偏置 - 放大区
其特征是发射结正向偏置且集电结反向偏置,对于共射电路,此时$i_C$几乎仅仅取决于$i_B$,表现出$i_B$对$i_C$的控制作用,$i_C$ = $\beta i_B$ - 饱和区
其特征是发射结与集电结均处于正向偏置,对于共射电路,此时$i_C$不仅与$i_B$有关,而且随着$u_{CE}$增大而增大,$i_C$ < $\beta i_B$.实际电路中,若晶体管的$u_{BE}$增大时$i_B$随之增大但$i_C$几乎保持不变,则说明晶体管进入饱和区 - 倒置区(反向有源区)
除了上述三个工作状态区意外,当发射结反偏,集电结正偏时,就会形成倒置区,也叫做反向有源区.实际上是将发射结当作集电结,集电结当作发射结来使用. - 临界饱和区
当基极-发射极电压等于集电极-发射极电压时,集电结电压为零,晶体管处于临界饱和区,b-c直接相连的模型称为二极管联接型,在现实中十分常见
- 截止区
- 基区宽度调变效应
- 集电极-发射极电压等于基极-发射极的正向电压与基极-集电极的反向电压之和.当集电极-发射极电压发生变化时,由于基极-发射极的正向电压变化很小,因此基极-集电极电压的增量近似等于集电极-发射极的电压增量.而集电极-发射极电压改变会引起集电结反向电压增大、集电结势垒区加深,从而使得实际基区宽度变窄.而基区宽度变窄,会使得共射直流放大系数$\beta$增大.反映到输出曲线上,就是随着集电极-发射极电压增大,线间间距加宽,于是曲线出现倾斜
- 考虑此效应后,将各条曲线反向延长并交汇与坐标轴,会发现在水平轴上各延长线几乎交汇于一点,定义该点对应的电压为**厄利电压$V_A$**,且$V_A$为正值.
考虑厄利电压后,集电极电流的增量为:
$$\begin{aligned} \Delta I_C = \frac{\Delta I_C(0)}{V_A}\times V_{CE} \end{aligned}$$
$I_C(0)$是临界饱和状态时集电极电流.
由此,我们可以得到任意集电极-发射极电压下的集电极电流:
$$\begin{aligned}
I_C = I_C(0)(1 + \frac{V_{CE}}{V_{A}})
\end{aligned}$$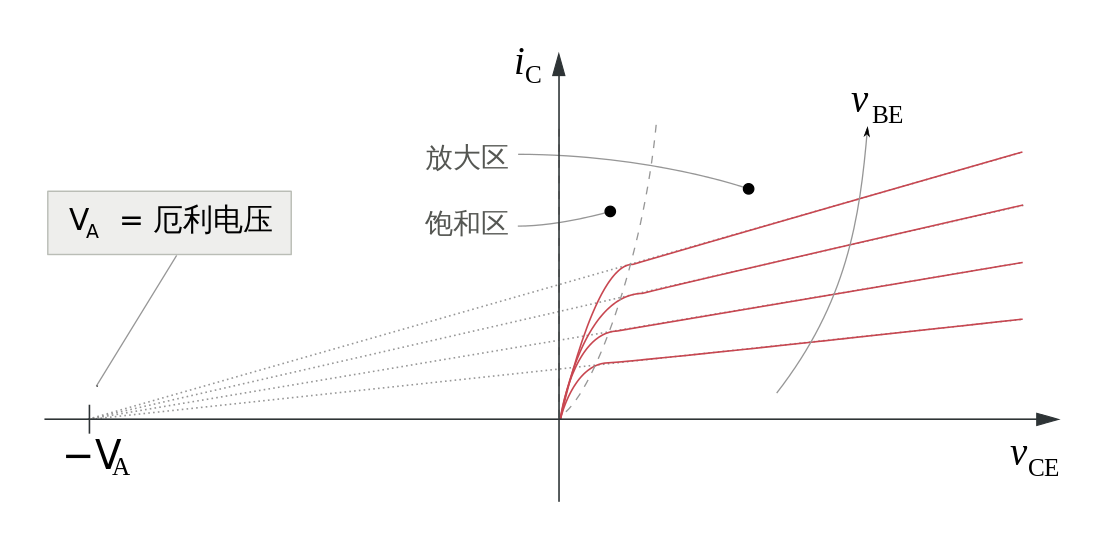
1.3.4晶体管的主要参数
直流参数
- 共射直流放大系数
- 共基直流放大系数
- 极间反向电流
$$\begin{aligned}\bar{\beta} = \frac{I_C - I_{CEO}}{I_B}\end{aligned}$$
当$I_C >> I_{CEO}$时,$\bar{\beta} ≈ \frac{I_C}{I_B}$$$\begin{aligned}\bar{\alpha} = \frac{I_{CN}}{I_E} = \frac{I_C - I_{CBO}}{I_E}\end{aligned}$$
$$\begin{aligned}
\bar{\alpha} = \frac{\bar{\beta}}{1 + \bar{\beta}} \\
\bar{\beta} = \frac{\bar{\alpha}}{1 - \bar{\alpha}}
\end{aligned}\tag{1.3.11}$$
当$I_{CBO}$可以忽略时,$\bar{\alpha} ≈ \frac{I_C}{I_E}$
- $I_{CBO}$是发射极开路时,集电结的反向饱和电流,$I-{CEO}$是基极开路时,集电极与发射极之间的穿透电流,$I_{CEO} = (1 + \bar{\beta})I_{CBO}$.反向电流越小,性能越稳定.
交流参数
1.共射交流放大系数
2.共基交流放大系数
3.特征频率 - $$\begin{aligned}\beta = \frac{\Delta i_C}{\Delta i_B}\end{aligned}$$
在$\Delta i_B$不大的情况下,可以认为: $\beta = \bar{\beta}$
$\beta$值太小的放大能力不强,太大的温度稳定性差. - 参照前述可以定义共基交流电流放大系数,并在通常情况下有:$\alpha$ ≈ 1,$\bar{\alpha}$ = $\alpha$
- 特征频率$f_T$:
由于晶体管中PN结结电容的存在,晶体管的交流电流放大系数是所加信号频率的函数.信号频率高到一定程度时,集电结电流与基极电流之比不但数值下降,而且会产生相移.使共射电流放大系数数值下降到1的信号频率称为特征频率极限参数
1.最大集电极耗散功率
2.最大集电极电流
3.极间反向击穿电压 - 最大集电极耗散功率$P_{CM}$:
$P_{CM}$取决于晶体管的温升.对于确定型号的晶体管,$P_{CM}$是一个确定值:
$$\begin{aligned}P_{CM} = i_Cu_{CE} =常数\end{aligned}$$
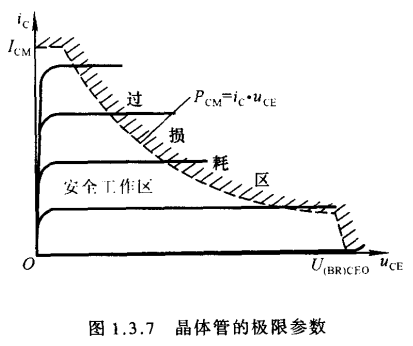
在输出特性坐标平面中为双曲线的一条,曲线的右上方为过损耗区 - 最大集电极电流$I_{CM}$:
$i_C$在相当大的范围内$\beta$值基本保持不变,但当$i_C$的数值达到一定程度时$\beta$的数值将下降.使得$\beta$值明显减小的$i_C$即为$I_{CM}$.
实际上当电流大于最大集电极电流时,晶体管不一定损坏,但共射交流放大系数会降低 - 晶体管某一电极开路时,另外两个电极间所允许加载的最高反向电压称为极间反向击穿电压,超过这一数值,晶体管会被击穿.
$U_{(BR)CBO}$是发射极开路时集电极-基极之间的反向击穿电压
$U_{(BR)CEO}$是基极开路时集电极-发射极之间的反向击穿电压
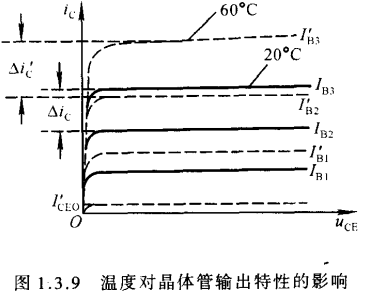
$U_{(BR)EBO}$是集电极开路时发射极-基极之间的反向击穿电压1.3.5温度对晶体管参数及其特性的影响
温度对$I_{CBO}$的影响
- 因为$I_{CBO}$是集电结加载反向电压时平衡少子的漂移运动形成的,所以当温度升高时,热运动加剧,更多的价电子将挣脱束缚,使得少子浓度增大,从外部看就是$I_{CBO}$增大.温度每升高10℃,$I_{CBO}增加约1倍$
温度对输入特性的影响
- 与二极管的伏安特性曲线相似,当温度升高时,正向特性曲线将左移
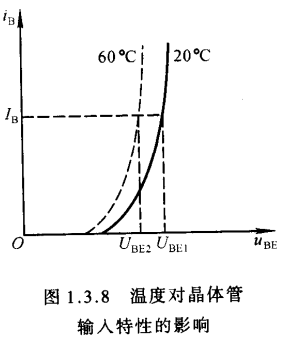
温度对输出特性的影响
- 温度升高时共射交流放大系数$\beta$增大,且输入特性曲线左移,集电极电流增大.
晶体管低频小信号等效模型
- 尽管晶体管的输入输出特性曲线都是非线性的,但是当输入信号很小时,局部范围内可以视为线性元件处理.晶体管在很小的范围内工作的模型就是小信号模型,小信号模型是一种线性模型.低频模型中容抗很大,因此结电容忽略不计
h参数等效模型
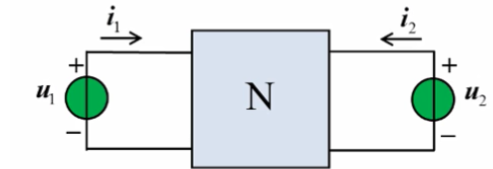
- h参数方程
$$\begin{cases} v_1 = h_{11}i_1 + h_{12}v_2
\ i_2 = h_{21}i_1 + h_{22}v_2 \end{cases}$$ - 共射h参数等效电路
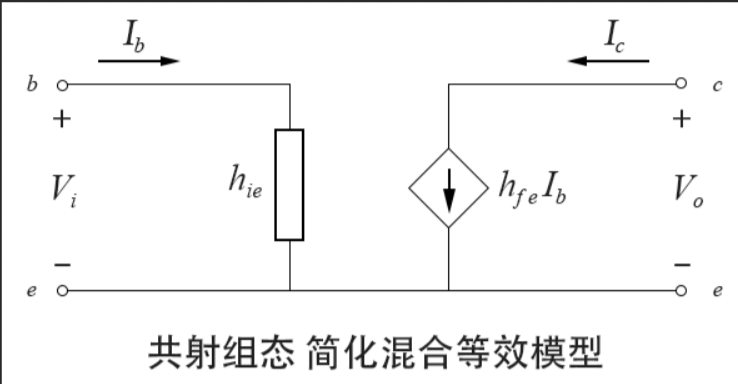
- 以共射为例:
$$\begin{cases} v_{be} = h_{ie}i_b + h_{re}v_{ce}
\ i_c = h_{21}i_b + h_{oe}v_{ce} \end{cases}$$
注意到:
$$\begin{aligned}
\beta = \frac{i_c - i_{ceo}}{i_b}
\end{aligned}$$
于是:$h_{21} = \beta$, $h_{oe} = \frac{i_{ceo}}{v_{ce}}$
方程的物理解释是基极-发射极电压等于一个压控电压源与电阻电压之和,输出电流等于流控电流源与并联电阻电流之和.
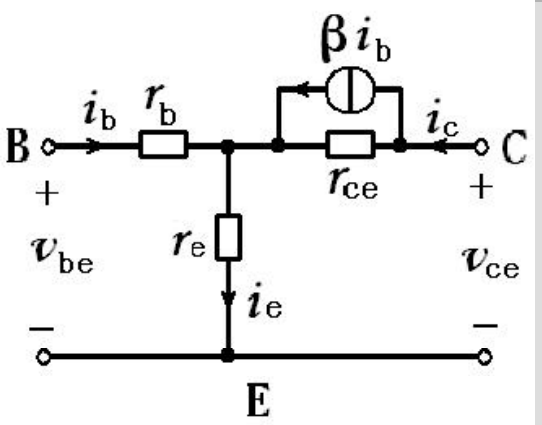
上图中是忽略了压控电压源与电阻电流后的简化电路. - 上图是共射组态的T型等效电路,电流从基极进入,从发射极输出
- 在小信号模型中,正偏置的发射极可以用交流电阻$r_e$来代替
$$\begin{aligned}
r_e=\frac{\Delta V_{BE}}{\Delta I_E}=\frac{\mathrm{d}V_{BE}}{\mathrm{d}I_E}
\end{aligned}$$
$$\begin{aligned}
I_E=I_B+I_C=I_C(1+\frac{1}{\beta})
\end{aligned}$$
$$\begin{aligned}
I_E=(1+\frac{1}{\beta})I_Se^{\frac{V_{BE}}{V_T}}
\end{aligned}$$
$$\begin{aligned}
\frac{\mathrm{d}I_E}{\mathrm{d}V_{BE}}=(1+\frac{1}{\beta})\frac{I_S}{V_T}e^{\frac{V_{BE}}{V_T}}
\end{aligned}$$
$$\begin{aligned}
r_e=\frac{V_T}{I_S(1+\frac{1}{\beta}e^{\frac{V_{BE}}{V_T}})}=\frac{V_T}{I_E}
\end{aligned}$$
小提一句,$r_e$的表达式十分重要,日后我们会经常不假思索地用到 - 此外,因为基区很薄,故对于基极电流来说,材料的体电阻不能忽略,在模型中用$r_b$表示,其数值一般为数十到数百欧姆
- 集电极电流受到基极电流控制,考虑到基区调变效应,因此在受控电流源上并联一个电阻$r_{ce}$,其数值等于集电极-发射极电压$V_{CE}$的变化量于集电极电流$I_C$的变化量之比
$$\begin{aligned}
I_C=I_Se^{\frac{V_{BE}}{V_T}}(1+\frac{V_{CE}}{V_A})
\end{aligned}$$
$$\begin{aligned}
r_{ce}=\frac{\Delta V_{CE}}{\Delta I_C}=\frac{V_A}{I_Se^{\frac{V_{BE}}{V_T}}}=\frac{V_A}{I_C}
\end{aligned}$$
其中$V_A$是厄利电压Π型等效电路
- 日后补充
命名规则


This is an identification card as an honored membership of FeynmanDirac
Happy to see you follow FeynmanDirac, enjoy science together
 验证码启动中...
验证码启动中...
备用人机验证