场效应管

场效应晶体管（Field Effect Transistor缩写(FET)）简称场效应管。主要有两种类型：结型场效应管（junction FET—JFET)和金属 - 氧化物半导体场效应管（metal-oxide semiconductor FET，简称MOS-FET）。由多数载流子参与导电，也称为单极型晶体管。它属于电压控制型半导体器件。具有输入电阻高（107～1015Ω）、噪声小、功耗低、动态范围大、易于集成、没有二次击穿现象、安全工作区域宽等优点，现已成为双极型晶体管和功率晶体管的强大竞争者。

• 声明： 本文中的相关参数符号在不同的书中所给予的符号可能有所不同，为避免读者疑惑，例如本文中将会提及的夹断电压$u_{GS(off)}$、开启电压$u_{GS(th)}$在某些书中会统一使用$v_T$替代、V替代u等，在实际意义上表述是一致的，特此声明

场效应管简介

• 场效应管(EFT)是利用输入回路的电场效应来控制输出回路电流的一种半导体器件
• 场效应管是仅靠半导体中的多数载流子导电，又称单极型晶体管

1.4.1结型场效应管

结型场效应管简介

• 结型场效应管共有N沟道和P沟道两种类型
  
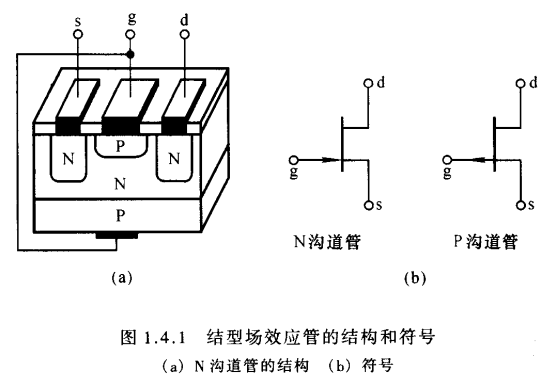
• 同一块N型半导体上制作两个高掺杂的P区，并将他们连接在一起，索引处的电极称为栅极g，N型半导体的两端分别引出两个电极，一个称为漏极d，一个称为源极s.
• P区与N区交界面形成耗尽层，漏极d与源极s间的非耗尽层区域称为导电沟道

结型场效应管的工作原理

• 为使N型沟道结型场效应管能正常工作，应该在其栅极-源极之间加载负向电压(即$U_{GS}<0$),以保证耗尽层承受反向电压;在漏极-源极之间加载正向电压$U_{DS}$,以形成漏极电流$i_D$.
• $U_{GS}$ < 0保证了栅极-源极之间内阻很高的特点，又实现了$U_{GS}$对沟道电流的控制.下面通过对栅极-源极电压$u_{GS}$和漏极-源极电压$u_{DS}$对导电沟道的影响，来说明管子的工作原理
  下图和分析均以N型沟道为例
  1. 当漏极-源极电压$u_{DS}$ = 0 V时(即漏极-源极短路)，$u_{GS}$对导电沟道的控制作用
     
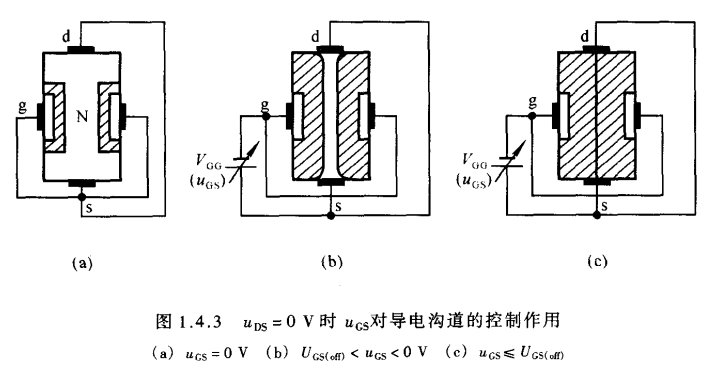
     • 当$u_{GS}$和$u_{DS}$都为0 V时，耗尽层很窄，导电沟道很宽，如(a)所示
     • 当$\lvert u_{GS} \rvert$增大时，耗尽层加宽，沟道变窄，如(b)所示
     • 当$\lvert u_{GS} \rvert$继续增大到某一数值时，耗尽层闭合，沟道消失，沟通电阻趋于无穷大，我们称此时的电压$u_{GS}$为夹断电压 $u_{GS(off)}$如(c)所示
  2. 当$u_{GS}$为$U_{GS(off)}$~0V中的某一固定数值时，$u_{DS}$对漏极电流$i_D$的影响
     
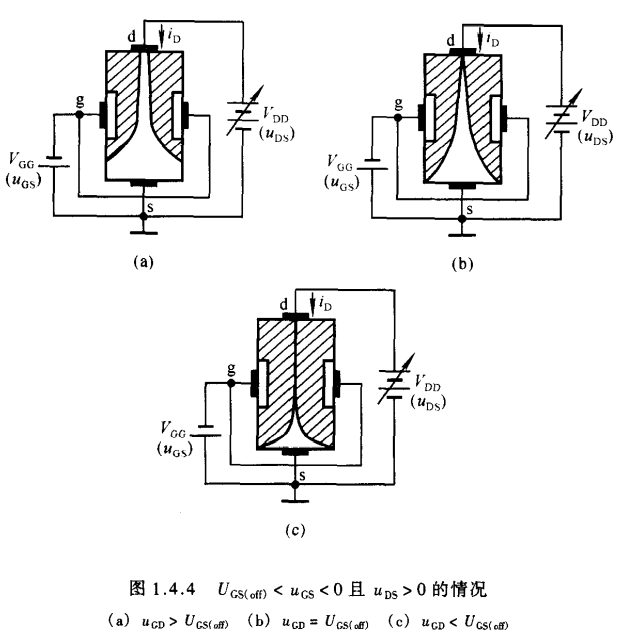
     • 当栅极-源极电压在夹断电压~0V之间的某一确定数值时，如果$u_{DS}$ = 0V，虽然存在由$u_{GS}$所确定的一定宽度的导电沟道，但由于d-s之间电压为零，多子不会产生定向移动，因而漏极电流$i_D$为零
     • 当$u_{DS}$ > 0V时，则有漏极电流从漏极流向源极，从而使得沟道中各点与栅极之间的电压不再相等，而是沿沟道从源极到漏极逐渐增大，造成靠近漏极的一端耗尽层比靠近源极的宽.换言之，靠近漏极的导电沟道比靠近源极的一边窄.如图(a)所示
     • 因为栅极-漏极电压$u_{GD}$ = $u_{GS}$ - $u_{DS}$，当$u_{DS}$逐渐从零增大时，$u_{GD}$将会逐渐减小，因而靠近漏极的一端的导电沟道必将随之变窄.但是，只要栅极-漏极间不出现夹断区域，沟道电阻仍将基本取决于栅极-源极电压$u_{GS}$
       因此，漏极电流$i_D$将随着$u_{DS}$增大而线性增大，d-s呈现电阻特性.
       但是一旦漏极-源极电压$u_{DS}$增大到使得$u_{GD}$等于夹断电压$u_{GS(off)}$，靠近漏极一侧的耗尽层就会出现夹断区，如图(b)所示，我们称$u_{GD}$ = $u_{GS(off)}$为预夹断
     • 此时若漏极-源极电压$u_{DS}$继续增大，$u_{GD}$<$u_{GS(off)}$耗尽层闭合部分将沿沟道延伸，使夹断区加长，如图(c).这时，一方面自由电子从漏极向源极定向移动所受到的阻力增大，导致漏极电流减小；另一方面随着$u_{DS}$增大，使d-s间的纵向电场增强，使漏极电流增强.实际上，两种作用将相互抵消，$u_{DS}$的增大几乎全部降落在夹断区，用于克服夹断区对漏极电流形成的阻力.因此，从外部看，在$u_{GD}$ < $u_{GS(off)}$的情况下，当$u_{DS}$增大时，漏极电流$i_D$几乎不变，这时$i_D$仅仅决定于$u_{GS}$，表现出恒流特性
  3. 当$u_{GD}$<$u_{GS(off)}$时，$u_{GS}$对漏极电流$i_D$的控制作用
     • 在$u_{GD}$ = $u_{GS}$ - $u_{DS}$ < $u_{GS(off)}$，即$u_{DS}$ > $u_{GS}$ - $U_{GS(off)}$，当$u_{DS}$为一常量时，对于确定的$u_{GS}$，就有确定的漏极电流.此时可以通过改变 $u_{GS}$ 来控制漏极电流的大小.由于漏极电流受栅极-源极电压的控制，故称场效应管为电压控制元件.
     • 对于晶体管，我们曾用共射交流放大系数$\beta$来描述动态情况下基极电流对集电极电流的控制作用($\beta$ = $\frac{\Delta i_C}{\Delta i_B}$)，类似的，对于场效应管我们用$g_m$来描述动态的栅极-源极电压对漏极电流的控制作用，$g_m$称为低频跨导
       $$\begin{aligned}
       g_m = \frac{\Delta i_D}{\Delta U_{GS}}
       \end{aligned}$$
• 整合总结一波
  1. 栅极g主要用于加载电压，栅极g的电流一般不考虑
  2. $V_{GS}(U_{GS})$控制沟道宽窄，反映沟道电阻；$V_{DS}(U_{DS})$控制沟道形状
  3. 没有漏极-源极电压$u_{DS}$存在或者$u_{DS}$过高都将不会存在电流
  4. 由以上分析可知：
     1. 在$u_{GD}$>$U_{GS(off)}$，对于不同的$u_{GS}$，d-s间等效为不同的阻值
     2. 在$u_{GD}$=$U_{GS(off)}$，d-s之间处于预夹断
     3. $u_{GD}$<$U_{GS(off)}$，$i_D$几乎仅仅取决于$u_{GS}$而与$u_{DS}$无关，此时可以近似看作为电压控制的电流源
  5. 由于本次推导全部采用的是N型结型场效应管模型，因此应当再次指出的是，对于N型场效应管中 $u_{GS}$ ≤ 0的;而对于P型结型场效应管 $u_{GS}$ ≥ 0，且对于P型结型场效应管，上述的结论中所有关系比较运算符将全部取反

结型场效应管的特性曲线

• 1. 输出特性曲线
     输出特性曲线描述当栅极-源极电压$u_{GS}$为常量时，漏极电流$i_D$与漏极-源极电压$u_{DS}$之间的函数关系
     $$\begin{aligned}
     i_D = f(u_{DS})\rvert_{u_{GS} = const}
     \end{aligned}$$
     对于一个确定的$u_{GS}$，就会有一条对应的曲线，因此输出特性为一曲线族，如图下所示.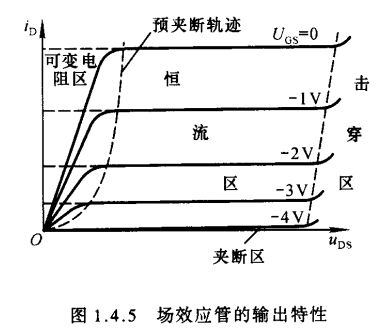
     
     场效应管存在三个工作区域：
     1. 可变电阻区
        可变电阻区也称非饱和区，图中的曲线为预夹断轨迹，根据前面所述 $u_{GD}$ = $u_{GS}$ - $u_{DS}$ 中当 $u_{DS}$ 增大到一定程度时，将会使得 $u_{GD}$ = $U_{GS(off)}$ ，此状态就称为预夹断.根据公式可以知道，$u_{GS}$越大，对应的$u_{DS}$也就越大.预夹断轨迹左侧的区域为可变电阻区，该区域中的曲线近似为不同斜率的直线.当$u_{GS}$确定时，直线的斜率被唯一确定，斜率的导数即为d-s间的等效电阻.因而在此区域中，可以通过改变$u_{GS}$的大小来改变等效电阻，因此称为可变电阻区
     2. 恒流区
        恒流区也称饱和区，图中预夹断区域右侧为恒流区.当$u_{GD}$<$u_{GS(off)}$时，各曲线近似为一族平行于横轴的直线.当$u_{DS}$增大时。漏极电流$i_D$仅略有增大，因而可以将$i_D$近似为电压$u_{GS}$控制的电流源，故称为恒流区.利用场效应管做放大电路时，应使其工作在恒流区
     3. 夹断区
        当$u_{GS}$<$u_{GS(off)}$时，导电沟道被夹断，$i_D$≈0，即图中靠近横轴的部分，称为夹断区.一般将使得$i_D$等于某一个很小的电流时的电压$u_{GS}$定义为夹断电压.
     4. 除了上述三个工作区域，当$u_{DS}$增大到一定程度时，漏极电流$i_D$会骤然增大，此时管子将被击穿.由于这种击穿是因栅极-漏极间耗尽层破坏造成的，因而若栅极-漏极之间的击穿电压为$U_{(BR)GD}$,那么漏极-源极的击穿电压$U_{(BR)DS}$ = $U_{GS}$ - $U_{(BR)GD}$，因此当$u_{GS}$增大时，漏极-源极击穿电压将增大
• 2. 转移特性曲线
     转移特性曲线描述当漏极-源极电压$u_{DS}$为常量时，漏极电流$i_D$与栅极-源极电压$u_{GS}$之间的函数关系
     $$\begin{aligned}
     i_D = f(u_{GS})\lvert_{U_{DS} = const}
     \end{aligned}$$
     当场效应管工作在横流区时，由于输出特性曲线可近似为一族平行于横轴的平行线，所以可以用一条转移特性曲线代替恒流区的所有曲线.在输出特性曲线中做横轴的垂线，读出垂线与各曲线的交点坐标值，建立$u_{GS}$、$i_D$坐标系，连接各点所得到的曲线就是转移特性曲线，如下图所示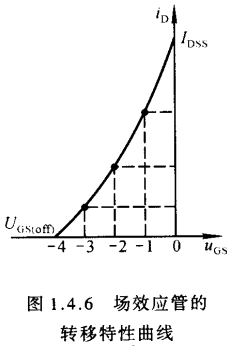
     
     • 根据半导体物理中对场效应管内部载流子的分析可以得到恒流区中$i_D$的近似表达式为
       $$\begin{aligned}
       i_D = I_{DSS}(1- \frac{u_{GS}}{U_{GS(off)}})^2 \qquad (U_{GS(off)}<u_{GS}<0)
       \end{aligned}$$
       上式被称为肖克莱方程
       式中$I_{DSS}$是在$U_{GS}$ = 0V情况下产生预夹断时的漏极电流$I_D$，称为饱和漏极电流
     • 根据前述，当$u_{DS}$增强时，沟道的夹断区将延伸，有效沟道长度将会变短，这将导致$I_D$的增大.沟道长度随着$u_{DS}$增大而变短的现象称为沟道长度调变效应
       考虑沟道长度调变效应后，上式应修正为
       $$\begin{aligned}
       i_D = I_{DSS}(1- \frac{u_{GS}}{U_{GS(off)}})^2(1 + \lvert \lambda u_{DS} \rvert) \qquad (U_{GS(off)}<u_{GS}<0)\end{aligned}$$
       当场效应管工作在可变电阻区时，对于不同的$u_{GS}$，转移特性曲线将有很大的差别.

• 结型场效应管的总结图样
  
  

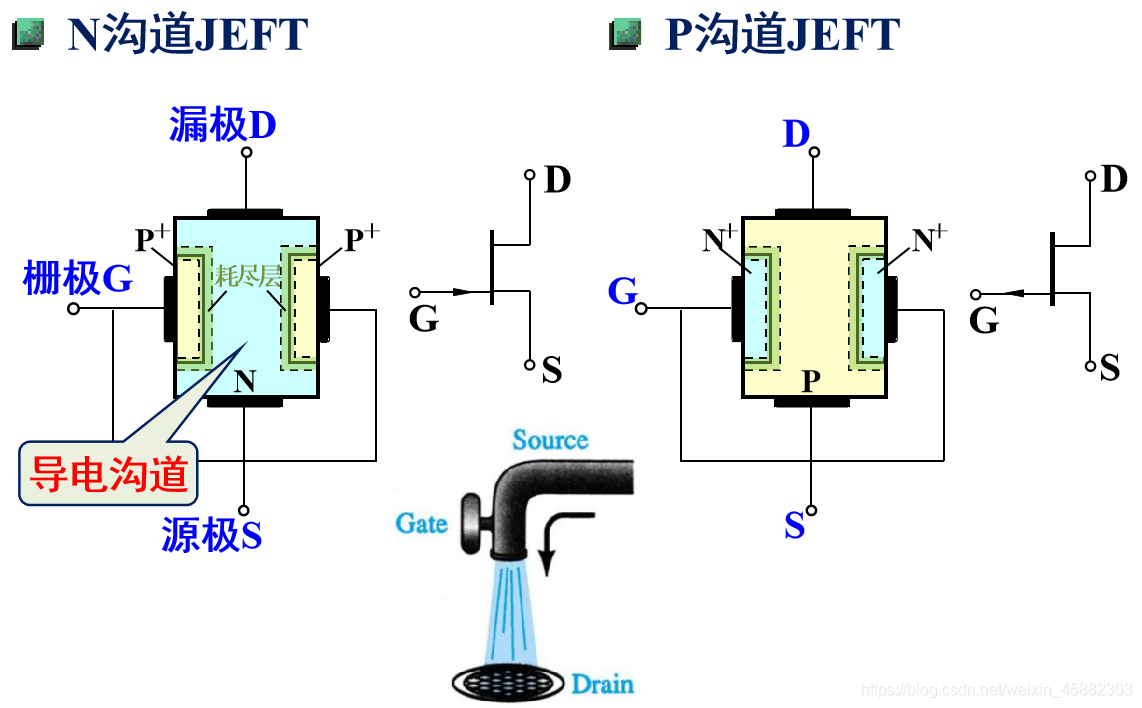
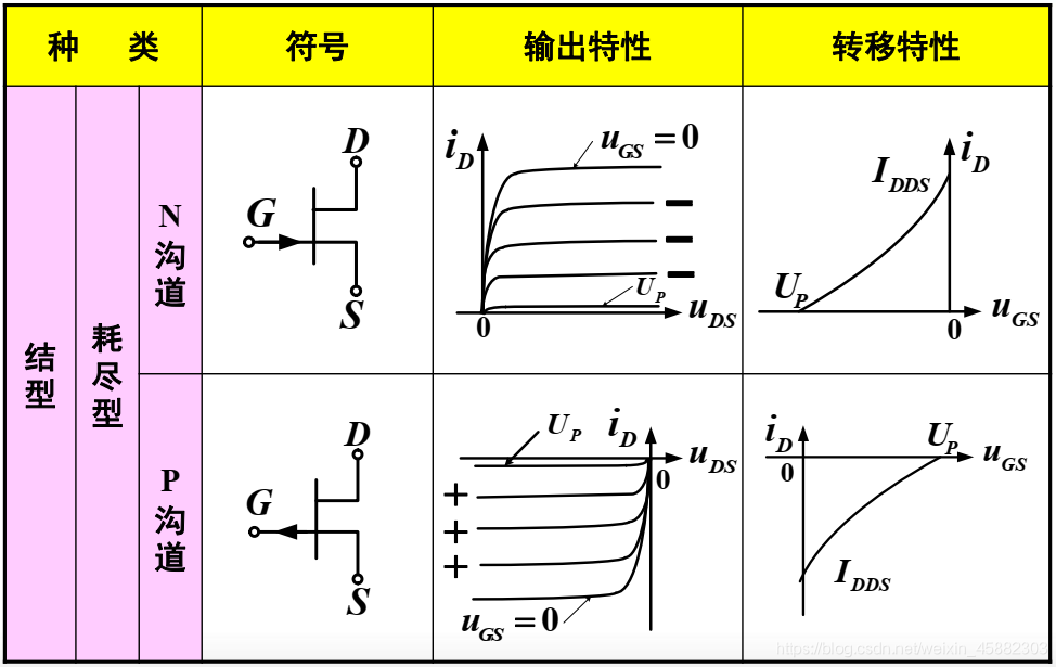
1.4.2绝缘栅型场效应管

绝缘栅型场效应管简介

• 绝缘栅型场效应晶体管的栅极-源极，栅极-漏极之间均采用二氧化硅绝缘层隔离，因此得名.又因栅极为金属铝，故称为MOS管.它的栅极-源极间的电阻比结型场效应管的电阻大得多，可以达到$10^{10} \Omega$以上，并且它比结型产效应管的温度稳定性好、集成化时工艺简单，因而广泛运用在集成电路中.
• 与结型场效应管相同，MOS管也有N沟道和P沟道两类，但每一类又分为增强型和耗尽型两种.凡栅极-源极电压$u_{GS}$为零时漏极电流也为零的管子属于增强型管子，凡栅极-源极电压为零时漏极电流不为零的管子均属于耗尽型管子

N沟道增强型MOS管

• N沟道增强型MOS管结构如图所示，它以一块低掺杂的p型硅片为衬底，利用扩散工艺制作两个高掺杂的$N^+$区，分别引出源极s和漏极d，半导体上制作一层二氧化硅绝缘层，再在二氧化硅绝缘层上制作一层金属铝，引出点击最为栅极g.通常将衬底与源极s连接在一起使用，这样，栅极各衬底各相当于一个极板，中间是绝缘层，形成电容.当栅极-源极电压发生变化时，将会改变衬底靠近绝缘层处感应电荷的多少，从而控制漏极电流的大小.
• 可见MOS管的导电机理与控制电流的原理与结型管均不同
• 
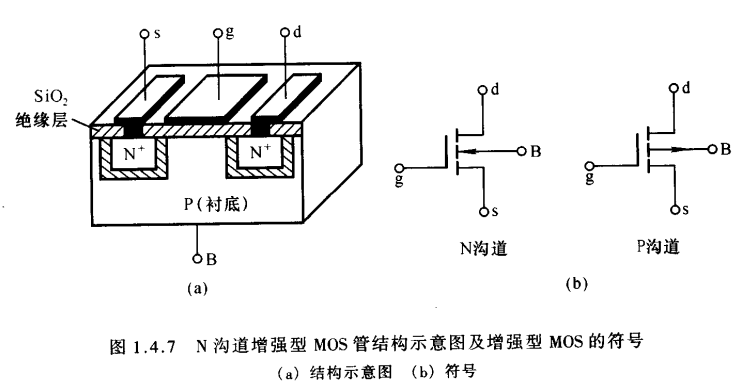
  • 1. 工作原理
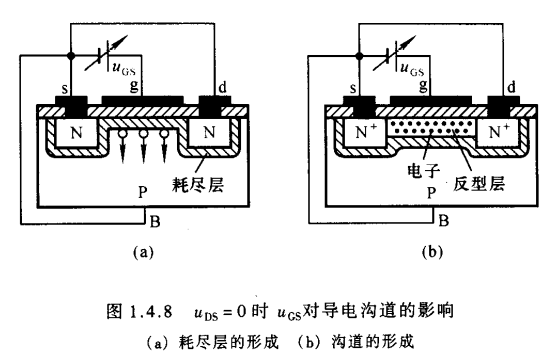
    • 当栅极-源极之间不加载电压时，漏极-源极之间是两只背向的PN结，不存在导电沟道，因此即使漏极-源极间加载电压，也不会有漏极电流
    • 当$u_{DS}$ = 0V 且 $u_{GS}$ > 0V 时，由于二氧化硅的存在，栅极电流为零，但栅极金属层将聚集正电荷，他们排斥P型衬底靠近二氧化硅一侧的空穴，使之剩下不能移动的负离子区，形成耗尽层,如图(a)所示.当$u_{GS}$增大时，一方面耗尽层加宽，另一方面将衬底的自由电子吸引到耗尽层与绝缘层之间，形成一个N型薄层，称为反型层，如图(b)所示.这个反型层就构成了漏极-源极之间的导电沟道.**使沟道刚刚形成的栅极-源极电压称为开启电压$U_{GS(th)}$**，$u_{GS}$越大，反型层越厚，导电沟道电阻越小.
      
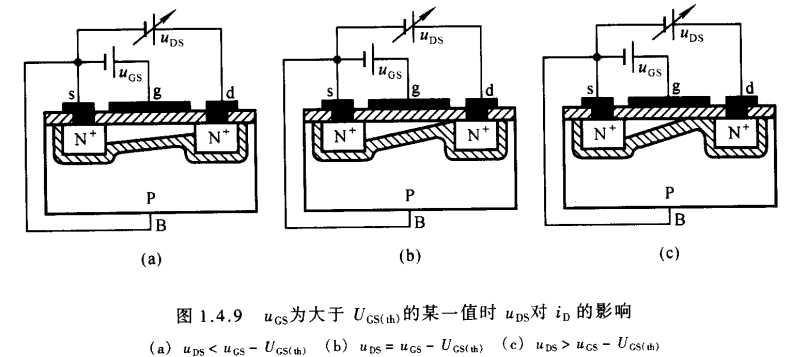
    • 当$u_{GS}$是大于开启电压的一个确定值时，在d-s之间加载正向电压，将产生漏极电流.$u_{DS}$的变化对导电沟道的影响与结型场效应管相似，此处不再赘述.
      
  • 2. 特性曲线与电流方程
       
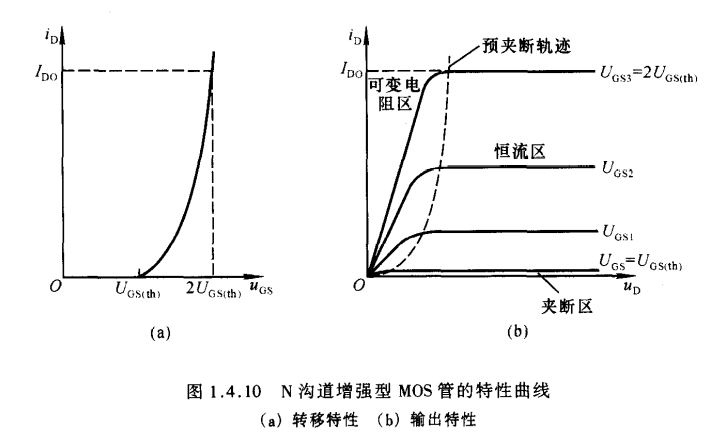
    • 与结型场效应管一样，MOS管也有三个工作区域：可变电阻区、恒流区、夹断区
    • 与结型场效应管类似，$i_D$与$u_{GS}$的近似关系为
      $$\begin{aligned}
      i_D = I_{DO}(\frac{u_{GS}}{U_{GS(th)}} - 1)^2
      \end{aligned}$$
      $I_{DO}$是$u_{GS}$ = 2$U_{GS(th)}$是的漏极电流

N沟道耗尽型MOS管

• 在制造MOS管时，若在绝缘层二氧化硅中掺入大量正离子，使得即使在$u_{GS}$ = 0V 时，在正离子作用下P型衬底表层也存在反型层，即漏极-源极之间存在导电沟道，就会产生漏极电流.
  
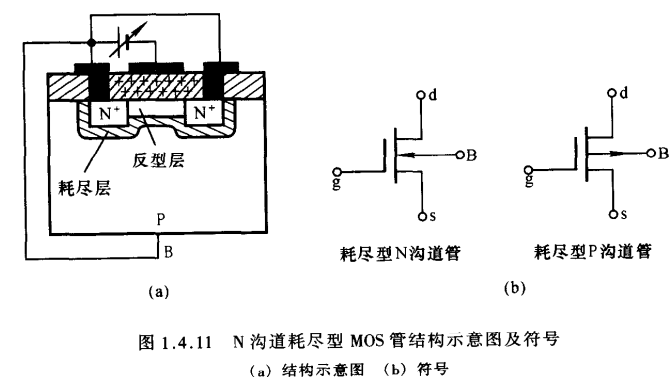
  • 当$u_{GS}$为正向电压时，电压增大，反型层变宽，沟道电阻变小，漏极电流增大；当$u_{GS}$为反向电压时，则相反.此外，当反向电压增大到一定程度时，反型层将消失，漏极-源极之间的导电沟道将消失，漏极电流将不复存在.称此时的电压$u_{GS}$为夹断电压$U_{GS(off)}$.与N沟道结型场效应管相同，N沟道耗尽型MOS管的夹断电压也为负值.

P沟道MOS管

• 与N沟道MOS管相对应，P沟道增强型MOS管开启电压为负值，耗尽型MOS管夹断电压为正值，这一点可以类比N、P型结型场效应管的对应关系.

一波总结

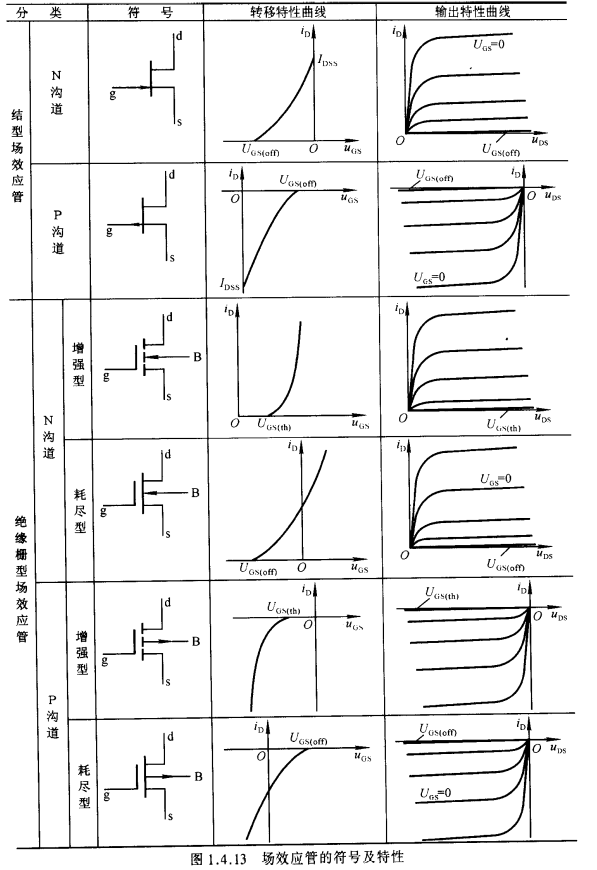
1.4.3场效应管的主要参数

1. 直流参数
   • 开启电压$U_{GS(th)}$
     开启电压$U_{GS(th)}$是增强型MOS管的参数，$U_{GS(th)}$是在$u_{DS}$一定的情况下使得漏极电流存在的最小电压
   • 夹断电压$U_{GS(off)}$
     夹断电压$U_{GS(off)}$是结型场效应管和耗尽型MOS管的参数，$U_{GS(off)}$是在$u_{DS}$为常量的情况下漏极电流达到规定的最小微电流时的$u_{GS}$
   • 饱和漏极电流$I_{DSS}$
     饱和漏极电流$I_{DSS}$是结型场效应管的参数，是在$u_{GS}$ = 0V 时产生预夹断的漏极电流
   • 直流输入电阻$R_{GS(DC)}$
     直流输入电阻$R_{GS(DC)}$是栅极-源极电压与栅极电流之比.
2. 交流参数
   • 低频跨导$g_m$
     $g_m$的数值大小表明栅极-源极电压对漏极电流控制作用的强弱.管子在恒流区且$u_{DS}$为常量的情况下
     $$\begin{aligned}
     g_m = \frac{\Delta i_D}{\Delta u_{GS}}\rvert_{U_{DS} =const}
     \end{aligned}$$
   • 极间电容
     场效应管的三个极之间均存在电容.在高频电路中，应考虑极间电容的影响.
3. 极限参数
   • 最大漏极电流$I_{DM}$
     $I_{DM}$是管子正常工作时漏极电流的上限值
   • 击穿电压
     管子进入恒流区后，使漏极电流骤然增大的$u_{DS}$称为漏极-源极击穿电压
   • 最大耗散功率$P_{DM}$
     $P_{DM}$决定管子允许的温升.$P_{DM}$确定后，便可在管子的输出特性曲线上画出临界最大功耗线.

1.4.4场效应管与晶体管的比较

• 场效应管的栅极-源极电压控制漏极电流，栅极基本不取电流.而晶体管工作时基极总要索取一定的电流.一般在高输入电阻电路中选用场效应管，能够提供一定电流的信号源中选择晶体管.
• 产效应管只有多子参与导电，而晶体管多子少子都参与导电.因少子受环境影响很大，因此在环境条件变化很大的情况下选择场效应管.
• 场效应管的漏极、源极可以互换，互换后变化不大，但晶体管的集电极和发射极互换后差异很大.

1.4.5 MOS管的模型

大信号模型

• 下面以N沟道MOS管为例
  $$
  \left{\begin{aligned}
  I_D = \frac{K^{\prime}W}{L}[(u_{GS} - V_T) - \frac{u_{DS}}{2}]u_{DS} \qquad U_{GS} > V_T
  &\
  I_D = 0 \qquad U_{GS} < V_T
  \end{aligned}
  \right.
  $$
  W、L分别是沟道宽度和沟道长度，$K^{\prime}$叫做跨导参数，它等于载流子的沟道迁移率与单位面积栅电容的乘积，其数值完全取决于工艺
  $$\begin{aligned}
  K^{\prime} = \mu_0 C_0
  \end{aligned}$$
  在临界饱和状态下，满足临界饱和条件
  $$\begin{aligned}
  u_{GD} = u_{GS} - u_{DS} = V_T \Rightarrow
  \
  u_{DS} = u_{GS} - V_T
  \end{aligned}$$
  带入即可得到临界饱和时的电流公式
  $$\begin{aligned}
  I_D = \frac{K^{\prime}W}{2L}(u_{GS} - V_T)^2 = \frac{K^{\prime}W}{2L}u^2_{DS}
  \end{aligned}$$
  考虑沟道长度调变效应后修正为
  $$\begin{aligned}
  I_D = \frac{K^{\prime}W}{2L}(u_{GS} - V_T)^2(1 + \lvert\lambda u_{DS}\rvert) = \frac{K^{\prime}W}{2L}u^2_{DS}(1 + \lvert\lambda u_{DS}\rvert)
  \end{aligned}$$
  为了使得上述公式与结型场效应管公式具有相同的形式，我们可以稍稍变个戏法
  $$\begin{aligned}
  I_D = \frac{K^{\prime}W}{2L}(u_{GS} - V_T)^2
  \ = \frac{K^{\prime}WV^2_T}{2L}(1 - \frac{u_{GS}}{V_T})^2
  \ = I_{DSS}(1- \frac{u_{GS}}{V_T})^2
  \end{aligned}$$
  其中$I_{DSS}$ = $\frac{K^{\prime}WV^2_T}{2L}$，是在栅极-源极电压为零时的漏极电流，这一点与结型场效应管是一致的
  • 强调
    虽然我们是用N型沟道为例进行的推导，但上述公式适用于任何MOS管

    小信号模型

• 漏极视入交流电阻
  $$\begin{aligned}
  r_{ds} = \frac{\Delta V_{DS}}{\Delta I_D} = \frac{1}{\lvert \lambda I_D \rvert}
  \end{aligned}$$
• 跨导
  $$\begin{aligned}
  g_m= \frac{\mathrm{d}I_D}{\mathrm{d}V_{GS}}=(2\frac{K^{\prime}W}{L}\lvert I_D \rvert)^{\frac{1}{2}}
  \end{aligned}$$