半导体基础知识
请注意,本文最近一次更新于:2022-03-12,文章内容可能已经不具有时效性,请谨慎参考
本文最后更新于:2022年3月12日星期六晚上6点26分 +08:00
半导体指常温下导电性能介于导体与绝缘体之间的材料,常见的半导体材料有硅、锗、砷化镓等,硅是各种半导体材料应用中最具有影响力的一种,半导体在集成电路、消费电子、通信系统、光伏发电、照明、大功率电源转换等领域都有应用,如二极管就是采用半导体制作的器件。
1.1.0线性网络常用定理
- 柯希霍夫定律、叠加原理、戴维宁定理、诺顿定理等基础电路知识本章不再赘述,读者若不会或忘却,可自行查阅相关理论,下面只陈述之前未曾涉及的常用定理
米勒定理
- 对于有公共端的线性网络,跨接在A、B两点间的阻抗Z可分别等效为A,B对地的阻抗$Z_A$,$Z_B$
$$\begin{aligned}
Z_A=\frac{Z}{1-\frac{V_B}{V_A}}
\end{aligned}$$
$$\begin{aligned}
Z_B=\frac{Z}{1-\frac{V_A}{V_B}}
\end{aligned}$$
其中$V_A$,$V_B$分别是A和B对地的电压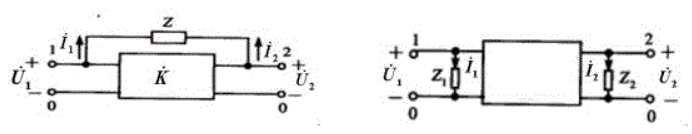
简单证明如下,我们设流入阻抗Z的电流为$I_1$,流入线性网络K的电流为$I_2$
对于左侧图
$$\begin{aligned}
I=I_1+I_2=\frac{U_1-U_2}{Z}+I_2
\end{aligned}$$
对于右侧图
$$\begin{aligned}
I=\frac{U_1}{Z_1}+I_2
\end{aligned}$$
联合得到
$$\begin{aligned}
Z_1=\frac{Z}{1-\frac{U_2}{U_1}}
\end{aligned}$$
同理可以得到$Z_2$米勒对偶定理
- 米勒对偶定理是一个阻抗等效定理
- 在串联回路中,如果一个元件上的电流是输入端电流的K倍,则从输入端视入,该元件的扽报销阻抗也是原值的K倍
- 我们此后在晶体管的讲解中将广泛运用米勒定理的结论
1.1.1本征半导体
- 纯净的具有晶体结构的半导体称为本征半导体
半导体
- 常用的半导体材料为硅和锗,他们均为四价元素.
- 在形成晶体结构的半导体,人为掺杂特定元素时,导电性能具有可控性;并且在光照和辐射条件下,其导电性能还有明显的变化.
本征半导体的晶体结构
- 晶体中的原子在空间中形成排列整齐的点阵,称为晶格
- 相邻原子共用电子,形成共价键
本征半导体中的载流子
- 价电子由于热运动(热激发)获得足够能量后,挣脱共价键的束缚变成自由电子,此时在共价键的位置上形成一个空位置,称作空穴, 空穴带正电.
- 在本征半导体中,自由电子和空穴是成对存在的.
- 若在本征半导体两端加载一外电场,一方面自由电子将产生定向移动,形成电子电流;另一方面,由于空穴存在,价电子将按一定方向依次填补空穴,也就是说空穴也产生定向移动,形成空穴电流.由于空穴和自由电子的带电性质相反,因此两股电流的传导方向相反,本征半导体中的电流是空穴电流和电子电流之和.
- 运载电荷的粒子称为载流子,导体导电中只有自由电子导电;而本征半导体中有两种载流子,即自由电子和空穴均参与导电.
本征半导体中的载流子浓度
- 半导体在热激发下产生的自由电子和空穴对的现象称为本征激发
- 自由电子在运动过程中与空穴相遇就会填补空穴,这种现象称为复合
- 在一定温度下,本征半导体中的载流子浓度是一定的,并且自由电子浓度与空穴浓度相等.
- 本征半导体中的载流子浓度与温度密切相关.温度升高时,半导体中的载流子浓度上升,导电性能增强.温度降低则相反.实验分析表明本征半导体中的载流子浓度是温度的函数:
$$\begin{aligned} n_i = p_i = K_1 T^{\frac{3}{2}}e^{\frac{-E_{CO}}{2kT}} \end{aligned} \tag{1.1.1}$$
式$(1.1.1)$中的$n_i 和 p_i$分别表示自由电子与空穴的浓度($cm^{-3}$),T是热力学温度,k是玻尔兹曼常数($8.63 \times10^{-5} eV/K$),$E_{CO}$为热力学零度时破坏共价键所需的能量,又称为禁带宽度,$K_1$是与半导体材料载流子有效质量、有效能级密度有关的常量.
1.1.2杂质半导体
- 在本征半导体中掺入少量合适的杂质元素,便可以得到杂质半导体
根据掺入杂质元素不同,可以形成N型半导体和P型半导体N型半导体
- 在纯净的硅晶体中掺入五价元素(比如磷),使之取代晶格中硅原子的位置,就形成了N型半导体
- 由于五价原子多出一个价电子,因此,在N型半导体中自由电子的浓度大于空穴浓度,故称自由电子为多数载流子(多子),空穴为少数载流子(少子),由于掺杂原子可以提供多余电子,因此称为施主原子,N型半导体主要靠自由电子导电.
P型半导体
- 在纯净硅中掺杂三价元素(比如硼),使之取代晶格中硅的位置,形成P型半导体.
- 由于三价元素缺少一个价电子,因此在形成共价键的时候就会多出一个空位,当硅原子的价电子前来填补空位时,在原有的共价键处就会形成一个空穴,因此在P型半导体中,空穴是多子,自由电子是少子,P型半导体主要依靠空穴导电.杂志原子称为受主原子
总结
- 对于P、N型杂质半导体,多子的浓度越高,少子的宁都就越低.可以认为,多子浓度约等于所掺杂杂质原子的浓度,因而它受温度的影响很小.而少子是本征激发形成的,所以尽管浓度很低,但是受温度影响很高.
- 一句话就是:多子受温度影响低,少子受温度影响高
1.1.3 PN结
PN结
- 物质总是从浓度高的地方向浓度低的地方扩散,这种由于浓度差产生的运动称为扩散运动
- 当把P型和N型半导体制作在一起时,由于两种类型的半导体主体载流子浓度差别很大,因此会产生扩散运动,从而出现大量复合,在交界面处的多子浓度就会下降.此时在P型半导体中就会出现负离子区,在N型半导体中就会出现正离子区,他们是不能移动的,称为空间电荷区,产生内电场.随着扩散运动的进行,空间电荷区区域加深,内电场增强,方向由N指向P,阻止扩散运动进行.形成的内电场称为内建场
- 由于内建场的存在,在电场力的作用下,载流子产生漂移运动,也即:内建电场是产生漂流运动的原因,在空间电荷区形成后,少子产生漂移运动,空穴从N->P运动,自由电子从P->N运动.
- 在无外加电场的作用下,参与扩散运动的多子数目与少子数目相等,达到动态平衡,形成PN结.此时,空间电荷区域有一定的宽度,电位差为$U_{ho}$,电流为零.
- 理论分析表明,不加外电压时,PN结的内建电动势为:
$$\begin{aligned} \phi_0 = V_t(\frac{N_AN_D}{n^2_i}) \end{aligned}$$
其中$N_A,N_B,n_i$分别是受主浓度,施主浓度和本征浓度
$V_t$是热电势,也就是下面描述PN结电流方程里的$U_T$,二者是一样的:
$$\begin{aligned}
V_t = U_T = \frac{kT}{q}
\end{aligned}$$ - 以后我们取硅PN结的内建势为0.6V,室温下V_t = U_T =26mV*
- 理论分析表明,不加外电压时,PN结的内建电动势为:
- 当P、N型半导体内的杂志浓度相等时,形成的空间电荷区在两端是对称的,也称为对称结,杂质浓度不相等时称为不对称PN结,两种PN结的外部性质相同.
- 绝大部分空间电荷区内的空穴和自由电子都非常少,因此在分析PN结特性时常忽略载流子的作用,而只考虑离子区的电荷,这种方法称为耗尽层近似,因此空间电荷区也称为耗尽层
PN结的单向导电性
- PN结两端外加电压时就会破坏原来的平衡状态,此时扩散电流就不再等于漂移电流.当外加电压极性不同时,PN结会表现出不同的导电性能,即呈现出单向导通性.
- PN结外加正向电压处于导通状态
- 当电源正极或者正极串联电阻后连接到PN结的P端,且电源负极或负极串联电阻后接到PN结的N端时,称PN结外加正向电压,也称正向接法或正向偏置.
- 此时外加电场将多数载流子推向空间电荷区,使空间电荷区变窄,削弱内电场,破坏原来平衡,使得扩散运动加剧,漂移运动削弱,从而形成正向电流,PN结导通.
- PN结外加反向电压时处于截止状态
- 当电源正极或者正极串联电阻后连接到PN结的N端,且电源负极或负极串联电阻后接到PN结的P端时,称PN结外加反向电压,也称反向接法或反向偏置.
- 外加电场使得空间电荷区变宽,加强内电场,阻止扩散运动进行,加剧漂移运动进行,形成反向电流,也称漂移电流
- 由于少子的数目极少,因此形成的反向电流很小,在分析时常常忽略不计,因此外反向电压时PN结处于截止状态.
PN结的电流方程
- 理论分析可以得到,PN结两端所加电压u与流过它的电流i的关系为:
$$\begin{aligned} i = I_S(e^{\frac{qu}{kT}} - 1) \end{aligned} \tag{1.1.2}$$
式$(1.1.2)$中$I_S$为反向饱和电流,q为元电荷(即电子的电量),k为玻尔兹曼常数,T为热力学温度. - 定义$U_T = \frac{kT}{q}$,那么:
$$\begin{aligned} i = I_S(e^{\frac{u}{U_T}} - 1) \end{aligned} \tag{1.1.3}$$
PN结的伏安特性
- 根据$(1.1.3)$,当PN结外加载正向电压,并且u >> $U_T$时,i ≈ $I_S(e^{\frac{u}{U_T}} )$,即i随u按照指数规律变化;当PN结加载反向电压,并且数值上u >> $U_T$时,i ≈ -$I_S$.
- 当反向电压超过一定数值时,反向电流急剧增加,称之为反向击穿.
- 击穿按照机理分为齐纳击穿和雪崩击穿两种情况
- 齐纳击穿
在高掺杂的情况下,由于耗尽层的宽度很窄,不大的反向电压就可以在耗尽层形成很强的电场,可以直接破坏共价键,使得价电子脱离共价键约束,产生电子-空穴对,致使电流急剧增大,这种击穿称作齐纳击穿.- 关于高掺杂情况下耗尽层宽度变窄而不是边宽的解释:
在高掺杂情况下,自由电子或空穴的浓度增大,因此扩散作用会增强,由此产生的内建电场强度会增大,耗尽层电压$U_{ho}$会增强,此时势垒电压会增大.但场强正相关于浓度,而势垒电压正向关于浓度的自然对数,根据U = Ed 可知间距会变窄.
- 关于高掺杂情况下耗尽层宽度变窄而不是边宽的解释:
- 雪崩击穿
在掺杂程度不大的情况下,耗尽层的宽度较宽,低反向电压无法产生齐纳击穿,而当反向电压增大到一定程度时,耗尽层内的电场使得少子加快漂移速度,从而在与共价键中的电子相碰撞过程中将价电子撞出共价键,产生空穴-自由电子对. 这样的过程是级联的,因为新产生的自由电子与空穴又参与撞击,致使电流急剧增加,这种击穿称为雪崩击穿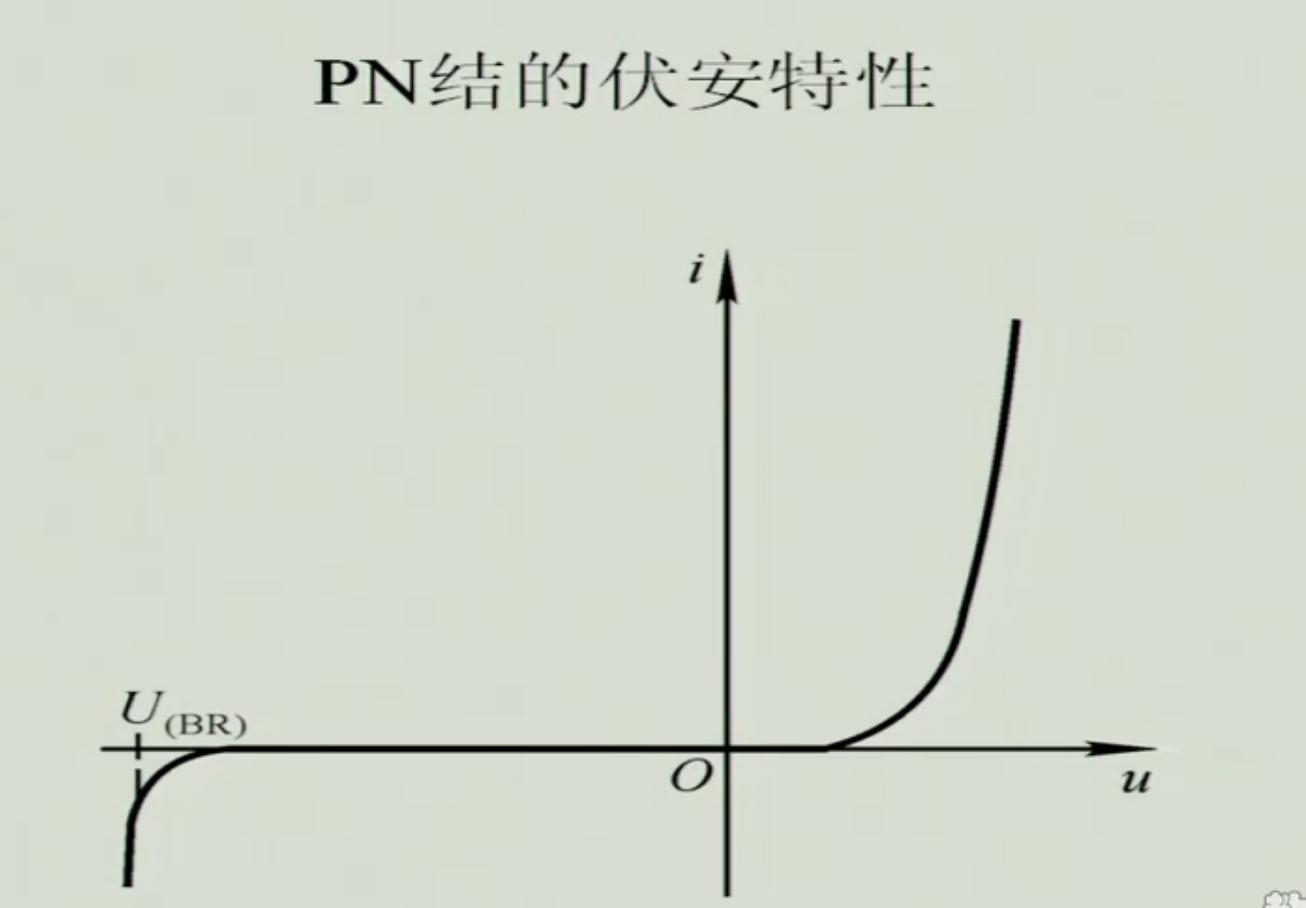
- 齐纳击穿
- 击穿按照机理分为齐纳击穿和雪崩击穿两种情况
PN结的电容效应
- 在一定条件下,PN结具有电容效应,根据产生的原因不同可以将其分为势垒电容和扩散电容
- 势垒电容
- 当加载在PN结两端的电压变化时,空间电荷区域的宽度会随之发生变化. .
- 耗尽层宽窄变化所引起的等效电容称之为**势垒电容$C_b$**,$C_b$具有非线性性,它与结面积、耗尽层深度、半导体介电常数以及外加电压有关.
- 势垒电容$C_b$由下述式子表示:
$$\begin{aligned}
C_b = \frac{C_{b0}}{(1-\frac{V_D}{\varphi_0})^m}
\end{aligned}$$
式中$\varphi_0$是内建势,m是常数(一般为1/3~1/2),$V_D$是结电压,正偏为正,反偏为负,$C_{b0}$是在结电压为0时的势垒电容.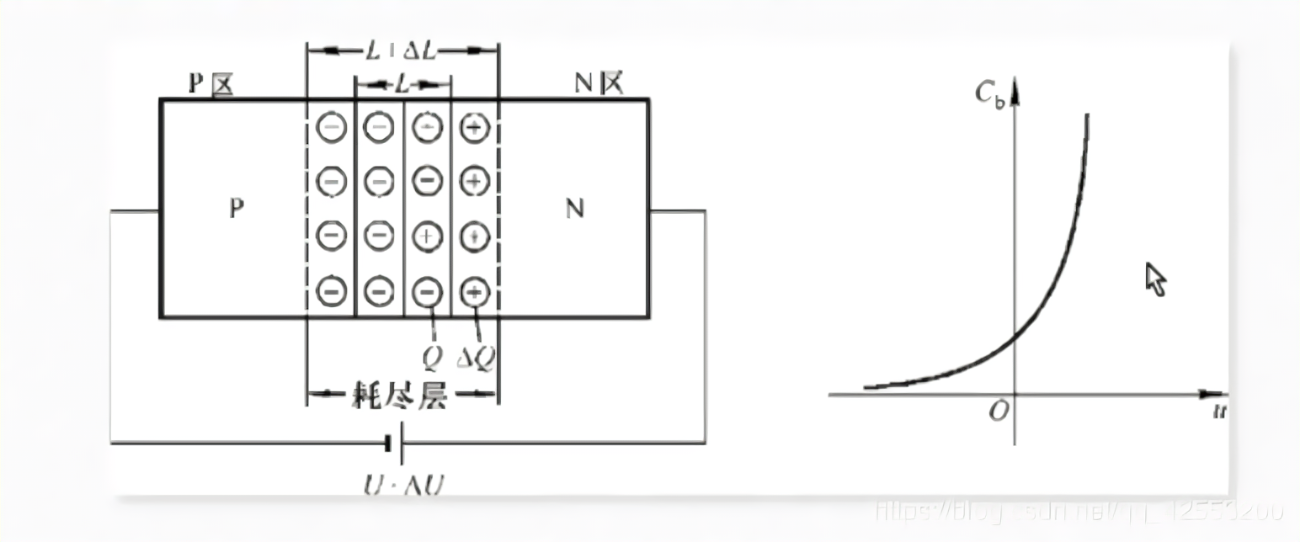
- 扩散电容
- PN结处于平衡状态时的少子常称为平衡少子.PN结处于正向偏置时,从P扩散到N的空穴和从N扩散到P的自由电子称为非平衡少子.
- 在外加电压一定时,靠近耗尽区表面的地方非平衡少子的浓度高,而远离交界面的地方浓度低,并且浓度自高到低逐渐衰减到零,形成一定的浓度梯度,于是会形成扩散电流.当外加正向电压增大时,非平衡少子浓度增大并且浓度梯度也增大,因此扩散电流(正向电流)增大,反之相反.
- 扩散区内电荷的积累与释放与电容器充放电过程相同,这种电容效应称为扩散电容$C_d$.扩散电容具有非线性性,其与流过PN结的正向电流i、温度的电压当量$U_T(即\frac{kT}{q})$、非平衡少子的寿命$\tau$有关.
- $C_d = \alpha I_D$,可见反偏时扩散电容为零.
- 势垒电容
- 由此可见,PN结的电容$C_j是C_b与C_d之和$,低频信号时容抗很大,所以其作用可以忽略不计,因此我们只有在高频信号时才考虑结电容的作用.
您阅读这篇文章共花了:

Invitation
Floral-Sunsunrise
FeynmanDirac
created:12/03/2022
Welcome to Floral-Sunsunrise
This is an identification card as an honored membership of FeynmanDirac
Happy to see you follow FeynmanDirac, enjoy science together
 验证码启动中...
验证码启动中...
备用人机验证